Discussion:Gravitation

Évaluation de l’article « Gravitation »

Avancement	Importance	pour le projet
Bon début	Maximum		Astronomie (discussion • critères • liste • stats • hist. • comité • stats vues)
			Astronomie fondamentale (discussion • critères • liste • stats • hist. • comité • stats vues)
			Cosmologie (discussion • critères • liste • stats • hist. • comité • stats vues)
			Physique (discussion • critères • liste • stats • hist. • comité • stats vues)
			Sciences (discussion • critères • liste • stats • hist. • comité • stats vues)
	Élevée		Sélection francophone (discussion • critères • liste • stats • hist. • comité • stats vues)
	Moyenne		Sélection transversale (discussion • critères • liste • stats • hist. • comité • stats vues)

supp §

les 2 derniers paragraphes sont à supprimer.Utilisateur:Yves

les paragraphes supprimés au cas où:

Ce qui avait intrigué Einstein, et même Newton, dans l'interprétation mécanique de la gravitation, est que cette force paraissait "intelligente". En effet, qu'un objet 2 fois plus massif qu'un autre puisse tomber à la même vitesse impliquait que la force établie entre la Terre et les objets pesants était capable de s'adapter au travail à fournir. En effet, si vous devez par exemple pousser un chariot de 50kg à 10km/h sur une distance de 10m, il paraît évident que vous devrez exercer sur le chariot une force 5 fois plus grande que si votre chariot avait une masse de 10kg. Mais nous dirons que êtes en mesure d'ajuster votre force de poussée parce que vous êtes pensant et que votre cerveau calcule l'intensité des forces à appliquer dans les deux cas afin de faire rouler ces deux chariots à la même vitesse.

Attention à ne pas inverser cause en conséquence : nos équations mathématiques ne sont qu'une logique plaquée sur des observations de la Nature (qui n'en a rien à faire !) ... Revoir Kant
Laurent 5 jun 2003 ・10:34 (CEST)

Je ne conteste pas le retrait, mais pourait-on donner une petite justification?

Je pense surtout qu'il faudrait dire quelque mots sur l'égalité entre masses d'inertie et masse gravitationnelles.

-- Looxix 5 jun 2003 ・22:35 (CEST)

Je suis l'auteur de ces deux paragraphes, je ne comprends pas leur suppression. Ils mériteraient certainement d'être développés mais il est tout aussi interressant de connaître le mécanisme de pensée qui amène à une découverte fabuleuse que la découverte en soi-même. -- DavidP

Ils mériteraient surtout d'être éclaircits.

En fait je ne comprend pas vraiment ce qu'il veulent dire, par exemple: ... cette force paraissait "intelligente"; n'est-ce pas le cas de toute les forces et de toute les lois physique? Elles tombent toutes pil-poil avec les équations! -- Looxix 9 jun 2003 ・18:26 (CEST) Autre concept (relire Kant) : les équations mathématiques sont des approches logiques, dont la Nature se moque totalement, plaquées sur des phénomènes observés ! GMC 25/11/2010

Eclaircis au minimum. Ils me parraissent bien confus et source de confusion supplémentaire. Il est vria que le sujet des interrogations sur masse inertielle et masse gravitationnelle est un peu difficile, mais c'est le lieu pour travailler le sujet. Ploum's 9 fév 2004 à 03:11 (CET)

The curvature of spacetime - image

New image was added to Commons:

The curvature of spacetime around the source of the gravitational force

Superborsuk

2 articles quasi identiques

Ou du moins qui se ressemnlent fortement au début, et sont complémentaires par la suite. Est-il vraiment nécessaire de faire 2 articles entre gravitation et Loi universelle de la gravitation ? Rhadamante 19 juillet 2006 à 22:15 (CEST)

Je crois que l'article Loi universelle de la gravitation devrait être renommé Loi universelle de la gravitation de Newton comme c'est le cas de l'article anglophone. --Le Père Odin 3 novembre 2007 à 16:15 (CET)

Ajout de la pomme de Newton

J'ai voulu ajouter le coup de la pomme de Newton afin que le commun des mortels comprenne pourquoi la vitesse de chute d'un corps ne dépend pas de sa masse (disons: son poids). Merci de ne pas m'en vouloir d'avoir mégoté sur les détails: le vide, l'interaction pomme-pomme, l'uniformité spatiale de la gravitation dans le domaine de l'expérience, etc..Il reste à expliquer que la pomme et la boule de pétanque chutent à la même vitesse : il faudrait citer Newton qui disait déjà que c'était le cas dans la mesure où toutes les choses de ce monde sont faites de la même substance, Einstein précisant ensuite que cette substance s'appelle "énergie". Sauf erreur de ma part.

Ne pourrait-on utiliser la progression historique de la compréhension intellectuelle de la gravitation afin de rendre l'article plus lisible ? Par exemple en utilisant des références telles que "Galilée et Newton lus par Einstein" de F Balibar. Et introduire le formalisme mathématique dans un deuxième temps.

LyricV 10 février 2007 à 16:40 (CET)LyricV

Remodelage de l'article ?

Après avoir ajouté la comparaison de la chute d'une pomme et d'une boule de pétanque, je me propose de remodeler quelque peu l'ensemble de l'article, en reprenant le maximum de choses dans ce qui est déja écrit :

sommaire:

1. Compréhension intuitive. Où je mettrai ce que j'ai déja écrit, principalement.
2. La modélisation de Galileo Galilei. Où j'expliquerai sa modélisation .
3. La modélisation de Newton. Où j'expliquerai...
4. La modélisation de Lagrange et Hamilton. Où j'expliquerai leurs apports.
5. La modélisation d'Einstein. Où j'expliquerai le moins possible, car c'est le sujet de l'article Relativité générale.
6. Articles connexes.
7. Bibliographie.

Je me rends compte que je ne sais pas comment modifier le sommaire !

Cette difficulté mise à part, voilà mon programme, ai-je l'accord de tout le monde ?

LyricV 11 février 2007 à 10:30 (CET)

Pourquoi pas ! Mais le terme modélisation me gêne un peu... Quant au sommaire, il est généré automatiquement : c'est le reflet des titres utilisés dans le corps de l'article.--Manu (discuter) 11 février 2007 à 13:19 (CET)

Que j'explique un peu ma démarche:

1. j'ai observé que de nombreuses personnes ne comprennent absolument pas pourquoi les objets devraient tomber tous à la même vitesse dans le vide, il m'a semblé important de l'expliquer sans équation au commun des mortels qui espère trouver rapidement une justification compréhensible (c'est une encyclo grand public, non ?), pour ensuite avancer un peu plus dans les détails .
2. Expliquer aussi pourquoi il y a des masses m et m' dans la loi de Newton, et simplement ce qu'est ce principe d'équivalence (déja à l'époque de Newton avant d'aller voir Einstein) me parait plus important que d'exposer des lois connues et incompréhensibles, et des raisonnements parfaitements rigoureux (j'espère ne pas avoir mis de contre-vérité quand même!).
3. L'exposé de la chronologie des idées me parait important pour la compréhension progressive du néophyte. Maintenant, dans l'état où je laisse l'article, il y a des redondances avec histoire de la gravitation, mais peut-on vraiment séparer les deux ?

LyricV 19 février 2007 à 13:48 (CET)

Tu es sympa LeYaYa de modifier ce texte sans en parler ici ! Ce que tu as enlevé est important et nullement confus, peut-être n'es-tu pas d'accord, peut-être que tu n'en vois pas l'interêt (peut-être que tu n'as pas pris le temps de lire et de comprendre!) J'ai bien cogité sur cet article, et je n'ai pas de bonne raison (même pas de modestie face à toi) pour te céder sur ce sujet. Applique à toi-même tes bonnes idées : propose les modifs dans ton espace personnel, jusqu'à ce que les autres trouvent ça acceptable !LyricV 20 février 2007 à 04:24 (CET)

salut LyricV. D'une je me suis contenté de mettre en commentaire, je n'ai pas effacé. Par ailleurs j'ai expliqué pourquoi je le faisais dans le commentaire associé à ma modification, et tu l'as lue. On n'est pas obligé non plus de mettre un roman pour chaque modif! Ta comparaison n'a pas de sens, on fait des modifs dans son espace perso quand on veut reprendre une grande partie d'un article ou qu'on veut écrire une partie particulièrement compliquée. Je ne vais pas te faire une exégèse ici de l'utilisation appropriée de l'espace perso. Maintenant je prétend que ta phrase n'avait pas grand sens, point, je ne comprend pas ce qu'elle veut dire alors je la vire car je pars du principe que si quelqu'un d'un peu familier avec la RG (moi) ne comprend pas cette phrase alors le lecteur lambda soit ne comprendra rien, soit sera induit en erreur. Désolé si cela ne te fait pas plaisir. Bien cordialement, LeYaYa 20 février 2007 à 08:54 (CET)

Je suis d'accord avec LeYaYa sur le fond : la phrase n'est pas claire et je ne la comprends pas non plus. D'un côté tu dis que "La Relativité Générale nous a apprit que seul le paramètre énergie des corps rentre en compte dans la gravitation", et de l'autre tu dis "ce n'est pas la quantité (d'énergie) qui détermine la vitesse de chute d'un corps vers la terre". Selon ma compréhension de la RG (mais je ne suis pas expert), la première phrase est vraie, mais la seconde est fausse. Ce qui détermine la vitesse de chute d'un corps vers la terre est la quantité d'énergie de la terre, vis à vis de laquelle la quantité d'énergie des "micro-briques" est négligeable. En conséquence, toutes les micro-briques, et la brique, suivent la même géodésique dans l'espace-temps déformé par la terre (la brique ne déformant elle qu'insensiblement l'espace-temps). --Jean-Christophe BENOIST 20 février 2007 à 10:12 (CET)

Salut à tous. Je suis content de trouver l'occasion de vous (ré)expliquer ma pensée.

Déja à JC BENOIST:

• oui le tenseur de courbure n'est influencé que par le tenseur énergie totale du corps; je n'ai pas pris la place pour expliquer que la quantité d'nrj de la terre détermine la gravitation car je ne parlais que de celle du corps en chute (ne pas faire trop long m'a-t-on dit: LeYaYa peut-être. Et puis Mr Lambda pense surtout au poids de l'objet en chute quand il pense comme Aristote que...) et il est exacte que la quantité d'nrj de l'objet n'intervient pas dans sa chute dans un champ de gravitation uniforme, tu le sais chaque "micro-brique" suit sa géodésique (et son influence est négligée).
• Il est exacte (mais détrompe moi) que chaque corps n'existe que par son (tenseur) nrj (avec composante électro et étendue spaciale) en RG, et j'ai utilisé cette réduction à l'nrj dans la RG pour finir d'expliquer qu'il n'y a pas de qualité qui puisse distinguer les "micro-briques" les unes des autres pour la gravitation. Quand à la quantité d'nrj, elle se répartit uniformement (aller, on néglige la rotation de l'objet sur lui-même et autres petits trucs!) sur des "micro-micro-briques" s'il le faut, même l'nrj cinétique se réparit au passage. Donc sans parler de géodésique, on peut faire comprendre l'indépendence de la chute par rapport au poids et à la nature de l'objet.

A LeYaYa : Merci d'engager la conversation qlq part. Ce que je viens d'écrire à JC t'explique peut-être un peu ? Si ce que tu as enlevé de l'article ne doit plus y revenir, car incompris par plusieurs, alors il faut enlever le reste de la 1ère partie qui sinon est ridicule.

LyricV 20 février 2007 à 11:57 (CET)

je pense que c'est une mauvaise idee de parler de relativite generale dans ce paragraphe qui parle de la vision newtonienne de la gravitation. En RG il n'y a pas de force de gravitation. LeYaYa 20 février 2007 à 13:53 (CET)

Rappel : il s'agit du paragraphe didactique pour nos contemporains, toute connaissance moderne y a sa place, y compris l'approximation newtonnienne dont le vocabulaire de base (et intuitif) est partagé par tous les Mr et Mme Lambda (ou presque). Tu ne dis rien de plus sur mes explications ? LyricV 20 février 2007 à 20:01 (CET)

ce n'est pas une question d'avoir sa place ou pas, ton explication est mauvaise, point. Le fait que les corps tombent a la meme vitesse n'a rien a voir avec le fait que la terre ait une energie BEAUCOUP plus grande que celle des objets de la vie courante, c'est un resultat strictement exact. Ce n'est pas parce que tu as un bon objectif et que tu mets des efforts dans ce paragraphe que tu vas y arriver necessairement. Quand je lis ca je n'ai pas la patience de donner des commentaires sur le reste desole. LeYaYa 21 février 2007 à 10:07 (CET)

Euh, là je me sens concerné. C'est peut-être à la suite de remarques que j'avais faites (auxquelles tu n'as pas réagi) que Lyric a écrit cela. L'égalité de la masse pesante et de la masse inerte est effectivement stricte, et c'est ce que dit le principe d'équivalence. Mais cela n'aboutit à l'égalité (stricte) des vitesses de chute que dans le cadre de la physique newtonienne (en tout cas, avec les formules de la physique newtonienne), où les "m" se simplifient. Je ne suis vraiment pas sûr que la vitesse de chute d'un trou noir de la masse de la terre sur la terre sera strictement égale à la vitesse de chute d'une bille de diamètre équivalent sur la terre. L'espace-temps est déformé de manière complètement différente dans un cas et dans l'autre, aboutissant à des géodésiques différentes. Cela ne remet pas en cause, à mon sens, le principe d'équivalence qui stipule dans le fond qu'aucune expérience ne peut distinguer un référentiel accéléré d'un champ de gravitation uniforme, et c'est sans aucun doute le cas pour la bille "trou noir" aussi (probablement car dans le référentiel accéléré de la bille "trou noir" le temps est distendu, et que dans ce référentiel, on calcule la même vitesse de chute que la bille normale). Telle est ma compréhension, mais il se peut que quelque-chose m'échappe, et je te fais confiance LeYaYa si tu dis que tel est lecas. Mais peut-être s'est-on mal compris ? Ce serait intéressant d'en discuter et de se convaincre en tout cas. --Jean-Christophe BENOIST 21 février 2007 à 14:07 (CET)

on peut essayer de discuter de choses compliquees par ailleurs, mais pour rester dans le sujet et faire bref, je persiste a dire que ce n'est pas en parlant de RG dans ce paragraphe qu'on va eclaircir ce qui se passe dans la tete de quelqu'un qui ne comprend pas pourquoi les corps tombent a la meme vitesse. Bien cordialement, LeYaYa 21 février 2007 à 14:25 (CET)

D'accord, le paragraphe conclusif de l'expérience de pensée, bien que non-faux (?), n'apporte rien de clair, au contraire, quelle que soit sa version. Ce n'est pas moi qui le supprimerais, mais je ne m'y oppose pas. Cela dit, j'aimerais bien connaitre le fin-mot de l'histoire, on discute "des choses compliquées" ici, sur ta page de discussion, ou tu n'as peut-être pas envie ? --Jean-Christophe BENOIST 21 février 2007 à 17:35 (CET)

Compréhension intuitive

Voilà, j'ai relu le premier paragraphe et vos diverses discussions. J'ai essayé dans mes modifs une conciliation des divers points de vue. Cela ne préjuge en rien d'une discussion plus avancée sur la place de ce paragraphe et son articulation avec le reste de l'article. J'ai mis quelques phrases superflues en commentaires. Dites moi ce que vous en pensez. Cordialement, Kropotkine 20 février 2007 à 21:40 (CET)

Pas satisfait, pas content, mais je ne bataillerai pas bêtement: vous devriez lire et prendre la peine de réfléchir à mes explications ci-dessus. LyricV 20 février 2007 à 22:10 (CET)

Je suis revenu voir ce qu'était devenu la gravitation sur Wikipedia depuis 2003. Je m'aperçois qu'il y a eu un sacré coup de balai sur le travail des premiers auteurs le 19 février 2007. Je trouve cela très dommageable à l'esprit du travail collectif. Sur le fond, l'article ressemble maintenant à un vrai charabia scientiste inaccessible au commun des mortels, c'est bien dommage et surtout je pense que c'est une dérive. En tant qu'enseignant je me permets de tester les articles auprès de mes élèves, et là ils ouvrent des grands yeux. DavidP 21 mars 2007 à 21:17 (CET)

Il y aura peut être un jour un grand coup de balai sur l'article actuel... Tout n'est pas à jeter dans le travail de Lyric, même si globalement je n'approuve pas trop non plus. En attendant, rien n'empêche de corriger, de récupérer du travail antérieur, voire de réverter.. Je n'en ai pas le courage et la gravitation n'est pas ma spécialité. Mais vous.. peut-être ? --Jean-Christophe BENOIST 21 mars 2007 à 21:46 (CET)

Bonjour JC. Bien sûr que tout n'est pas à jeter, loin de moi cette idée. Par contre c'est ce qui a été fait le 19 février. J'utilisais cet article auprès de mes élèves (en leur indiquant l'adresse web de wikipedia). Moi non plus je ne me sens pas à refondre tout çà ! Tout simplement parce que la première version qui a vécu 5 ans était une oeuvre collective dans l'esprit wiki. Il faudrait reconstituer un groupe sur cet article.DavidP 22 mars 2007 à 20:11 (CET)

Modifications d'Emmanuel

Bonjour Emmanuel. Que je te dise : que la gravitation soit due à la masse est difficile à comprendre. En effet : de quelle masse parles-tu ? En lisant l'article, un lecteur comprendra l'ambiguité de cette définition, par contre la def sans la masse est parfaitement correcte et neutre de ce point de vue; quand à la connaissance qui n'est pas encyclopédique, l'article (de cette encyclopédie qu'est WP) explique pourquoi la masse (les masses gravifique et inertielle) est importante dans cette force (et il est dit dans l'article qu'en RG ce n'est plus la masse qui compte, mais l'énergie totale).

Pour ton expérience avec les boules de papier et de métal : si c'était vrai, même Aristote l'aurait vu ! (résouds les équations, si tu veux !)S'il te plait enlève ça ! Cordialement.LyricV 28 mars 2007 à 21:44 (CEST)

La def sans masse est effectivement correcte (quoique, voir ce qui suit), mais je la trouve encore plus piègeante que la définition avec ! En fait la définition sans masse est assez subtile : la première fois que je l'ai lue, j'ai froncé les sourcils, la deuxième je me suis dit : ah.. OK. La subtilité et l'important est dans le mot quelconque, mais je suis sûr que 90% des lecteurs ne verront pas la subtilité. A la rigueur, au moins mettre "quelconque" en italique. Mais je vois ce que tu veux dire, Lyric ; tu fais sans doute référence aux solutions "sans masse" des équations d'Einstein (Univers de de Sitter) et au fait que l'énergie peut également déformer l'espace-temps. Mais dans la définition, il est bien question de corps, et donc nous ne sommes pas dans un univers de de Sitter, ou en présence d'énergie. Dans ce contexte, la notion de masse est sans ambiguité. En fait, si on veut une définition vraiment "neutre" de la gravitation, on ne devrait même pas parler de "corps". --Jean-Christophe BENOIST 28 mars 2007 à 23:03 (CEST)

En fait, ce qui me gène dans la définition avec masse, c'est qu'elle propose dès le début de l'article une cause déterminée pour la gravitation, alors que j'ai essayé de montrer dans l'article que cette cause n'est pas évidente, et ne l'a été pour aucun scientifique, et même n'est plus la véritable cause depuis Einstein. Parler de corps est important car c'est une donnée intuitive accessible à tout lecteur, la masse c'est floue, ambigue tant que l'on en a pas parlé précisement. Par contre, on ne peut pas garder l'erreur des boules de papier et de métal : les équations de Newton parlent d'elles-mêmes ! Bon, je vais aller voir les univers de Sitter un de ces jours (déja que je trouve l'univers d'Einstein costaud !) LyricV 28 mars 2007 à 23:43 (CEST)

ok--Manu (discuter) 29 mars 2007 à 22:01 (CEST)

Tu tiens au mot "masse" ? LyricV 29 mars 2007 à 22:05 (CEST)

j'ai remis l'expérience avec les précautions qui s'impose car je trouve qu'elle met l'intution en défaut très simplement--Manu (discuter) 29 mars 2007 à 22:15 (CEST)

Au moins, je ne suis pas convaincu qu'elle soit présentée ou il faut ni clairement avec les précautions qu'il faut : il faut mettre en gros les pb qui apparaissent si la hauteur de chute est plus grande, sinon un lecteur non averti ne comprendra rien aux génies de galilée et Newton. Mais, je n'y suis pas plus favorable. LyricV 29 mars 2007 à 22:25 (CEST)

je ne comprend pas bien : que proposes-tu ?--Manu (discuter) 29 mars 2007 à 22:33 (CEST)

Vois ma modif. Es-tu bien sûr que la différence de temps de chute n'est pas perceptible dans le cas de ton expérience ? LyricV 29 mars 2007 à 22:46 (CEST)

Constate par toi même !! Ceci dit, très belle reformulation --Manu (discuter) 29 mars 2007 à 22:48 (CEST)

Il manque...

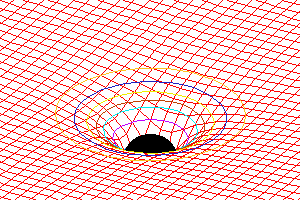
Je prends par exemple la section concernant "La modélisation d'Albert Einstein" : Après avoir énoncé la théorie de la relativité restreinte en 1905, Einstein cherche à la rendre compatible avec la gravitation dont la force se propage à une vitesse infinie alors que la vitesse de la lumière est la vitesse maximale pour la relativité restreinte. Vers 1915, la solution viendra de l'utilisation d'un espace-temps courbé, de la relativité galiléenne et de la notion d'énergie. Sa théorie porte le nom de Relativité Générale, et la théorie newtonienne en est une approximation. Simplification en quelques mots: par son énergie, chaque corps déforme l'espace et le temps (ou plutôt l'espace-temps) qui l'environne, y compris le chemin respectant le principe de moindre action pour aller d'un point à un autre. Cette déformation se manifeste, entre autres, par la gravitation. En gros, il manque des références (articles de science d'Einstein ou plutôt un livre d'Histoire des sciences traitant du sujet, je dois en avoir un d'ailleurs quelque part...), une illustration (il y en a une en page de discussion), la formulation est obscure pour le profane (qui ne connait pas forcément le principe de moindre action => expliquer un peu plus longuement ce point), et surtout il manque les traits essentiels de la théorie d'Einstein qui révolutionne ce domaine de la physique, comme par exemple la géométrisation de la notion de "gravitation", il en découle l'absence de notion de "force de gravitation" qui est remplacée par une déformation d'un "tenseur" espace-temps, le principe d'équivalence qui rend le concept de "gravitation" équivalent à un terme d'accélération dans les équations d'Einstein (Exemple célèbre d'un homme dans un ascenseur en chute libre, équivalent à un homme soumis à un champ de gravitation), dire aussi que cela explique aussi pourquoi la masse "grave" est équivalente à la masse "inertielle"... Bref on saisit pas bien dans la version actuelle en quoi la modélisation d'Einstein est importante. En lien avec la section suivante, il manque aussi en quoi l'interaction gravitationnelle vue par Einstein est différente des 3 autres interactions fondamentale, en gros pourquoi on n'arrive pas à avoir une théorie du tout pour l'instant (réponse partielle : théorie non renormalisable). Il manque aussi des détails tel que l'éthymologie du mot, dire qu'on est passé des termes "force de gravitation" à "champ gravitationnel", et à "interaction gravitationelle", dans la liste des théories gravitationnelles quantiques, il manque aussi la "Gravitation quantique à boucles" ... Guérin Nicolas ( ✉ - © ) 23 avril 2007 à 19:03 (CEST)

Déplacé par LyricV 24 avril 2007 à 07:01 (CEST) depuis la contestation de l'évaluation de l'article.

Approche intuitive

"En termes plus précis, plus complets et surtout plus scientifiques que cette introduction intuitive"

Je n'aime pas trop ce passage parce que la mécanique newtonienne aussi dispose de modélisations mathématiques plus poussées. D'accord, ce sont de simples vecteurs, alors que la RG emploie des tenseurs, mais quand même!

Faudra que je glisse la remarque d'Étienne Klein sur la réfutation intuitive d'Aristote. Ça montrera que le paragraphe n'est pas un TI. Barraki Retiens ton souffle! 26 août 2007 à 00:59 (CEST)

Ce n'est pas le problème de mépriser l'approche de Newton, mais de ne parler que du problème de la chute simultanée des corps auquel il n'a rien apporté, par rapport à Gallilée, qu'une confirmation et une utilisation (avec reformulation dans le cadre de sa loi, évoquée plus bas). Einstein, avec la RG, a apporté une pensée nouvelle sur ce sujet, nottament en concluant que seul le paramètre "énergie" du corps rentre en ligne de compte dans la gravité (outre la géométrie du corps et les propriétés intrinsèques de l'espace). J'ai voulu tout évacuer d'inutile pour la compréhension de ce problème par le commun des mortels. LyricV 26 août 2007 à 13:43 (CEST)

Résumé introductif

Puisque je crois que cette article méritait un résumer introductif plus développé qu'une simple phrase: "La gravitation est une des quatre force élémentaire de la physique", je me suis permit de le reformuler. N'hésitez pas d'y apporter des corrections si vous voyez des erreurs dans mon approche possiblement simpliste du phénomène. --Le Père Odin 3 novembre 2007 à 18:16 (CET)

Compréhension intuitive: Intro

Dans la phrase suivante:

Penser, comme Aristote, que sur Terre (et avec l'hypothèse du vide atmosphérique) plus un corps est lourd, plus il tombe vite est faire une confusion entre quantité et qualité.

Est-il vraiment nécessaire de mentionner la terre, le vide atmosphérique et Aristote dans la mème phrase? Je trouve personnellement que ça l'alourdit. On s'occupe déjà de l'effet du frottement de l'air un peu plus loins, est-il vraiment besoin de le mentionner ici?

Penser que d'une façon générale, plus un corps est lourd, plus il tombe vite est faire une confusion entre quantité et qualité :

Qu'en pensez-vous? --Le Père Odin 5 novembre 2007 à 06:47 (CET)

J'avais mis cette première partie Compréhension intuitive pour expliquer, aussi simplement que je le pouvais, pourquoi la vitesse de chute est indépendante du poids de l'objet, ce qui est admis mais pas compris par tous.

Pour le vide : si on veut éviter d'être dans l'erreur, il faut en parler car dans l'air, ce qui est plus lourd tombe vraiment plus vite (à surface égale).

Pour Aristote : l'idée venait de lui, entre autres, il n'est cité que pour faire un rappel historique car Galilée a rudement bataillé contre ses idées et ses défenseurs au début du XVIIème siècle.

Pour la terre : c'était pour rappeler que l'on parle bien que de gravitation et pour faire concret aux yeux du lecteur pour qui ce problème n'est pas réglé.

Je proposerais d'enlever Aristote (mais c'est dommage, un peu d'histoire ça fait pas de mal), et le mot atmosphérique (pas utile, c'est vrai), ainsi que...la phrase que tu as mis avant qui n'apporte aucune information. Ça donne: Penser, (comme Aristote (?)) que sur Terre (mais dans le vide) « plus un corps est lourd, plus il tombe vite » est faire une confusion entre quantité et qualité.

Cordialement.LyricV 5 novembre 2007 à 10:13 (CET)

Remarque que je ne suis pas, du tout, contre l'idée de parler d'Aristote (un peu d'histoire c'est effectivement bien et je suis parfaitement d'accord à ce qu'on doit parler de la friction de l'air puisque c'est un facteur qui influence la vitesse de chute... Tu as parfaitement raison de vouloir expliquer la différence entre poids et vitesse de chute, je connais plusieurs personnes qui les confondent. Seulement, je trouvais, que de tout balancer ça dans la même phrase alourdissait la formulation de l'intro. Faudrait peut-être l'"aérer".

Ma phrase n'apporte effectivement pas grand chose (hors mi un lien vers l'article pesanteur) on peu l'enlever.--Le Père Odin 5 novembre 2007 à 14:58 (CET)

Ce lien peut s'ajouter un peu plus loin (ou avant). À chacun sa perception des choses : je préfère des phrases compactes car il me semble que quand c'est trop long le lecteur décroche, et si c'est un peu rude mais court, le lecteur peut y revenir. Mais trouver le juste équilibre entre synthèse et explications est impossible de toute façon : à chaque lecteur son appréciation. Aère autant que tu veux : dans le pire des cas, on trouvera un compromis. LyricV 5 novembre 2007 à 19:37 (CET)

juste quelques petites remarques futuristes, si je puis me permettre :

• il est probable que la gravitation soit un phénomène comparable à la lumière, un graviton et une onde; sa vitesse de propagation doit être bien supérieur à la lumière, car sinon la mécanique céleste serait vite complètement déréglée, 300 000 km/s à l'échelle de l'univers c'est la vitesse d'un char à boeufs. Hors l'univers semble cohérent.
• cette force témoigne peut être d'un lien originel, dans la boule de matière pré big bang, qui se distend comme un élastique aux confins de l'univers
• le "vide" est probablement rempli de forces, d'énergies et de particules comme le graviton, qui doivent opposer un frein au déplacement des masses, c'est ce qui doit expliquer le "ralentissement" inexpliqué d'un schutle (nom ?) envoyé dans l'espace
• la déformation de l'espace temps est une belle métaphore, mais cela doit être un problème de gravitation classique qui s'exerce sur la masse "non détectée" des photons, courbure près du soleil par exemple, le photon est bien courbé par un simple miroir
• si la vitesse de 300 000 km/s était une vitesse limite, cela induirait que le photon n'est pas sécable et ne tourne pas, car là on passerait tout de suite au double de vitesse, peu probable, ce serait bien la première brique originelle trouvée !
• le magnétisme serait plus façile à étudier en labo et à peut être des capacités de vitesse comparables
• bien sûr tout cela dépend des travaux en cours sur le mystère de la gravitation

Marc Patay

Ether et gravitation ?

Tiens, je ne savais pas que l'éther avait été introduit en premier lieu pour expliquer la propagation de la gravitation. Etant donné que l'article sur l'éther n'en parle pas, je pense qu'une source est nécessaire sur ce point. Quels physiciens, quelles théories, ont parlé d'éther en ce qui concerne la gravitation ? Cordialement --Jean-Christophe BENOIST (d) 17 juin 2008 à 09:59 (CEST)

J'ai trouvé cela dans l'article Champ du Dictionnaire d'histoire et..., on en retrouve des déclinaisons dans des textes de F Balibar, entre autres qu'il y a deux origines à l'éther : électro et gravita. Je vais lire de près ces textes. J'ai changé un mot qui pourrait faire croire que la gravitation est l'unique origine de cette idée. LyricV (d) 17 juin 2008 à 10:27 (CEST)

C'est intéressant et cela mérite d'être développé, peut-être plus dans l'article Ether où on en parle pas. --Jean-Christophe BENOIST (d) 17 juin 2008 à 11:19 (CEST)

A la réflexion, je pense que le point est que le mot "Ether" est un peu un terme fourre-tout qui veut dire "une substance dont on ne connait pas la nature et qui remplit tout l'espace". Cela peut recouvrir des idées très différentes à des époques différentes; à la limite, les "tourbillons de Descartes" pourraient être vus aussi comme un éther (mais Descartes a-t-il nommé la substance qui remplit l'espace "éther" ?). En fait tout dépend si on s'attache au mot ou à l'idée de substance; je n'ai pas l'impression que le mot "éther" ait été employé avant Huygens et dans un contexte de gravitation, mais l'idée de substance emplissant l'espace date d'avant et a été effectivement en lien avec la gravitation. Mais bon, tout ce débat concerne plutôt l'article "ether". Pour que tout soit clair, il faudrait que cet article parle de la notion de substance en lien avec la gravitation, et même pour des idées n'ayant pas été nommées "ether". --Jean-Christophe BENOIST (d) 17 juin 2008 à 11:37 (CEST)

L'article éther du Dictionnaire d'histoire et philo... commence par parler des tourbillons de Descartes. Et Newton ne semble pas utiliser le mot éther, c'est Einstein, et F Balibar à sa suite, qui semble l'utiliser dans le cadre gravitationnel pour désigner l'esprit très subtil de Newton. Les textes de F Balibar que j'ai ne donnent pas d'autre nom de physicien l'utilisant dans le même sens. LyricV (d) 17 juin 2008 à 12:45 (CEST)

Vu. Convaincu. Reste à parler de tout cela dans l'article Ether.. --Jean-Christophe BENOIST (d) 17 juin 2008 à 12:55 (CEST)

A illustrer

Animer les modélisation de Newton et Einstein. — Le message qui précède, non signé, a été déposé par Azariel (discuter) le 6 février 2009 à 17:43.

Bonjour Azariel. je sais que vous voulez lancer un projet animation, ce qui est à mon sens une bonne chose. Cependant, il n'est pas indispensable de mettre systématiquement des images animées sur des articles de nature scientifique comme celui-ci qui est déjà bien illustré. Toutefois, vous avez la possibilité de placer, si vous le souhaitez dans une section appropriée de l'article cette animation par exemple. GLec (d) 6 février 2009 à 18:47 (CET)

Explications

Je lis le paragraphe sur la modélisation d'Albert Einstein et la première question qui me vient,c'est "comment la matière modifie l'espace temps,si ce n'est avec...son poids ?".Si quelqu'un pouvait ajouter une explication,ce serait pas mal,je n'est pas les connaissances pour expliquer ça.Kl4wY,23/06/10

Avec son poids ? Non, avec sa masse ou plutôt son énergie : voir relativité générale ou introduction à la relativité générale. Cordialement.--LyricV (d) 23 juin 2010 à 23:39 (CEST)

J'ai...

Suite à ce que j'avais suggéré, l'actuelle version de cet article est acceptable : je ne vais donc pas continuer la polémique. Cependant, vu la remarque " quelle référence ?" concernant mon affirmation pour le comportement identique, face à la gravitation, de deux atomes de deutérium et d'un atome d'hélium-4, je vais poursuivre mes recherches. GMC

J'ai rajouté un paragraphe didactique dans une forme plus explicite que celui déjà introduit en 2003. Je continue de penser qu'introduire une intrigue posée par l'interprétation mécanique de la gravitation sans expliquer quelle est concrètement cette intrigue n'éclaire pas vraiment le lecteur. Einstein lui-même l'a imagé. J'ai fait le test auprès de béotiens, ce paragraphe introduit bien, il me semble, le problème posé. Sans celui-ci, on débouche de manière très abrupte sur le principe d'équivalence. David Pierre

A mon avis sans les altérer, j'ai légèrement complété certains paragraphes car les connaissances progressent de jour en jour. GLOBALEMENT : Excellent article. Supprimer les modifications du 25/11/2010 conduit à manquer d'objectivité et à ignorer plusieurs faits importants guy.cholet@db mail.com (membre SAF et Commission Cosmologie) le 26 novembre 2010 à 12:35

Modifications pertinentes. Merci ! --Jean-Christophe BENOIST (d) 25 novembre 2010 à 16:05 (CET)

O. K. pour la remarque faite par LyricV (d) 27 novembre 2010 à 07:30 (CET) Si cela est l'habitude, je la respecterais et écrirai en bas de page  ; j'avais seulement estimé que, en particulier quand il y avait une longue suite de remarques, il était fréférable de les regrouper par thème. GMC

Incohérence

Pourquoi commencer l'article par "La gravitation, l'une des quatre forces fondamentales" puisqu'on explique ensuite qu'au sens d'Einstein la gravitation n'est pas une force. — Le message qui précède, non signé, a été déposé par un utilisateur sous l’IP 157.99.221.35 (discuter), le 25 juillet 2017 à 11:50‎.

Elle n'est pas une force si on voit l'univers à 4 dimensions, l'espace-temps. Elle est une force si on considère l'espace et le temps séparément (sens classique, et même en physique quantique). "Force", par défaut, est à prendre dans son sens classique. --Jean-Christophe BENOIST (discuter) 25 juillet 2017 à 13:22 (CEST)