نقاط هم‌دایره

در هندسه، به مجموعه‌ای از نقاط که بر روی یک دایره یاشند، هم‌دایره (concyclic) گویند.

همرسی عمود منصف وترهای بین نقاط هم‌دایره.

چهار نقطهٔ هم‌دایره که یک چهار ضلعی محاطی را تشکیل داده‌اند، دو زاویهء مساوی نمایش داده شده‌اند.

عمود منصف

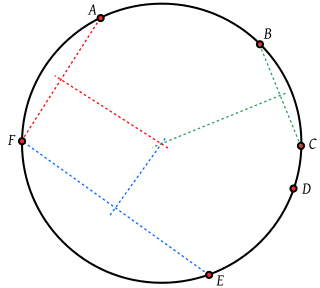
عمود منصف پاره خط بین دو نقطه روی یک دایره از مرکز دایره می‌گذرد.^[1]برای n نقطه روی یک دایره اگر به صورت متوالی نقاط را به هم وصل کنیم n(n − ۱)/۲ پاره خط و بالتبع همین تعداد عمود منصف گذرنده از مرکز دایره داریم.

چند ضلعی محاطی

همهٔ مثلث‌ها محاطی اند، به همین علت از این لحاظ دسته‌بندی نمی‌شوند.^[2] به دایره‌ای که رئوس مثلث بر آن واقع اس، محیطی گویند و رابطهٔ شعاع آن با اضلاع مثلث به صورت زیر است:

${\displaystyle R={\sqrt {\frac {a^{2}b^{2}c^{2}}{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}.}$

وقتی رئوس چهار ضلعی'ABCD' هم‌دایره باشند، به این چهارضلعی محاطی گویند. این شرایط زمانی وقتی رخ می‌دهد که ${\displaystyle \angle CAD=\angle CBD}$ (قضیه زاویه محاطی) و زاویه‌های متقابل مکمل باشند.^[3] همچنین اگر s= (a+b+c+d)/2 نمایندهٔ نصف محیط چهار ضلعی باشد خواهیم داشت:^[4][5]

${\displaystyle R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}},}$

که پارامشوارا ریاضی‌دان هندی در قرن ۱۵ آن را بدست آورد.

همچنین بر اساس قضیه بطلمیدوس اگر قطرهای چهارضلعی را داشته باشیم، چهارضلعی محاطی است، اگر و تنها اگر:

${\displaystyle AC\cdot BD=AB\cdot CD+BC\cdot AD.}$

همچنین اگر قطرها یکدیگر را در نقطهٔ X قطع کنند. چهارضلعی محیطی است، اگر و تنها اگر^[6]

${\displaystyle \displaystyle AX\cdot XC=BX\cdot XD.}$

همچنین یک چهارضلعی محاطی است، اگر و تنها اگر عمود منصف اضلاع همرس باشند.^[7]

وردش

برخی بر این باورند که نقاط هم راستا هم هم‌دایره اند بر روی دایره‌ای با شعاع بی‌نهایت.

دیگر خصوصیات

یک چند ضلعی محاطی است، اگر و تنها اگر هر ۴ راس آن یک چهارضلعی محاطی باشد.^[8]

منابع

1. Libeskind, Shlomo (2008), Euclidean and Transformational Geometry: A Deductive Inquiry, Jones & Bartlett Learning, p. 21, ISBN 9780763743666/
2. Elliott, John (1902), Elementary Geometry, Swan Sonnenschein & co., p. 126.
3. Pedoe, Dan (1997), Circles: A Mathematical View, MAA Spectrum (2nd ed.), Cambridge University Press, p. xxii, ISBN 9780883855188.
4. Alsina, Claudi; Nelsen, Roger B. (2007), "On the diagonals of a cyclic quadrilateral" (PDF), Forum Geometricorum, 7: 147–9
5. Hoehn, Larry (March 2000), "Circumradius of a cyclic quadrilateral", Mathematical Gazette, 84 (499): 69–70, JSTOR 3621477
6. Bradley, Christopher J. (2007), The Algebra of Geometry: Cartesian, Areal and Projective Co-Ordinates, Highperception, p. 179, ISBN 1906338000, OCLC 213434422
7. Byer, Owen; Lazebnik, Felix; Smeltzer, Deirdre L. (2010), Methods for Euclidean Geometry, Mathematical Association of America, p. 77, ISBN 9780883857632.
8. Pedoe, Dan (1988), Geometry: A Comprehensive Course, Courier Dover Publications, p. 431, ISBN 9780486658124.