ضرب خارجی

در ریاضیات، ضرب خارجی (به انگلیسی: Cross Product)، یا ضرب برداری (به انگلیسی: Vector Product)، یک عمل دوتایی (با نماد ×^[۱]) بین دو بردار اقلیدسی در فضای سه‌بعدی است که نتیجهٔ آن برداری است که بر هر دو بردار اولیه عمود است.

تعریف

بیان ریاضی

برای بردار‌های یکّهٔ پایه تساوی‌های زیر برقرار اند^[۲][۳]:

روشی برای حفظ کردن ضرب خارجی ${\displaystyle {\hat {i}}}$ و ${\displaystyle {\hat {j}}}$ و ${\displaystyle {\hat {k}}}$

${\displaystyle {\hat {i}}\times {\hat {j}}=-{\hat {j}}\times {\hat {i}}={\hat {k}}}$

${\displaystyle {\hat {j}}\times {\hat {k}}=-{\hat {k}}\times {\hat {j}}={\hat {i}}}$

${\displaystyle {\hat {k}}\times {\hat {i}}=-{\hat {i}}\times {\hat {k}}={\hat {j}}}$

${\displaystyle {\hat {i}}\times {\hat {i}}={\vec {0}}\qquad {\hat {j}}\times {\hat {j}}={\vec {0}}\qquad {\hat {k}}\times {\hat {k}}={\vec {0}}}$

از تساوی‌های فوق می‌توان فرمول ضرب خارجی را نتیجه گرفت^[۲]:

اگر ${\displaystyle {\vec {a}}=(a_{x},a_{y},a_{z})}$ و ${\displaystyle {\vec {b}}=(b_{x},b_{y},b_{z})}$:

${\displaystyle {\vec {a}}\times {\vec {b}}=(a_{y}b_{z}-a_{z}b_{y},a_{z}b_{x}-a_{x}b_{z},a_{x}b_{y}-a_{y}b_{x})}$

بیان ماتریسی

برای حفظ‌کردن راحت‌تر ضرب خارجی می‌توان از تساوی زیر کمک گرفت^[۲][۳]:

${\displaystyle {\vec {a}}\times {\vec {b}}={\begin{vmatrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\\\end{vmatrix}}}$

این دترمینان را می‌توان با روش ساروس محاسبه کرد که در نهایت به فرمول بیان ریاضی می‌رسد.

بیان هندسی

قانون دست راست

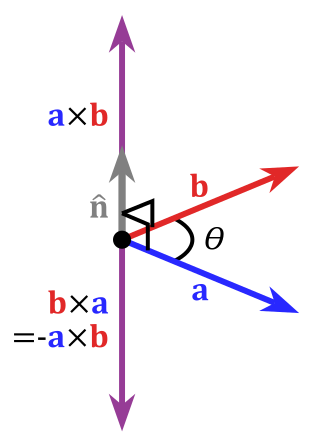
جهت بردارِ حاصل از ضرب خارجی، عمود بر هر دو بردار ${\displaystyle {\vec {a}}}$ و ${\displaystyle {\vec {b}}}$ است و به کمک قانون دست راست قابل تشخیص است و طول آن برابر مساحت متوازی‌الاضلاعی با اضلاع بردار‌های اوّلیّه است^[۴]؛ پس اگر ${\displaystyle \theta }$ زاویهٔ بین دو بردار باشد^[۲]:

${\displaystyle \left\vert {\vec {a}}\times {\vec {b}}\right\vert =\left\vert {\vec {a}}\right\vert \left\vert {\vec {b}}\right\vert \sin \theta }$

اگر بردار‌ها هم‌راستا باشند یا یکی از بردار‌ها صفر باشد، حاصل ضرب خارجی صفر خواهد شد.

خواص

• 

  جابه‌جایی ندارد ولی^[۲]: ${\displaystyle {\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}}$
• پخش‌پذیری^[۲]: ${\displaystyle {\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}}$
• شرکت‌پذیری ندارد ولی از تساوی جاکوبی پیروی می‌کند: ${\displaystyle {\vec {a}}\times ({\vec {b}}\times {\vec {c}})+{\vec {b}}\times ({\vec {c}}\times {\vec {a}})+{\vec {c}}\times ({\vec {a}}\times {\vec {b}})={\vec {0}}}$
• ضرب در عدد^[۲]: ${\displaystyle (r{\vec {a}})\times {\vec {b}}={\vec {a}}\times (r{\vec {b}})=r({\vec {a}}\times {\vec {b}})}$
• ${\displaystyle {\vec {a}}\times {\vec {a}}={\vec {0}}}$
• ${\displaystyle {\vec {a}}\times {\vec {b}}={\vec {0}}\Longleftrightarrow {\vec {a}}\parallel {\vec {b}}}$^[۲]

اتّحاد لاگرانژ

به کمک اتّحاد لاگرانژ می‌توان دریافت^[۵]:

${\displaystyle \left\vert {\vec {a}}\times {\vec {b}}\right\vert ^{2}=\left\vert {\vec {a}}\right\vert ^{2}\left\vert {\vec {b}}\right\vert ^{2}-({\vec {a}}\cdot {\vec {b}})^{2}}$