ساخت با خطکش و پرگار (به انگلیسی: Straightedge and Compass Construction) (یا Ruler-and-Compass Construction) (یا ترسیم با خطکش و پرگار یا ساخت کلاسیک)، به ساخت طول‌ها، زوایا، و سایر اشکال هندسی با استفاده از خطکش و پرگار ایده‌آل گفته می شود.
خطکش و پرگار تنها ابزارهای مجاز ترسیم در هندسه اقلیدسی هستند،[1] تا جایی که هندسهٔ اقلیدسی گاه «هندسهٔ خطکش و پرگار» خوانده شده‌است.[2] پرگار ابزاری برای کشیدن دایره بر اساس تعریف اقلیدسی آن است[3] و با خط‌کشی با طول بی‌نهایت می‌توان خط راست کشید، و هدف ریاضی‌دانان اقلیدسی این بود که همهٔ اشکال را با این دو ابزار بسازند.[4] بنابراین در ترسیم با خطکش و پرگار تنها از سه اصل اول اصول موضوعه هندسه اقلیدسی می‌توان استفاده کرد. بنابر اثبات گاوس، تنها شکل‌هایی را می‌توان با خطکش و پرگار رسم کرد که اندازه‌شان عدد ترسیم‌پذیر باشد. اعداد ترسیم‌پذیر اعدادی‌اند که بتوان آن‌ها را با اعمال چهار عمل اصلی و ریشه دوم بر یک عدد ترسیم‌پذیر دیگر به دست آورد (صفر و یک بنابر تعریف ترسیم‌پذیرند).
ترسیم‌های بنیادی
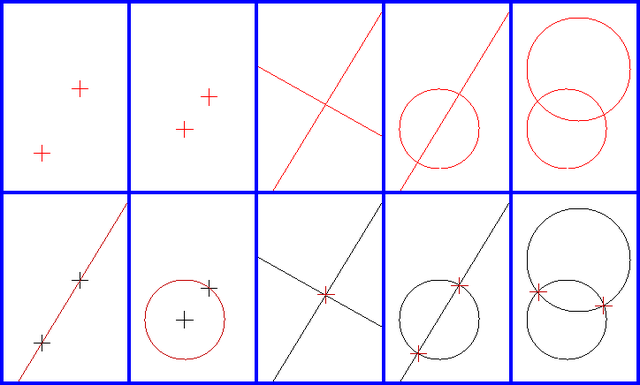
همهٔ ترسیم‌ها با خطکش و پرگار با تکرار و ترکیب پنج ترسیم بنیادی در صفحه صورت می‌گیرند. این پنج ترسیم بنیادی عبارتند از:
- ساخت یک خط با داشتن دو نقطه (اصل اول از اصول موضوعه هندسه اقلیدسی)
- ساخت یک دایره با داشتن دو نقطه (اصل سوم از اصول موضوعه هندسه اقلیدسی)
- ساخت یک نقطه در محل تقاطع دو خط ناموازی
- ساخت دو نقطه در محل تقاطع یک خط و یک دایره (در صورت تقاطع)
- ساخت دو نقطه در محل تقاطع دو دایره (در صورت تقاطع)
برخی ترسیم‌های خطکش و پرگار
 |
تنصیف زاویه: برای رسم نیمساز زاویه ابتدا به مرکزیت رأس زاویه () کمانی به شعاع دلخواه زده شود و نقاط تقاطع آن با اضلاع زاویه ( و ) مشخص شود. سپس به مرکزیت و دو کمان با شعاع مساوی و بزرگتر از نصف زده شود. با اتصال نقاط تقاطع این کمان، نیمساز زاویه حاصل می‌شود.[5] |
 |
ترسیم عمودمنصف پاره‌خط: به شعاع بیش از نصف طول پاره‌خط دو کمان به مرکزیت دو سر پاره‌خط زده می‌شود. با وصل کردن نقاط تقاطع دو کمان، عمودمنصف پاره‌خط حاصل می‌شود.[6] |
 |
رسم عمودی بر خط از نقطه‌ای بیرون آن: به مرکزیت نقطه کمانی به شعاع دلخواه زده می‌شود تا خط را در و قطع کند. سپس به روش مذکور در بالا عمودمنصف پاره خط ترسیم می‌شود.[7] |
 |
ترسیم دایره با داشتن سه نقطه غیرهم‌خط ، ، و : به روش بالا عمودمنصف پاره‌خط‌های و رسم می‌شود. نقطهٔ تقاطع دو عمودمنصف مرکز دایره است و می‌توان از آن به فاصلهٔ هر کدام از نقاط دایره را رسم کرد. |
ترسیم‌های غیرممکن
تربیع دایره
تربیع دایره از مسائل کهن ریاضی است و هدف آن ترسیم مربعی با خطکش و پرگار است که مساحت آن با مساحت دایره‌ای مفروض برابر باشد. شکل دیگری از مسئله ترسیم مربعی با خطکش و پرگار است که محیط آن با محیط دایرهٔ مفروض برابر باشد.[8] در ۱۸۸۲ فردیناند فون لیندمن نشان داد که پی عددی متعالی است، و تربیع دایره غیرممکن است. در زبان انگلیسی «تربیع دایره» (به انگلیسی: squaring the circle) وارد ادبیات شده‌است و همچنین ضرب‌المثلی به مفهوم «عمل غیرممکن» است.[9]
تضعیف مکعب
تضعیف مکعب یا «مسئلهٔ دلوسی» نیز یکی مسائل کهن ریاضی است و هدفش ترسیم مکعبی با خطکش و پرگار است که حجم آن دو برابر حجم مکعبی مفروض باشد؛ به عبارت دیگر هر ضلع مکعب مطلوب باید برابر ضلع مکعب مفروض باشد.[10] پیر ونزل در ۱۸۳۷ نشان داد که این مسئله جوابی ندارد.
![{\displaystyle {\sqrt[{3}]{2}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
تثلیث زاویه
تثلیث زاویه سومین مسئلهٔ بزرگ کهن ریاضی است و هدف آن تقسیم زاویه به سه قسمت مساوی با خطکش و پرگار است.[11] پیر ونزل در ۱۸۳۷ نشان داد که این مسئله جوابی ندارد.
جستار های وابسته
منابع
پیوند به بیرون
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
