EU
All
Articles
Dictionary
Quotes
Map

Wikiwand ❤️ Wikipedia

PrivacyTerms
Koordenatu esferiko

Koordenatu esferiko

Hiru dimentsioko espazioan puntu bat finkatzeko erabiltzen diren koordenatu hauetako bakoitza: polo izeneko jatorri-puntu baterainoko distantzia (ρ), OXY planoko angelu azimutala (θ) OX ardatzetik, 0 ≤ θ < 2Π izanik, eta angelu polarra (φ) OZ arda. From Wikipedia, the free encyclopedia

Koordenatu esferiko
Erabilitako hitzarmenakNazioarteko hitzarmenaAEBetako hitzarmenaBeste koordenatu-sistema batzuekiko erlazioaKoordenatu kartesiarrekiko erlazioaKoordenatu zilindrikoekiko erlazioaKanpo estekak

Koordenatu esferikoen sistema koordenatu polarren ideia berean oinarritzen da eta puntu baten posizio espaziala distantzia eta bi angelu erabiliz zehazteko erabiltzen da. Ondorioz, P puntu bat hiru magnitudeen multzo baten bidez adierazten da: r {\displaystyle r} {\displaystyle r} erradioa, θ {\displaystyle \theta } {\displaystyle \theta } angelu polarra edo kolatitudea eta φ {\displaystyle \varphi } {\displaystyle \varphi } azimutula.

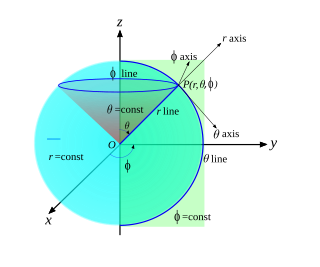
Thumb
Koordenatu esferikoen elementuak

Autore batzuek kolatitudearen ordez latitudea erabiltzen dute, eta kasu horretan bere marjina -90°-tik 90°-ra bitartekoa da (-π/2-tik π/2-ra radian), zeroa XY planoa izanik. Azimutalaren neurria ere alda daiteke, angelua erlojuaren orratzen noranzkoan edo erlojuaren aurkako noranzkoan neurtzen den arabera, eta 0°-tik 360°-ra (0-tik 2π-ra radianetan) edo -180°-tik +180°-ra (-π-tik π-ra).

Egile batek zein konbentzio erabiltzen duen jakin beharko zenuke.

Nazioarteko hitzarmena

Thumb

Estatubatuar ez diren fisikari, ingeniari eta matematikari gehienek idazten dute:

  • φ {\displaystyle \varphi } {\displaystyle \varphi }, azimutala : 0°-tik 360°-ra
  • θ {\displaystyle \theta } {\displaystyle \theta }, kolatitudea : 0°-tik 180°-ra

Hau da artikulu honetan jarraitzen dugun konbentzioa. Nazioarteko sisteman, hiru koordenatuen aldakuntza-eremuak hauek dira:

0 ≤ r < ∞ 0 ≤ θ ≤ π 0 ≤ φ < 2 π {\displaystyle 0\leq r<\infty \qquad 0\leq \theta \leq \pi \qquad 0\leq \varphi <2\pi } {\displaystyle 0\leq r<\infty \qquad 0\leq \theta \leq \pi \qquad 0\leq \varphi <2\pi }

Koordenatu erradiala beti da positiboa. r {\displaystyle r} {\displaystyle r}-ren balioa murriztuz 0 baliora iristen bada, hortik aurrera, r {\displaystyle r} {\displaystyle r}; berriro handitzen da, baina θ {\displaystyle \theta } {\displaystyle \theta } balio du π- θ {\displaystyle \theta } {\displaystyle \theta } eta φ {\displaystyle \varphi } {\displaystyle \varphi } π radianetan handitzen edo gutxitzen da.

AEBetako hitzarmena

Gaur egun, AEBetan erabiltzen den konbentzioa ez da europarraren bera. Angelu azimutala adierazteko θ {\displaystyle \theta } {\displaystyle \theta } erabiltzen da, eta polarra, latitudea edo kolatitudea adierazteko φ {\displaystyle \varphi } {\displaystyle \varphi } erabiltzen da.

Koordenatu kartesiarrekiko erlazioa

Multzo irekiei buruz:

U = { ( r , θ , φ ) | r > 0 , 0 < θ < π , 0 ≤ φ < 2 π } eta V = { ( x , y , z ) | x 2 + y 2 + z 2 > 0 } {\displaystyle U=\{(r,\theta ,\varphi )|r>0,0<\theta <\pi ,0\leq \varphi <2\pi \}\qquad {\mbox{eta}}\qquad V=\{(x,y,z)|x^{2}+y^{2}+z^{2}>0\}} {\displaystyle U=\{(r,\theta ,\varphi )|r>0,0<\theta <\pi ,0\leq \varphi <2\pi \}\qquad {\mbox{eta}}\qquad V=\{(x,y,z)|x^{2}+y^{2}+z^{2}>0\}}

Koordenatu kartesiar eta esferikoen arteko F : V → U {\displaystyle F:V\to U} {\displaystyle F:V\to U} korrespondentzia unibokoa dago erlazio hauek definitutakoak:

r = x 2 + y 2 + z 2 θ = { arctan ⁡ ( x 2 + y 2 z ) z > 0 π 2 z = 0 π + arctan ⁡ ( x 2 + y 2 z ) z < 0 φ = { arctan ⁡ ( y x ) x > 0  y  y > 0  (1° Q) 2 π + arctan ⁡ ( y x ) x > 0  y  y < 0  (4° Q) π 2 sgn ( y ) x = 0 π + arctan ⁡ ( y x ) x < 0  (2° y 3° Q) {\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}\qquad \theta ={\begin{cases}\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)&z>0\\{\frac {\pi }{2}}&z=0\\\pi +\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)&z<0\end{cases}}\qquad \varphi ={\begin{cases}\arctan \left({\frac {y}{x}}\right)&x>0{\mbox{ y }}y>0{\mbox{ (1° Q)}}\\2\pi +\arctan \left({\frac {y}{x}}\right)&x>0{\mbox{ y }}y<0{\mbox{ (4° Q)}}\\{\frac {\pi }{2}}{\mbox{sgn}}(y)&x=0\\\pi +\arctan \left({\frac {y}{x}}\right)&x<0{\mbox{ (2° y 3° Q)}}\end{cases}}} {\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}\qquad \theta ={\begin{cases}\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)&z>0\\{\frac {\pi }{2}}&z=0\\\pi +\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)&z<0\end{cases}}\qquad \varphi ={\begin{cases}\arctan \left({\frac {y}{x}}\right)&x>0{\mbox{ y }}y>0{\mbox{ (1° Q)}}\\2\pi +\arctan \left({\frac {y}{x}}\right)&x>0{\mbox{ y }}y<0{\mbox{ (4° Q)}}\\{\frac {\pi }{2}}{\mbox{sgn}}(y)&x=0\\\pi +\arctan \left({\frac {y}{x}}\right)&x<0{\mbox{ (2° y 3° Q)}}\end{cases}}}

Erlazio horiek bereziak egiten dira z {\displaystyle z\,} {\displaystyle z\,}ardatz berera hedatzen saiatzen direnean, non x 2 + y 2 = 0 {\displaystyle x^{2}+y^{2}=0} {\displaystyle x^{2}+y^{2}=0}, zeinetan φ, ez dagoen definituta. Gainera, φ ez da inongo ( x ,   y ,   z ) {\displaystyle (x,\ y,\ z)} {\displaystyle (x,\ y,\ z)} puntutan jarraitua x = 0 {\displaystyle x=0\;} {\displaystyle x=0\;} bada.

Alderantzizko funtzioa F − 1 {\displaystyle F^{-1}} {\displaystyle F^{-1}} ireki berdinen arteko alderantzizko erlazioen arabera idatz daiteke:

x = r sin θ cos ⁡ φ y = r sin θ sin φ z = r cos ⁡ θ {\displaystyle x=r\sin \,\theta \,\cos \varphi \qquad y=r\sin \,\theta \sin \,\varphi \qquad z=r\,\cos \theta } {\displaystyle x=r\sin \,\theta \,\cos \varphi \qquad y=r\sin \,\theta \sin \,\varphi \qquad z=r\,\cos \theta }

Bere jacobtarra izanik: | J | = r 2 sin ⁡ θ {\displaystyle \left\vert J\right\vert =r^{2}\sin \theta } {\displaystyle \left\vert J\right\vert =r^{2}\sin \theta }

Thumb
Koordenatu esferikoak eta erlazionatutako ardatz kartesiarrak

Koordenatu zilindrikoekiko erlazioa

Koordenatu kartesiar eta esferikoen arteko tarteko sistema gisa, koordenatu zilindrikoena dago, erlazio hauen bidez koordenatu esferikoekin erlazionatuta dagoena:

r = ρ 2 + z 2 θ = arctan ⁡ ( ρ z ) φ = φ {\displaystyle r={\sqrt {\rho ^{2}+z^{2}}}\qquad \theta =\arctan \left({\frac {\rho }{z}}\right)\qquad \varphi =\varphi } {\displaystyle r={\sqrt {\rho ^{2}+z^{2}}}\qquad \theta =\arctan \left({\frac {\rho }{z}}\right)\qquad \varphi =\varphi }

eta haien alderantzizkoak

ρ = r sin θ φ = φ z = r cos ⁡ θ {\displaystyle \rho =r\,{\sin }\,\theta \qquad \varphi =\varphi \qquad z=r\,\cos \theta } {\displaystyle \rho =r\,{\sin }\,\theta \qquad \varphi =\varphi \qquad z=r\,\cos \theta }
  • Wd Datuak: Q203218
  • Commonscat Multimedia: Spherical coordinates / Q203218
Edit in WikipediaRevision historyRead in Wikipedia

Wikiwand in your browser!

Seamless Wikipedia browsing. On steroids.

Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.

Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.

Chrome
Wikiwand for Chrome
Edge
Wikiwand for Edge
Firefox
Wikiwand for Firefox

Erabilitako hitzarmenak

Beste koordenatu-sistema batzuekiko erlazioa

Kanpo estekak