Masa gravitatoria

La masa gravitatoria es la medida de la fuerza de atracción gravitatoria que experimenta una porción de materia básica dentro de un campo gravitatorio.

Aunque numéricamente idéntica a la masa inercial, conceptualmente difiere de esta. En el seno de la mecánica clásica resultó por mucho tiempo un misterio el por qué la masa gravitatoria era numéricamente igual a la masa inercial, de ahí que usualmente se hable simplemente de masa (sin especificar si se trata de la inercial o la gravitatoria), al ser ambas numéricamente idénticas.

La teoría de la relatividad general, al explicar el campo gravitatorio como un efecto de la curvatura del espacio-tiempo, aclaró que de hecho la masa gravitatoria tiene que coincidir numéricamente con la masa inercial.

Masa gravitatoria en la teoría newtoniana

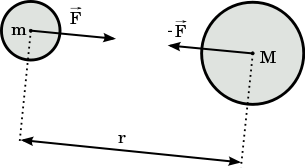
La fuerza gravitatoria entre dos partículas viene dada por:

${\displaystyle F_{G}=G{\frac {m_{g}M_{g}}{r^{2}}}}$

Donde

${\displaystyle G\,}$ es la constante de gravitación universal cuyo valor es ${\displaystyle (6{,}67428\pm 0{,}00067)\cdot 10^{-11}~\mathrm {\frac {m^{3}}{kg\cdot s^{2}}} }$

${\displaystyle m_{g}\,}$ y ${\displaystyle M_{g}\,}$ son las masas gravitatorias de las partículas y

${\displaystyle r\,}$ es la distancia entre ellas.

Por otra parte, las masas inerciales de ambas partículas vienen dadas por la razón entre esta fuerza y la aceleración experimentada por las mismas:

${\displaystyle m_{i}={\frac {F_{G}}{a_{i}}},\qquad M_{i}={\frac {F_{G}}{A_{i}}}}$

Hasta donde la precisión de los experimentos ha permitido se ha observado experimentalmente que:

${\displaystyle m_{g}=m_{i},\qquad M_{g}=M_{i}}$

Es decir, que ambos valores coinciden. En el seno de la teoría clásica no existe una explicación convincente para esperar dicha igualdad.

Masa gravitatoria activa y pasiva

Cuando se habla de campos suele distinguirse entre masas gravitatorias activa y pasiva. La activa es la que crea el campo y la pasiva la que es acelerada como consecuencia de estar en él. Esto es una buena aproximación en problemas de masas muy distintas donde una es despreciable frente a la otra, como el caso de la Tierra girando alrededor del Sol. Los experimentos de Eötvös (1885-1909) realizados por Loránd Eötvös y sus colaboradores encontraron que con una altísima precisión la masa gravitatoria pasiva y la masa inercial eran iguales, no encontrándose ninguna diferencia significativa entre ambas. La teoría de la relatividad general explicaría por primera vez que estas masas deben ser iguales: los cuerpos siguen líneas geodésicas en el espacio-tiempo curvo, por lo que en realidad la deflexión aparante de las trayectorias están causadas por esa curvatura. En el contexto de la relatividad general la masa gravitatoria pasiva y la masa inercial deben ser idénticas. Más problemático es el concepto de masa gravitatoria activa, es decir, cuanto contribuye a curvatura del espacio-tiempo una cierta cantidad de materia másica, de hecho, en general ni siquiera parece ser posible definir la masa gravitatoria de manera general (ver masa y energía en relatividad general).

Masa gravitatoria en mecánica relativista

Artículo principal: Masa y energía en relatividad general

La teoría de la relatividad general trata el campo gravitatorio desde un punto de vista relativista. Uno de las asunciones básicas de dicha teoría es que toda partícula material libre sobre la que no actúen fuerzas electromagnéticas (ignoraremos aquí las fuerzas nucleares de corto alcance) se mueve a lo largo de una línea geodésica del espacio-tiempo. Por lo que la ecuación de movimiento en términos del tiempo propio de la partícula viene dada por:

(1)${\displaystyle {\cfrac {d^{2}x^{\mu }}{d\tau ^{2}}}+\sum _{\sigma ,\nu }\Gamma _{\sigma \nu }^{\mu }{\cfrac {dx^{\sigma }}{d\tau }}{\cfrac {dx^{\nu }}{d\tau }}=0}$

Cuando sobre la partícula actúa una fuerza, entonces la ecuación del movimiento es:

(2)${\displaystyle m_{i}\left({\cfrac {d^{2}x^{\mu }}{d\tau ^{2}}}+\sum _{\sigma ,\nu }\Gamma _{\sigma \nu }^{\mu }{\cfrac {dx^{\sigma }}{d\tau }}{\cfrac {dx^{\nu }}{d\tau }}\right)=F^{\mu }}$

En un campo gravitatorio, los símbolos de Christoffel se caracterizan por no anularse idénticamente en todos los puntos del espacio, lo cual implica que éste es curvo. Si además la fuerza es nula la ecuación (2) con ${\displaystyle \scriptstyle F^{\mu }}$ se convierte en el caso particular (1). De donde se sigue que la masa gravitatoria coincide la masa inercial de la partícula, y la curvatura de la trayectoria en ese caso es un efecto de la curvatura del espacio-tiempo. Para la teoría general de la relatividad la masa gravitatoria pasiva es exactamente igual a la masa inercial. Sin embargo, el concepto de masa gravitatoria activa que es un concepto de definir, ya que para la esta teoría no es propiamente la masa, sino el contenido del tensor energía-impulso lo que da la intensidad de la curvatura del espacio-tiempo, es decir, su efecto gravitatorio.

Masa gravitatoria en mecánica cuántica

Desde junio del 2010, Endre Kajari y su equipo en la Universidad de Ulm trabajan en una teoría que separa ambas masas a niveles cuánticos.^{[1][2] [3]}

Véase también

• Masa
• Masa inercial

Referencias

1. «New Quantum Theory Separates Gravitational and Inertial Mass» (en inglés). technologyreview.com. 14 de junio de 2010. Archivado desde el original el 18 de junio de 2010. Consultado el 22 de junio de 2010.
2. arΧiv:1006.1988
3. «Nueva teoría cuántica separa las masas gravitatoria e inercial». cienciakanija.wordpress.com. Consultado el 22 de junio de 2010.

• Datos: Q1076402