Método Schulze

El método Schulze es un sistema de votación desarrollado en 1997 por Markus Schulze que selecciona a un ganador a partir de las preferencias de los votantes. El método también puede usarse para crear una lista de ganadores.

Descripción del método

El método Schulze consiste en:

1. Averiguar el conjunto de Schwartz (el menor conjunto de candidatos que no es ganado por nadie fuera del conjunto). Si solo hay un candidato en el conjunto, este es el ganador de Condorcet. Si hay varios miembros pero no hay derrotas entre ellos, entonces hay un empate normal entre ellos.
2. En cualquier otro caso, eliminar la derrota más suave en el conjunto de Schwartz (es decir, aquella ganada por el menor margen). Recalcular el nuevo conjunto de Schwartz y repetir el proceso.

Ejemplo 1

Ejemplo (45 votantes; 5 candidatos):

5 ACBED (es decir, cinco votantes eligieron el siguiente orden de preferencia: A > C > B > E > D)

5 ADECB

8 BEDAC

3 CABED

7 CAEBD

2 CBADE

7 DCEBA

8 EBADC

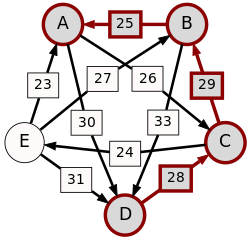
Luego, se lleva a cabo las confrontaciones entre pares (método Condorcet); por ejemplo, al comparar A y B, hay 5 + 5 + 3 + 7 = 20 votantes que prefieren A sobre B, y 8 + 2 + 7 + 8 = 25 votantes que prefieren B sobre A. Así d[A, B] = 20 y d[B, A] = 25. El conjunto completo es:

Matriz de duelos entre candidatos

	d[*,A]	d[*,B]	d[*,C]	d[*,D]	d[*,E]
d[A,*]		20	26	30	22
d[B,*]	25		16	33	18
d[C,*]	19	29		17	24
d[D,*]	15	12	28		14
d[E,*]	23	27	21	31

Para cada par de candidatos X e Y, la siguiente tabla muestra la ruta más fuerte desde el candidato X al candidato Y en red, con el más débil subrayado.

Rutas más fuertes

	... a A	... a B	... a C	... a D	... a E
de A ...		A-(30)-D-(28)-C-(29)-B	A-(30)-D-(28)-C	A-(30)-D	A-(30)-D-(28)-C-(24)-E
de B ...	B-(25)-A		B-(33)-D-(28)-C	B-(33)-D	B-(33)-D-(28)-C-(24)-E
de C ...	C-(29)-B-(25)-A	C-(29)-B		C-(29)-B-(33)-D	C-(24)-E
de D ...	D-(28)-C-(29)-B-(25)-A	D-(28)-C-(29)-B	D-(28)-C		D-(28)-C-(24)-E
de E ...	E-(31)-D-(28)-C-(29)-B-(25)-A	E-(31)-D-(28)-C-(29)-B	E-(31)-D-(28)-C	E-(31)-D

Robustez de las rutas más fuertes

	p[*,A]	p[*,B]	p[*,C]	p[*,D]	p[*,E]
p[A,*]		28	28	30	24
p[B,*]	25		28	33	24
p[C,*]	25	29		29	24
p[D,*]	25	28	28		24
p[E,*]	25	28	28	31

Con esta matriz es posible determinar el resultado por el método Schulze. Por ejemplo, al comparar A y B, ya que 28 = p [A, B]> p [B, A] = 25, el candidato A es mejor que el candidato B. Otro ejemplo es que 31 = p [E, D]> p [D, E] = 24, por lo que el candidato E es mejor que el candidato D. Si se continúa de esta manera, el resultado es que el ranking Schulze es E > A> C> B> D; en consecuencia, E gana. En otras palabras, E es un ganador potencial porque p[E,X] ≥ p[X,E] para cualquier otro candidato X.

Enlaces externos

• Proposed Statutory Rules for the Schulze Single-Winner Election Method by Markus Schulze (en inglés)
• A New Monotonic and Clone-Independent Single-Winner Election Method by Markus Schulze (mirrors: ) (en inglés)
• A New Monotonic, Clone-Independent, Reversal Symmetric, and Condorcet-Consistent Single-Winner Election Method by Markus Schulze (en inglés)
• Free Riding and Vote Management under Proportional Representation by the Single Transferable Vote by Markus Schulze (en inglés)
• Implementing the Schulze STV Method by Markus Schulze (en inglés)
• A New MMP Method by Markus Schulze (en inglés)
• A New MMP Method (Part 2) by Markus Schulze (en inglés)

• Datos: Q113
• Multimedia: Schulze method / Q113