Formato en coma flotante de media precisión
formato numérico de 16 bits De Wikipedia, la enciclopedia libre
En computación, la media precisión (a veces llamada FP16 o float16) es un formato de número de computadora de punto flotante binario que ocupa 16 bits (dos bytes en las computadoras modernas) en la memoria de la computadora. Está destinado al almacenamiento de valores de punto flotante en aplicaciones donde no es esencial una mayor precisión, en particular, el procesamiento de imágenes y las redes neuronales.
Casi todos los usos modernos siguen el estándar IEEE 754-2008, donde el formato base-2 de 16 bits se conoce como binary16 y el exponente usa 5 bits. Este puede expresar valores en el rango de ±65.504, siendo el valor mínimo por encima de 1 1 + 1/1024.
Dependiendo de la computadora, la precisión media puede ser un orden de magnitud más rápida que la precisión doble, por ejemplo, 550 PFLOPS para precisión media frente a 37 PFLOPS para doble precisión en un proveedor de nube.[1]
Han existido varios formatos anteriores de coma flotante de 16 bits, incluido el de Hitachi HD61810 DSP[2] de 1982, el WIF de Scott[3] y el procesador de gráficos 3dfx Voodoo.[4]
ILM estaba buscando un formato de imagen que pudiera manejar un amplio rango dinámico, pero sin el costo de disco duro y memoria del punto flotante de precisión simple o doble.[5] El grupo de sombreado programable acelerado por hardware dirigido por John Airey en SGI (Silicon Graphics) inventó el tipo de datos s10e5 en 1997 como parte del esfuerzo de diseño 'bali'. Esto se describe en un documento SIGGRAPH 2000[6] (consulte la sección 4.3) y se documenta más en la patente de EE. UU. 7518615.[7] Fue popularizado por su uso en el formato de imagen OpenEXR de código abierto.
Nvidia y Microsoft definieron el tipo de datos medio en el lenguaje Cg, lanzado a principios de 2002, y lo implementaron en silicio en GeForce FX, lanzado a finales de 2002.[8] Desde entonces, la compatibilidad con las matemáticas de coma flotante de 16 bits en las tarjetas gráficas se ha vuelto muy común.
La extensión F16C en 2012 permite que los procesadores x86 conviertan flotadores de precisión media a y desde flotadores de precisión simple con una instrucción de máquina.
El estándar IEEE 754[9] especifica un binario16 con el siguiente formato:
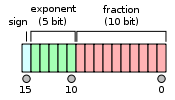
- Bit de signo: 1 bit
- Ancho del exponente: 5 bits
- Precisión significativa: 11 bits (10 almacenados explícitamente)
El formato se presenta de la siguiente manera:
Se supone que el formato tiene un bit inicial implícito con valor 1 a menos que el campo de exponente se almacene con todos ceros. Por lo tanto, solo aparecen 10 bits de la mantisa en el formato de memoria, pero la precisión total es de 11 bits. En el lenguaje IEEE 754, hay 10 bits de significado, pero hay 11 bits de precisión de significado (log 10 (211) ≈ 3.311 dígitos decimales, o 4 dígitos ± un poco menos de 5 unidades en el último lugar).
Codificación de exponentes
El exponente de punto flotante binario de precisión media se codifica utilizando una representación binaria compensada, siendo el desplazamiento cero 15; también conocido como sesgo de exponente en el estándar IEEE 754.
- Emín = 00001 2 − 01111 2 = −14
- E máx = 11110 2 − 01111 2 = 15
- Sesgo de exponente = 01111 2 = 15
Por lo tanto, como lo define la representación binaria compensada, para obtener el verdadero exponente, se debe restar la compensación de 15 del exponente almacenado.
Los exponentes almacenados 00000 2 y 11111 2 se interpretan de forma especial.
| Exponente | Significando = cero | Significando ≠ cero | Ecuación |
|---|---|---|---|
| 00000 2 | cero, −0 | números subnormales | (−1) bit de signo × 2 −14 × 0.bits significativos 2 |
| 00001 2, ..., 11110 2 | valor normalizado | (−1) signbit × 2 exponente−15 × 1.significantbits 2 | |
| 11111 2 | ± infinito | NaN (silencio, señalización) | |
El valor mínimo estrictamente positivo (subnormal) es 2 −24 ≈ 5,96 × 10 −8 . El valor normal positivo mínimo es 2 −14 ≈ 6,10 × 10 −5 . El valor máximo representable es (2−2 −10 ) × 2 15 = 65504.
Ejemplos de media precisión
Estos ejemplos se dan en representación de bits del valor de coma flotante. Esto incluye el bit de signo, el exponente (sesgado) y la significancia.
| Binario | Hexadecimal | Valor | Notas |
|---|---|---|---|
| 0 00000 0000000000 | 0000 | 0 | |
| 0 00000 0000000001 | 0001 | 2−14 × (0 + 11024 ) ≈ 0.000000059604645 | número subnormal positivo más pequeño |
| 0 00000 1111111111 | 03ff | 2−14 × (0 + 10231024 ) ≈ 0.000060975552 | número subnormal más grande |
| 0 00001 0000000000 | 0400 | 2−14 × (1 + 01024 ) ≈ 0.00006103515625 | número normal positivo más pequeño |
| 0 01101 0101010101 | 3555 | 2−2 × (1 + 3411024 ) ≈ 0.33325195 | valor más cercano a 1/3 |
| 0 01110 1111111111 | 3bff | 2−1 × (1 + 10231024 ) ≈ 0.99951172 | número mayor menor que uno |
| 0 01111 0000000000 | 3c00 | 20 × (1 + 01024 ) = 1 | uno |
| 0 01111 0000000001 | 3c01 | 20 × (1 + 11024 ) ≈ 1.00097656 | número más pequeño mayor que uno |
| 0 11110 1111111111 | 7bff | 215 × (1 + 10231024 ) = 65504 | número normal más grande |
| 0 11111 0000000000 | 7c00 | ∞ | infinito |
| 1 00000 0000000000 | 8000 | −0 | |
| 1 10000 0000000000 | c000 | -2 | |
| 1 11111 0000000000 | fc00 | −∞ | infinito negativo |
Por defecto, 1/3 redondea hacia abajo como para doble precisión, debido al número impar de bits en la mantisa. Los bits más allá del punto de redondeo son0101 ... que es menos de 1/2 de unidad en el último lugar.
Limitaciones de precisión
| Mín. | Máx. | Intervalo |
|---|---|---|
| 0 | 2 −13 | 2 −24 |
| 2 −13 | 2 −12 | 2 −23 |
| 2 −12 | 2 −11 | 2 −22 |
| 2 −11 | 2 −10 | 2 −21 |
| 2 −10 | 2 −9 | 2 −20 |
| 2 −9 | 2 −8 | 2 −19 |
| 2 −8 | 2 −7 | 2 −18 |
| 2 −7 | 2 −6 | 2 −17 |
| 2 −6 | 2 −5 | 2 −16 |
| 2 −5 | 2 −4 | 2 −15 |
| 2 −4 | 18 | 2 −14 |
| 18 | 14 | 2 −13 |
| 14 | 12 | 2 −12 |
| 12 | 1 | 2 −11 |
| 1 | 2 | 2 −10 |
| 2 | 4 | 2 −9 |
| 4 | 8 | 2 −8 |
| 8 | 16 | 2 −7 |
| 16 | 32 | 2 −6 |
| 32 | 64 | 2 −5 |
| 64 | 128 | 2 −4 |
| 128 | 256 | 18 |
| 256 | 512 | 14 |
| 512 | 1024 | 12 |
| 1024 | 2048 | 1 |
| 2048 | 4096 | 2 |
| 4096 | 8192 | 4 |
| 8192 | 16384 | 8 |
| 16384 | 32768 | 16 |
| 32768 | 65519 | 32 |
| 65519 | ∞ | ∞ |
65519 es el número más grande que se redondeará a un número finito (65504), 65520 y mayores se redondearán a infinito. Esto es para redondeo a par, otras estrategias de redondeo cambiarán este límite.
Los procesadores ARM admiten (a través de un bit de registro de control de punto flotante) un formato de "media precisión alternativa", que elimina el caso especial de un valor de exponente de 31 (11111 2 ).[10] Es casi idéntico al formato IEEE, pero no hay codificación para infinito o NaN; en cambio, un exponente de 31 codifica números normalizados en el rango de 65536 a 131008.
Este formato se utiliza en varios entornos de gráficos por computadora para almacenar píxeles, incluidos MATLAB, OpenEXR, JPEG XR, GIMP, OpenGL, Vulkan, Cg, Direct3D y D3DX. La ventaja sobre los enteros de 8 o 16 bits es que el mayor rango dinámico permite conservar más detalles en las luces y sombras de las imágenes, y la representación lineal de la intensidad facilita los cálculos. La ventaja sobre el punto flotante de precisión simple de 32 bits es que requiere la mitad del almacenamiento y el ancho de banda (a expensas de la precisión y el rango).[5]
El hardware y el software para el aprendizaje automático o las redes neuronales tienden a utilizar la mitad de la precisión: estas aplicaciones suelen realizar una gran cantidad de cálculos, pero no requieren un alto nivel de precisión.
Si el hardware tiene instrucciones para calcular matemáticas de precisión media, a menudo es más rápido que la precisión simple o doble. Si el sistema tiene instrucciones SIMD que pueden manejar múltiples números de coma flotante dentro de una instrucción, la precisión media puede ser el doble de rápida al operar con el doble de números simultáneamente.[11]
Varias versiones de la arquitectura ARM tienen soporte para media precisión.[12]
La compatibilidad con la precisión media en el conjunto de instrucciones x86 se especifica en la extensión del conjunto de instrucciones AVX-512_FP16 que se implementará en el futuro procesador Intel Sapphire Rapids.[13]
- Formato de coma flotante bfloat16: Formato alternativo de punto flotante de 16 bits con 8 bits de exponente y 7 bits de mantisa
- Minifloat: pequeños formatos de punto flotante
- IEEE 754: Estándar IEEE para aritmética de coma flotante (IEEE 754)
- ISO/IEC 10967, Aritmética independiente del lenguaje
- Tipo de dato elemental
- Formato de imagen RGBE
- Bus de administración de energía § Formato de coma flotante Linear11
- Formato en coma flotante de simple precisión
- Formato en coma flotante de doble precisión
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
