Atmósfera Estándar Internacional

La Atmósfera Estándar Internacional (del inglés: International Standard Atmosphere), más conocida por sus siglas ISA, es un modelo de la atmósfera terrestre que permite obtener los valores de presión, temperatura, densidad y viscosidad del aire en función de la altitud. Su función es proporcionar un marco de referencia invariante para la navegación aérea y para la realización de cálculos aerodinámicos consistentes.

La Atmósfera Estándar Internacional es un estándar de la ISO 2533:1975.^[1] Otros organismos como la Organización de Aviación Civil Internacional publican extensiones del mismo modelo bajo su propia autoridad de estandarización.

Perfil térmico vertical de la Atmósfera Estándar Internacional.

Descripción

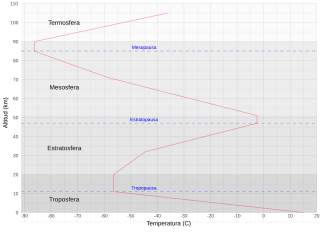
El modelo de la ISA divide la atmósfera en capas con distribuciones lineales de temperatura y se basa en condiciones promedio en latitudes medias.^[2] Estas han sido revisadas en varias ocasiones desde mediados del siglo XX.

A partir de los valores al nivel del mar, el resto de valores se obtienen mediante relaciones físicas básicas. Por tanto, el estándar consta de una tabla de valores para varias altitudes clave, además de varias fórmulas con las que se pueden calcular los valores para altitudes intermedias.^[3][4]

International Standard Atmosphere 1976

#	Capa	Altura geopotencial h0 (m s. n. m.)	Altura geométrica z0 (m s. n. m.)	Gradiente térmico a (K/km)	Temperatura base T0 (K)	Presión base p0 (Pa)	Densidad base ρ0 (kg/m3)
1	Troposfera	0,0	0,0	−6,5	288,15	101 325	1.2250
2	Tropopausa	11 000	11 019	0.0	216,65	22 632	0.3639
3	Estratosfera	20 000	20 063	+1,0	216,65	5474,9	0.0880
4	Estratosfera	32 000	32 162	+2,8	228,65	868,02	0.0132
5	Estratopausa	47 000	47 350	0.0	270,65	110,91	0.0020
6	Mesosfera	51 000	51 413	−2,8	270,65	66,939
7	Mesosfera	71 000	71 802	−2,0	214,65	3,9564
8	Mesopausa	84 852	86 000	0,0	186,87	0,3734

En la tabla superior, la altura geopotencial se calcula considerando que la aceleración de la gravedad es constante. La altura geométrica resulta de la suposición de que la gravedad disminuye con el cuadrado de la altitud.^[5]

Modelo matemático

Las diferentes magnitudes físicas del aire están relacionadas por la ley de los gases ideales:

${\displaystyle p=\rho RT}$, donde

• ${\displaystyle p}$ es la presión atmosférica.
• ${\displaystyle \rho }$ es la densidad del aire.
• ${\displaystyle R}$ es la constante individual del aire, cuyo valor es ${\displaystyle R=287{\begin{bmatrix}{\frac {m^{2}}{s^{2}\cdot K}}\end{bmatrix}}}$
• ${\displaystyle T}$ es la temperatura del aire.

Por otra parte, la presión se debe al peso de las capas de aire por encima de la altitud considerada, de modo que la variación de presión puede expresarse como:

${\displaystyle {\frac {dp}{dh}}=-\rho g}$, donde

• ${\displaystyle h}$ es la altitud.
• ${\displaystyle g}$ es la aceleración de la gravedad.

En el modelo de la ISA se utiliza una aceleración de la gravedad constante igual a su valor al nivel del mar (g=9,80665 m/s²). En realidad la aceleración de la gravedad disminuye con la altitud, por lo que los valores calculados no corresponden con la altitud geométrica ${\displaystyle z}$, sino con la altitud geopotencial ${\displaystyle h}$. Se puede convertir de una a otra mediante la relación:

${\displaystyle z={\frac {R_{e}\cdot h}{R_{e}-h}}}$, donde ${\displaystyle R_{e}}$ es el radio de la Tierra.

Para poder derivar los valores físicos de la atmósfera a partir de las ecuaciones anteriores, es preciso establecer unos valores iniciales de presión, temperatura y densidad, además de un perfil de gradientes de temperatura en función de la altitud. La ISA establece una serie de franjas de altitud en las que la temperatura varía linealmente con un gradiente térmico constante. A partir de esta suposición, se pueden obtener expresiones para las magnitudes deseadas, distinguiendo dos casos:

gradiente ${\displaystyle a=0}$	gradiente ${\displaystyle a\neq 0}$
${\displaystyle T(h)=T_{0}}$	${\displaystyle T(h)=T_{0}+a\cdot (h-h_{0})}$
${\displaystyle p(h)=p_{0}\cdot e^{-{\frac {g}{RT}}\cdot (h-h_{0})}}$	${\displaystyle p(h)=p_{0}{\left({\frac {T(h)}{T_{0}}}\right)}^{-{\frac {g}{aR}}}}$
${\displaystyle \rho (h)=\rho _{0}\cdot e^{-{\frac {g}{RT}}\cdot (h-h_{0})}}$	${\displaystyle \rho (h)=\rho _{0}{\left({\frac {T(h)}{T_{0}}}\right)}^{-1-{\frac {g}{aR}}}}$

donde ${\displaystyle h_{0},p_{0},\rho _{0}\ y\ T_{0}}$ son los valores en la base de la franja considerada.

Véase también

• Atmósfera terrestre
• Ecuación fundamental de la fluidoestática
• Ecuación hipsométrica

Referencias

1. «ISO 2533:1975 Standard Atmosphere». International Standard Organisation. Consultado el 18 de abril de 2014.
2. Gyatt, Graham (26 de marzo de 2011). «The Standard Atmosphere. A mathematical model of the 1976 U.S. Standard Atmosphere». Archivado desde el original el 10 de marzo de 2007. Consultado el 18 de abril de 2014.
3. Auld, D.J.; Srinivas, K. (2008). «Properties of the Atmosphere». Archivado desde el original el 9 de junio de 2013. Consultado el 13 de marzo de 2008.
4. Batchelor, G. K. (1967). An Introduction to Fluid Dynamics. Cambridge Univ. Press.
5. «Атмосфера Стандартная» (en ruso). Consultado el 21 de agosto de 2015.

• Datos: Q579176
• Multimedia: International Standard Atmosphere / Q579176