Cinética de Michaelis-Menten

La cinética de Michaelis-Menten describe la velocidad de reacción de muchas reacciones enzimáticas. Recibe este nombre en honor a Leonor Michaelis y Maude Menten. Este modelo sólo es válido cuando la concentración del sustrato es mayor que la concentración de la enzima, y para condiciones de estado estacionario, es decir, cuando la concentración del complejo enzima-sustrato es constante.

Determinación de constantes

Para determinar la velocidad máxima de una reacción enzimática, la concentración de sustrato ([S]) se aumenta hasta alcanzar una velocidad constante de formación de producto. Esa es la velocidad máxima (V_max) de la enzima. En ese caso los sitios activos de la enzima están saturados con sustrato.

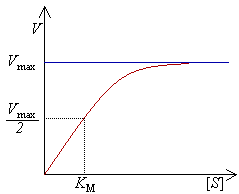
Diagrama de velocidad de reacción y constante de Michaelis-Menten.

Velocidad de reacción

La velocidad V indica el número de moléculas del sustrato que se convierten en producto por segundo. Con concentraciones crecientes de sustrato[S], la enzima va acercándose asintóticamente a su velocidad máxima V_max, pero nunca la alcanza. Por esta razón, no hay un valor de [S] determinado para la V_max. De todas formas, se puede definir un parámetro característico de la enzima empleando la concentración de sustrato a la cual se alcanza la mitad de la velocidad máxima (V_max/2). Podemos resumir el significado de V_max con las siguientes afirmaciones:^[1][2]

• Corresponde al límite superior de la velocidad de reacción.
• Equivale al producto kcat*[E]t
• Permite inferir la concentración de enzima inicial
• Se obtiene gráficamente
• Graficando v vs. [S] es difícil encontrar V manualmente, por lo que se necesita usar un método de ajuste no lineal de los puntos experimentales.

Constante de Michaelis-Menten

Artículo principal: Constante de Michaelis

Aunque es imposible medir exactamente la concentración de sustrato que da V_max, las enzimas pueden caracterizarse mediante la concentración de sustrato a la cual la velocidad de reacción es la mitad de la velocidad máxima. Esta concentración de sustrato se conoce como constante de Michaelis-Menten (K_M). Para enzimas que exhiben una cinética de Michaelis-Menten simple esta constante representa la constante de disociación del complejo enzima-sustrato (ES) (o la inversa de la afinidad entre enzima y sustrato). Valores bajos indican que el complejo ES está unido muy fuertemente y raramente se disocia sin que el sustrato reaccione para dar producto. En estos casos se obtendrá una K_M diferente según el sustrato específico sobre el que actúe la enzima (como sucede en el caso de enzimas que actúan sobre sustratos análogos) y según las condiciones de reacción en que se realicen las mediciones.^[3]

El significado de km se puede resumir en las siguientes afirmaciones:^[1][2]

• Se expresa en unidades de concentración
• Numéricamente corresponde a la concentración a la que se alcanza el 50% de saturación de la enzima
• Está relacionada con la afinidad, es decir, la fuerza de unión entre la enzima y su sustrato. Valores grandes de km significan poca afinidad, mientras que valores pequeños de km (usualmente menores al rango milimolar) corresponden a una afinidad alta de la enzima por el sustrato.
• Es una constante aparente de disociación del complejo enzima - sustrato (E·S).

Nota: K_M solo se puede usar para determinar la afinidad de una enzima por un sustrato, k₂ es limitante de la velocidad, por ejemplo, si k₂ << k_-1 y K_M se convierte en k_-1/k₁. Generalmente, k₂ >> k_-1 o bien k₂ y k_-1 son comparables.

Ecuación

La derivación de Michaelis y Menten está descrita por Briggs y Haldane. Se obtiene de la siguiente manera:

Se supone que la reacción enzimática es irreversible, y que el producto no se liga con la enzima después de la reacción.

${\displaystyle E+S{\begin{matrix}k_{1}\\\longrightarrow \\\longleftarrow \\k_{-1}\end{matrix}}ES{\begin{matrix}k_{2}\\\longrightarrow \\\ \end{matrix}}E+P}$

Siguiendo la aproximación del estado estacionario, que señala que la concentración del complejo enzima-sustrato (${\displaystyle ES}$) es pequeña y se mantiene casi constante a lo largo de la reacción enzimática:

${\displaystyle {\frac {d[ES]}{dt}}=k_{1}[E][S]-k_{-1}[ES]-k_{2}[ES]=0}$

${\displaystyle [ES]={\frac {k_{1}[E][S]}{k_{-1}+k_{2}}}}$

Se define:

${\displaystyle K_{m}={\frac {k_{-1}+k_{2}}{k_{1}}}}$

Entonces:

${\displaystyle [ES]={\frac {[E][S]}{K_{m}}}}$ (1)

La velocidad de reacción es:

${\displaystyle {\frac {d[P]}{dt}}=k_{2}[ES]}$ (2)

La concentración total de la enzima:

${\displaystyle [E_{0}]=[E]+[ES]}$

Por lo tanto:

${\displaystyle [E]=[E_{0}]-[ES]}$ (3)

Sustituyendo (3) en (1) da:

${\displaystyle [ES]={\frac {([E_{0}]-[ES])[S]}{K_{m}}}}$

Reordenando:

${\displaystyle K_{m}[ES]+[S][ES]=[E_{0}][S]}$

${\displaystyle [ES]={\frac {[E_{0}][S]}{K_{m}+[S]}}}$ (4)

Sustituyendo (4) en (2) :

${\displaystyle {\frac {d[P]}{dt}}=k_{2}[E_{0}]{\frac {[S]}{K_{m}+[S]}}=V_{max}{\frac {[S]}{K_{m}+[S]}}}$

Esta ecuación se puede analizar experimentalmente con un diagrama de Lineweaver-Burke, un diagrama de Eadie-Hofstee o un diagrama de Hanes-Woolf.

• ${\displaystyle E_{0}}$ es el total de enzima. No es práctico medir la cantidad de complejo enzima-sustrato durante la reacción, por lo que debe escribirse ésta en términos de cantidad total o inicial de enzima, que es una cantidad conocida.
• ${\displaystyle d[P]/dt}$ o ${\displaystyle V_{0}}$ es la velocidad de formación del producto.
• ${\displaystyle k_{2}[E_{0}]}$ o ${\displaystyle V_{max}}$ es la velocidad máxima. k₂ se denomina con frecuencia k_cat.

Cabe observar que [S] es grande comparada con K_m, [S]/(K_m + [S]) tiende a 1. La velocidad de formación de producto es igual a k₂[E₀] en ese caso.

Cuando [S] es igual a K_m, [S]/(K_m + [S]) vale 0.5. En ese caso, la velocidad de formación de producto es la mitad de la máxima (1/2 V_max). Representando gráficamente V₀ frente a [S] se puede fácilmente determinar V_max y K_m. Esto requiere una serie de experimentos a E₀ constante y diferentes concentraciones de sustrato [S].

Cómo se construye la gráfica

La gráfica de Michaelis - Menten se construye a partir de las velocidades iniciales de reacción de distintas concentraciones de sustrato obtenidas en un ensayo enzimático. El procedimiento a seguir es el siguiente:^[4]

1. Obtener la velocidad inicial de reacción (V) para cada concentración de sustrato a partir de los datos de un ensayo enzimático.
2. Tabular los valores de V para cada concentración de sustrato [S].
3. Elaborar una gráfica de dispersión de V vs. [S].
4. Trazar una curva hiperbólica desde el origen y extender la curva hacia valores mayores de [S].
5. Analizar por inspección la tendencia de la curva. La curva debe mostrar un comportamiento asintótico hacia un límite superior de la velocidad. Este valor límite es V_max. Teóricamente Vmax es la velocidad inicial de reacción cuando [S] tiende a infinito.
6. Sobre el eje de las abscisas, encontrar V_max y dividir este valor entre 2.
7. Encontrar por interpolación el valor de [S] que corresponde a 1/2 de V_max. Este valor de concentración es K_m.

Fuentes

• Catalysis chapter from the Biochemistry textbook released under the GFDL

Referencias

1. Van Holde, K. E.; Ahern, Kevin G.; González de Buitrago, José Manuel (2002). Bioquímica. Addison Wesley. ISBN 84-7829-053-2. OCLC 53317350. Consultado el 8 de noviembre de 2021.
2. Copeland, Robert Allen (2000). Enzymes : a practical introduction to structure, mechanism, and data analysis (2nd ed edición). Wiley. ISBN 0-471-35929-7. OCLC 42619660. Consultado el 8 de noviembre de 2021.
3. Nelson, David L.; Cox, Michael M. (D.L. 1995). Principios de bioquímica (2{487} ed., 1{487} reimp. corr edición). Omega. ISBN 84-282-0924-3. OCLC 627344066. Consultado el 8 de noviembre de 2021.
4. Cornish-Bowden, Athel (2012). Fundamentals of enzyme kinetics (4th ed., rev. and enlarged edición). Wiley-VCH. ISBN 978-3-527-33074-4. OCLC 778269108. Consultado el 8 de noviembre de 2021.

• Datos: Q613955
• Multimedia: Michaelis–Menten kinetics / Q613955