From Wikipedia, the free encyclopedia
Pri la aliaj signifoj de koniko rigardu en Koniko (apartigilo).


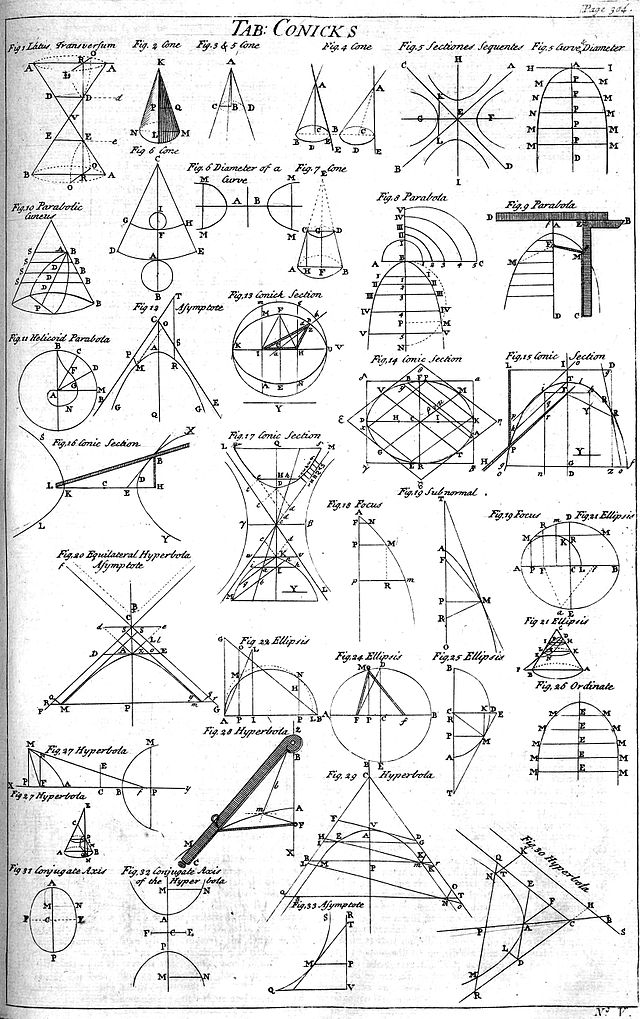
En matematiko, koniko estas unu-dimensia lokaro de punktoj produktata de la intersekco de ebeno kaj konuso. La konikoj estis nomitaj kaj studitaj ĉirkaŭ 200 a.K., kiam Apolonio de Pergo faris sisteman studon de iliaj trajtoj.
Ne degenera koniko estas unu el cirklo, elipso, parabolo, hiperbolo.
Koniko havas kontinue kreskantan aŭ malkreskantan kurbecon (glata linio); pli detale, ĝi havas neniun trafleksan punkton.
Estas multaj degeneraj okazoj, en kiu la ebeno pasas tra la apekso de la konuso. La komunaĵo en ĉi tiuj okazoj povas esti:
Se la konuso estas degenera cilindro (la vertico estas je malfinio), la cilindraj sekcoj estas ricevataj. Ĉi tio povas esti:

Ĉiu koniko povas esti difinita per fiksa punkto F (la fokuso), linio L (la direktanto) ne enhavanta punkton F kaj nenegativa reela nombro e (la discentreco). La respektiva koniko konsistas el ĉiuj punktoj kies distanco al F egalas al distanco al L multiplikita je e.
Por elipso kaj hiperbolo, du fokuso-direktantaj kombinaĵoj povas esti prenita, ĉiu donante la saman plenan figuron.
La distanco de la centro al la direktanto estas a/e, kie a estas la granda duonakso de la elipso, aŭ la distanco de la centro al la suproj de la hiperbolo. La distanco de la centro al fokuso estas ae.
Ĉe cirklo kun la discentreco e=0, oni povas imagi ke la direktanto estas malfinie malproksima de la centro. Tamen, la frazo ke la cirklo konsistas el ĉiuj punktoj kies distanco estas e fojoj la distanco al L estas neutila, ĉar oni prenas nulon da fojoj malfinion.
La discentreco de koniko estas tial mezuro de tio kiel malsimila ĝi estas de cirklo.
Por donita a, ju pli proksima e estas al 1, des la pli malgranda estas la malgranda duonakso.
En la karteziaj koordinatoj, la grafikaĵo de kvadrata ekvacio de du variabloj estas ĉiam koniko, kaj ĉiuj koniko povas esti prezentita tiel. La ekvacio estas de formo
Tiam:
Per ŝanĝi de koordinatoj (movo aŭ turno) ĉi tiuj ekvacioj povas esti konvertitaj en la normajn formojn:
La figuroj povas esti skribita kiel parametraj ekvacioj:
Diversaj parametroj povas esti asociita kun koniko (estas prenite ke a>b).
| Nomo | Ekvacio | Discentreco e | Lineara discentreco c | Duono de flanka streko l | Parametro p |
|---|---|---|---|---|---|
| Cirklo | x2+y2 = r2 | 0 | 0 | r | |
| Elipso | |||||
| Parabolo | y2=4ax | 1 | a | 2a | 2a |
| Hiperbolo |
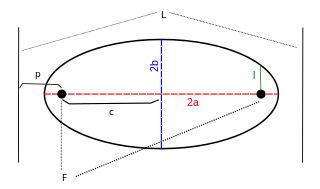
La lineara discentreco c estas distanco inter la centro kaj la fokuso.
La flanka streko 2l estas la ĥordo paralela al la direktanto kaj pasanta tra la fokuso.
La fokusa parametro p estas la distanco de la fokuso al la direktanto, p = l/e.
En polusaj koordinatoj, koniko kun unu fokuso je la fonto kaj la alia fokuso sur la x-akso, estas donita per la ekvacio
kie e estas la discentreco kaj l= e.p.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.