Ĉi tiu artikolo priskribas la kvar malfiniajn seriojn de punktaj grupoj en tri dimensioj (n≥1) kun n-obla turna simetrio ĉirkaŭ unu akso (turnado per angulo de 360°/n ne ŝanĝas la objekton), sen la aliaj turnaj simetrioj (n=1 estas okazo sen ajna turna simetrio).
- Cn (nn) de ordo n - n-obla turna simetrio (abstrakta grupo cikla grupo Cn); por n=1: ne simetria (triviala grupo)
Memspegulsimetria:
- Cnh (n*) de ordo 2n - prisma simetrio (abstrakta grupo duedra grupo Dn × C2); por n=1 ĉi tiu estas skribata kiel Cs (1*) kaj estas la reflekta simetrio, aŭ ambaŭflanka simetrio en biologio.
- Cnv (*nn) de ordo 2n - piramida simetrio (abstrakta grupo Dn); en biologio C2v estas nomata kiel duradia simetrio. Por n=1 ĝi denove estas la samo kiel Cs (1*).
- S2n (n×) de ordo 2n (devas ne esti konfuzita kun simetriaj grupoj, por kiu la sama skribmaniero estas uzita; abstrakta grupo C2n); por n=1 ĝi estas S2 (1×), ankaŭ skribata kiel Ci; ĉi tiu estas inversiga simetrio
Ili estas la finiaj geometriaj simetriaj grupoj sur konuso. Por n = ili estas konformaj laŭ kvar frisaj grupoj.
Pli sube estas uzata notacio de Arthur Moritz Schönflies, kaj en krampoj notacio de Conway. La terminoj horizontalo kaj vertikalo estas uzataj kun respektivo al vertikala rotacia akso.
Cnh (n*) havas reflektan simetrion kun respektivo al ebeno perpendikulara al la n-obla turnada akso.
Cnv (*nn) havas vertikalajn spegulajn ebenojn. Ĉi tiu estas la geometria simetria grupo por regula n-flankita piramido.
S2n (n×) havas 2n-oblan turnoreflektan akson, ankaŭ nomatan kiel 2n-obla nepropra turnada akso, kio estas, la geometria simetria grupo enhavas kombinaĵo de reflekto en la horizontala ebeno kaj turnado per angulo 180°/n. Tial, simile al Dnd, ĝi enhavas certan kvanton de nepropraj turnadoj sen enhavo de la respektivaj turnadoj.
C2h (2*) kaj C2v (*22) de ordo 4 estas du el la tri specoj de 3-dimensiaj geometriaj simetriaj grupoj kun la kvar-grupo de Klein kiel abstrakta grupo. C2v aplikas ekzemple por ortangula kahelo kun ĝia supro malsama de ĝia fundo.
 Paralelepipedo S2/Ci (1x) |
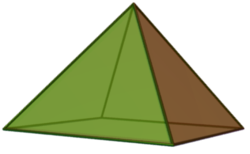 Kvadrata piramido C4v (*44) |
 Plilongigita kvadrata piramido C4v (*44) |
 Kvinlatera piramido C5v (*55) |
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
