Loading AI tools
Objects sharing the orbit of a larger one From Wikipedia, the free encyclopedia
In astronomy, a trojan is a small celestial body (mostly asteroids) that shares the orbit of a larger body, remaining in a stable orbit approximately 60° ahead of or behind the main body near one of its Lagrangian points L4 and L5. Trojans can share the orbits of planets or of large moons.
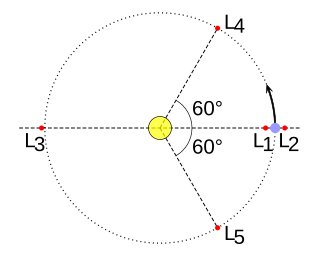
Trojans are one type of co-orbital object. In this arrangement, a star and a planet orbit about their common barycenter, which is close to the center of the star because it is usually much more massive than the orbiting planet. In turn, a much smaller mass than both the star and the planet, located at one of the Lagrangian points of the star–planet system, is subject to a combined gravitational force that acts through this barycenter. Hence the smallest object orbits around the barycenter with the same orbital period as the planet, and the arrangement can remain stable over time.[1]
In the Solar System, most known trojans share the orbit of Jupiter. They are divided into the Greek camp at L4 (ahead of Jupiter) and the Trojan camp at L5 (trailing Jupiter). More than a million Jupiter trojans larger than one kilometer are thought to exist,[2] of which more than 7,000 are currently catalogued. In other planetary orbits only nine Mars trojans, 31 Neptune trojans, two Uranus trojans, and two Earth trojans, have been found to date. A temporary Venus trojan is also known. Numerical orbital dynamics stability simulations indicate that Saturn probably does not have any primordial trojans.[3]
The same arrangement can appear when the primary object is a planet and the secondary is one of its moons, whereby much smaller trojan moons can share its orbit. All known trojan moons are part of the Saturn system. Telesto and Calypso are trojans of Tethys, and Helene and Polydeuces of Dione.

| Jupiter trojans | Asteroid belt | Hilda asteroids |
In 1772, the Italian–French mathematician and astronomer Joseph-Louis Lagrange obtained two constant-pattern solutions (collinear and equilateral) of the general three-body problem.[4] In the restricted three-body problem, with one mass negligible (which Lagrange did not consider), the five possible positions of that mass are now termed Lagrange points.
The term "trojan" originally referred to the "trojan asteroids" (Jovian trojans) that orbit close to the Lagrangian points of Jupiter. These have long been named for figures from the Trojan War of Greek mythology. By convention, the asteroids orbiting near the L4 point of Jupiter are named for the characters from the Greek side of the war, whereas those orbiting near the L5 of Jupiter are from the Trojan side. There are two exceptions, named before the convention was adopted: 624 Hektor in the L4 group, and 617 Patroclus in the L5 group.[5]
Astronomers estimate that the Jovian trojans are about as numerous as the asteroids of the asteroid belt.[6]
Later on, objects were found orbiting near the Lagrangian points of Neptune, Mars, Earth,[7] Uranus, and Venus. Minor planets at the Lagrangian points of planets other than Jupiter may be called Lagrangian minor planets.[8]
| Planet | Number in L4 | Number in L5 | List (L4) | List (L5) |
|---|---|---|---|---|
| Mercury | 0 | 0 | — | — |
| Venus | 1 | 0 | 2013 ND15 | — |
| Earth | 2 | 0 | (706765) 2010 TK7, (614689) 2020 XL5 | — |
| Mars | 1 | 13 | (121514) 1999 UJ7 | many |
| Jupiter | 7508 | 4044 | many | many |
| Saturn | 1 | 0 | 2019 UO14 | — |
| Uranus | 2 | 0 | (687170) 2011 QF99, (636872) 2014 YX49 | — |
| Neptune | 24 | 4 | many | many |
Whether or not a system of star, planet, and trojan is stable depends on how large the perturbations are to which it is subject. If, for example, the planet is the mass of Earth, and there is also a Jupiter-mass object orbiting that star, the trojan's orbit would be much less stable than if the second planet had the mass of Pluto.
As a rule of thumb, the system is likely to be long-lived if m1 > 100m2 > 10,000m3 (in which m1, m2, and m3 are the masses of the star, planet, and trojan).
More formally, in a three-body system with circular orbits, the stability condition is 27(m1m2 + m2m3 + m3m1) < (m1 + m2 + m3)2. So the trojan being a mote of dust, m3→0, imposes a lower bound on m1/m2 of 25+√621/2 ≈ 24.9599. And if the star were hyper-massive, m1→+∞, then under Newtonian gravity, the system is stable whatever the planet and trojan masses. And if m1/m2 = m2/m3, then both must exceed 13+√168 ≈ 25.9615. However, this all assumes a three-body system; once other bodies are introduced, even if distant and small, stability of the system requires even larger ratios.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.