Nuclear fusion
Process of combining atomic nuclei From Wikipedia, the free encyclopedia
Nuclear fusion is a reaction in which two or more atomic nuclei combine to form a larger nuclei, nuclei/neutron by-products. The difference in mass between the reactants and products is manifested as either the release or absorption of energy. This difference in mass arises as a result of the difference in nuclear binding energy between the atomic nuclei before and after the fusion reaction. Nuclear fusion is the process that powers all active stars, via many reaction pathways.
From top, left to right
- The Sun, powered by the proton-proton fusion chain
- Antares, a star massive enough for silicon burning
- Castle Bravo, the largest US fusion weapon test
- Greenhouse George's Cylinder device, the first artificial thermonuclear fusion experiment
- Ivy Mike's Sausage device, the first Teller-Ulam bomb
- Fusion plasma in China's Experimental Advanced Superconducting Tokamak
- The National Ignition Facility, the world's largest inertial confinement fusion experiment
Fusion processes require an extremely large triple product of temperature, density, and confinement time. These conditions occur only in stellar cores, advanced nuclear weapons, and are approached in fusion power experiments.
A nuclear fusion process that produces atomic nuclei lighter than nickel-62 is generally exothermic, due to the positive gradient of the nuclear binding energy curve. The most fusible nuclei are among the lightest, especially deuterium, tritium, and helium-3. The opposite process, nuclear fission, is most energetic for very heavy nuclei, especially the actinides.
Applications of fusion include fusion power, thermonuclear weapons, boosted fission weapons, neutron sources, and superheavy element production.
History
Summarize
Perspective
Theory

American chemist William Draper Harkins was the first to propose the concept of nuclear fusion in 1915.[1] Francis William Aston's 1919 invention of the mass spectrometer allowed the discovery that four hydrogen atoms are heavier than one helium atom. Thus in 1920, Arthur Eddington correctly predicted fusion of hydrogen into helium could be the primary source of stellar energy.[2]
Quantum tunneling was discovered by Friedrich Hund in 1927, with relation to electron levels.[3][4] In 1928, George Gamow was the first to apply tunneling to the nucleus, first to alpha decay, then to fusion as an inverse process. From this, in 1929, Robert Atkinson and Fritz Houtermans made the first estimates for stellar fusion rates.[5][6]
In 1938, Hans Bethe worked with Charles Critchfield to enumerate the proton–proton chain that dominates Sun-type stars. In 1939, Bethe published the discovery of the CNO cycle common to higher-mass stars.
Early experiments

During the 1920s, Patrick Blackett made the first conclusive experiments in artificial nuclear transmutation at the Cavendish Laboratory. There, John Cockcroft and Ernest Walton built their generator on the inspiration of Gamow's paper. In April 1932, they published experiments on the reaction:
where the intermediary nuclide was later confirmed to be the extremely short-lived beryllium-8.[7] This has a claim to the first artificial fusion reaction.[citation needed]
In papers from July and November 1933, Ernest Lawrence et. al. at the University of California Radiation Laboratory, in some of the earliest cyclotron experiments, accidentally produced the first deuterium-deuterium fusion reactions:
- 2
1D
+ 2
1D
→ 3
1T
+ p - 2
1D
+ 2
1D
→ 3
2He
+ 1
0n
The Radiation Lab, only detecting the resulting energized protons and neutrons,[8][9] misinterpreted the source as an exothermic disintegration of the deuterons, now known to be impossible.[10] In May 1934, Mark Oliphant, Paul Harteck, and Ernest Rutherford at the Cavendish Laboratory,[11] published an intentional deuterium fusion experiment, and made the discovery of both tritium and helium-3. This is widely considered the first experimental demonstration of fusion.[10]
In 1938, Arthur Ruhlig at the University of Michigan made the first observation of deuterium–tritium (DT) fusion and its characteristic 14 MeV neutrons, now known as the most favourable reaction:
- 2
1D
+ 3
1T
→ 4
2He
+ 1
0n
Weaponization
Research into fusion for military purposes began in the early 1940s as part of the Manhattan Project. In 1941, Enrico Fermi and Edward Teller had a conversation about the possibility of a fission bomb creating conditions for thermonuclear fusion. In 1942, Emil Konopinski brought Ruhlig's work on the deuterium-tritium reaction to the projects attention. J. Robert Oppenheimer initially commissioned physicists at Chicago and Cornell to use the Harvard University cyclotron to secretly investigate its cross-section, and that of the lithium reaction (see below). Measurements were obtained at Purdue, Chicago, and Los Alamos from 1942-1946. Theoretical assumptions about DT fusion gave it a similar cross-section to DD. However, in 1946 Egon Bretscher discovered a resonance enhancement giving the DT reaction a cross-section ~100 times larger.[12]
From 1945, John von Neumann, Teller, and other Los Alamos scientists used ENIAC, one of the first electronic computers, to simulate thermonuclear weapon detonations.[13]
The first artificial thermonuclear fusion reaction occurred during the 1951 US Greenhouse George nuclear test, using a small amount of deuterium–tritium gas. This produced the largest yield to date, at 225 kt, 15 times that of Little Boy. The first "true" thermonuclear weapon detonation i.e. a two-stage device, was the 1952 Ivy Mike test of a liquid deuterium-fusing device, yielding over 10 Mt. The key to this jump was the full utilization of the fission blast by the Teller-Ulam design.
The Soviet Union had begun their focus on a hydrogen bomb program earlier, and in 1953 carried out the RDS-6s test. This had international impacts as the first air-deliverable bomb using fusion, but yielded 400 kt and was limited by its single-stage design. The first Soviet two-stage test was RDS-37 in 1955 yielding 1.5 Mt, using an independently-reached version of the Teller-Ulam design.
Modern devices benefit from the usage of solid lithium deuteride with an enrichment of lithium-6. This is due to the Jetter cycle involving the exothermic reaction:
- 6
3Li
+ 1
0n
→ 4
2He
+ 3
1T
During thermonuclear detonations, this provides tritium for the highly energetic DT reaction, and benefits from its neutron production, creating a closed neutron cycle.[14]
Fusion energy
While fusion bomb detonations were loosely considered for energy production, the possibility of controlled and sustained reactions remained the scientific focus for peaceful fusion power. Research into developing controlled fusion inside fusion reactors has been ongoing since the 1930s, with Los Alamos National Laboratory's Scylla I device producing the first laboratory thermonuclear fusion in 1958, but the technology is still in its developmental phase.[15]
The US National Ignition Facility, which uses laser-driven inertial confinement fusion, was designed with a goal of achieving a fusion energy gain factor (Q) of larger than one; the first large-scale laser target experiments were performed in June 2009 and ignition experiments began in early 2011.[16][17] On 13 December 2022, the United States Department of Energy announced that on 5 December 2022, they had successfully accomplished break-even fusion, "delivering 2.05 megajoules (MJ) of energy to the target, resulting in 3.15 MJ of fusion energy output."[18]
Prior to this breakthrough, controlled fusion reactions had been unable to produce break-even (self-sustaining) controlled fusion.[19] The two most advanced approaches for it are magnetic confinement (toroid designs) and inertial confinement (laser designs). Workable designs for a toroidal reactor that theoretically will deliver ten times more fusion energy than the amount needed to heat plasma to the required temperatures are in development (see ITER). The ITER facility is expected to finish its construction phase in 2025. It will start commissioning the reactor that same year and initiate plasma experiments in 2025, but is not expected to begin full deuterium–tritium fusion until 2035.[20]
Private companies pursuing the commercialization of nuclear fusion received $2.6 billion in private funding in 2021 alone, going to many notable startups including but not limited to Commonwealth Fusion Systems, Helion Energy Inc., General Fusion, TAE Technologies Inc. and Zap Energy Inc.[21]
One of the most recent breakthroughs to date in maintaining a sustained fusion reaction occurred in France's WEST fusion reactor. It maintained a 90 million degree plasma for a record time of six minutes. This is a tokamak style reactor which is the same style as the upcoming ITER reactor.[22]
Process
Summarize
Perspective

The release of energy with the fusion of light elements is due to the interplay of two opposing forces: the nuclear force, a manifestation of the strong interaction, which holds protons and neutrons tightly together in the atomic nucleus; and the Coulomb force, which causes positively charged protons in the nucleus to repel each other.[24] Lighter nuclei (nuclei smaller than iron and nickel) are sufficiently small and proton-poor to allow the nuclear force to overcome the Coulomb force. This is because the nucleus is sufficiently small that all nucleons feel the short-range attractive force at least as strongly as they feel the infinite-range Coulomb repulsion. Building up nuclei from lighter nuclei by fusion releases the extra energy from the net attraction of particles. For larger nuclei, however, no energy is released, because the nuclear force is short-range and cannot act across larger nuclei.
Fusion powers stars and produces most elements lighter than cobalt in a process called nucleosynthesis. The Sun is a main-sequence star, and, as such, generates its energy by nuclear fusion of hydrogen nuclei into helium. In its core, the Sun fuses 620 million metric tons of hydrogen and makes 616 million metric tons of helium each second. The fusion of lighter elements in stars releases energy and the mass that always accompanies it. For example, in the fusion of two hydrogen nuclei to form helium, 0.645% of the mass is carried away in the form of kinetic energy of an alpha particle or other forms of energy, such as electromagnetic radiation.[25]
It takes considerable energy to force nuclei to fuse, even those of the lightest element, hydrogen. When accelerated to high enough speeds, nuclei can overcome this electrostatic repulsion and be brought close enough such that the attractive nuclear force is greater than the repulsive Coulomb force. The strong force grows rapidly once the nuclei are close enough, and the fusing nucleons can essentially "fall" into each other and the result is fusion; this is an exothermic process.[26]
Energy released in most nuclear reactions is much larger than in chemical reactions, because the binding energy that holds a nucleus together is greater than the energy that holds electrons to a nucleus. For example, the ionization energy gained by adding an electron to a hydrogen nucleus is 13.6 eV—less than one-millionth of the 17.6 MeV released in the deuterium–tritium (D–T) reaction shown in the adjacent diagram. Fusion reactions have an energy density many times greater than nuclear fission; the reactions produce far greater energy per unit of mass even though individual fission reactions are generally much more energetic than individual fusion ones, which are themselves millions of times more energetic than chemical reactions. Via the mass–energy equivalence, fusion yields a 0.7% efficiency of reactant mass into energy. This can be only be exceeded by the extreme cases of the accretion process involving neutron stars or black holes, approaching 40% efficiency, and antimatter annihilation at 100% efficiency. (The complete conversion of one gram of matter would expel 9×1013 joules of energy.)
In astrophysics
Summarize
Perspective
Fusion is responsible for the astrophysical production of the majority of elements lighter than iron. This includes most types of Big Bang nucleosynthesis and stellar nucleosynthesis. Non-fusion processes that contribute include the s-process and r-process in neutron merger and supernova nucleosynthesis, responsible for elements heavier than iron.
Stars


An important fusion process is the stellar nucleosynthesis that powers stars, including the Sun. In the 20th century, it was recognized that the energy released from nuclear fusion reactions accounts for the longevity of stellar heat and light. The fusion of nuclei in a star, starting from its initial hydrogen and helium abundance, provides that energy and synthesizes new nuclei. Different reaction chains are involved, depending on the mass of the star (and therefore the pressure and temperature in its core).
Around 1920, Arthur Eddington anticipated the discovery and mechanism of nuclear fusion processes in stars, in his paper The Internal Constitution of the Stars.[27][28] At that time, the source of stellar energy was unknown; Eddington correctly speculated that the source was fusion of hydrogen into helium, liberating enormous energy according to Einstein's equation E = mc2. This was a particularly remarkable development since at that time fusion and thermonuclear energy had not yet been discovered, nor even that stars are largely composed of hydrogen (see metallicity). Eddington's paper reasoned that:
- The leading theory of stellar energy, the contraction hypothesis, should cause the rotation of a star to visibly speed up due to conservation of angular momentum. But observations of Cepheid variable stars showed this was not happening.
- The only other known plausible source of energy was conversion of matter to energy; Einstein had shown some years earlier that a small amount of matter was equivalent to a large amount of energy.
- Francis Aston had also recently shown that the mass of a helium atom was about 0.8% less than the mass of the four hydrogen atoms which would, combined, form a helium atom (according to the then-prevailing theory of atomic structure which held atomic weight to be the distinguishing property between elements; work by Henry Moseley and Antonius van den Broek would later show that nucleic charge was the distinguishing property and that a helium nucleus, therefore, consisted of two hydrogen nuclei plus additional mass). This suggested that if such a combination could happen, it would release considerable energy as a byproduct.
- If a star contained just 5% of fusible hydrogen, it would suffice to explain how stars got their energy. (It is now known that most 'ordinary' stars are usually made of around 70% to 75% hydrogen)
- Further elements might also be fused, and other scientists had speculated that stars were the "crucible" in which light elements combined to create heavy elements, but without more accurate measurements of their atomic masses nothing more could be said at the time.
All of these speculations were proven correct in the following decades.
The primary source of solar energy, and that of similar size stars, is the fusion of hydrogen to form helium (the proton–proton chain reaction), which occurs at a solar-core temperature of 14 million kelvin. The net result is the fusion of four protons into one alpha particle, with the release of two positrons and two neutrinos (which changes two of the protons into neutrons), and energy. In heavier stars, the CNO cycle and other processes are more important. As a star uses up a substantial fraction of its hydrogen, it begins to fuse heavier elements. In massive cores, silicon-burning is the final fusion cycle, leading to a build-up of iron and nickel nuclei.
Nuclear binding energy makes the production of elements heavier than nickel via fusion energetically unfavorable. These elements are produced in non-fusion processes: the s-process, r-process, and the variety of processes that can produce p-nuclei. Such processes occur in giant star shells, or supernovae, or neutron star mergers.
Brown dwarfs
Brown dwarfs fuse deuterium and in very high mass cases also fuse lithium.
White dwarfs
Carbon-oxygen white dwarfs, which accrete matter either from an active stellar companion or white dwarf merger, approach the Chandrasekhar limit of 1.44 solar masses. Immediately prior, carbon burning fusion begins, destroying the Earth-sized dwarf within one second, in a Type Ia supernova.
Much more rarely, helium white dwarfs may merge, which does not cause an explosion but begins helium burning in an extreme type of helium star.
Neutron stars
Some neutron stars accrete hydrogen and helium from an active stellar companion. Periodically, the helium accretion reaches a critical level, and a thermonuclear burn wave propagates across the surface, on the timescale of one second.[29]
Black hole accretion disks
Similar to stellar fusion, extreme conditions within black hole accretion disks can allow fusion reactions. Calculations show the most energetic reactions occur around lower stellar mass black holes, below 10 solar masses, compared to those above 100. Beyond five Schwarzschild radii, carbon-burning and fusion of helium-3 dominates the reactions. Within this distance, around lower mass black holes, fusion of nitrogen, oxygen, neon, and magnesium can occur. In the extreme limit, the silicon-burning process can begin with the fusion of silicon and selenium nuclei.[30]
Big Bang
From the period approximately 10 seconds to 20 minutes after the Big Bang, the universe cooled from over 100 keV to 1 keV. This allowed the combination of protons and neutrons in deuterium nuclei, and beginning a rapid fusion chain into tritium and helium-3 and ending in predominantly helium-4, with a minimal fraction of lithium, beryllium, and boron nuclei.
Requirements
Summarize
Perspective
This article needs additional citations for verification. (October 2024) |

A substantial energy barrier of electrostatic forces must be overcome before fusion can occur. At large distances, two naked nuclei repel one another because of the repulsive electrostatic force between their positively charged protons. If two nuclei can be brought close enough together, however, the electrostatic repulsion can be overcome by the quantum effect in which nuclei can tunnel through coulomb forces.
When a nucleon such as a proton or neutron is added to a nucleus, the nuclear force attracts it to all the other nucleons of the nucleus (if the atom is small enough), but primarily to its immediate neighbors due to the short range of the force. The nucleons in the interior of a nucleus have more neighboring nucleons than those on the surface. Since smaller nuclei have a larger surface-area-to-volume ratio, the binding energy per nucleon due to the nuclear force generally increases with the size of the nucleus but approaches a limiting value corresponding to that of a nucleus with a diameter of about four nucleons. It is important to keep in mind that nucleons are quantum objects. So, for example, since two neutrons in a nucleus are identical to each other, the goal of distinguishing one from the other, such as which one is in the interior and which is on the surface, is in fact meaningless, and the inclusion of quantum mechanics is therefore necessary for proper calculations.
The electrostatic force, on the other hand, is an inverse-square force, so a proton added to a nucleus will feel an electrostatic repulsion from all the other protons in the nucleus. The electrostatic energy per nucleon due to the electrostatic force thus increases without limit as nuclei atomic number grows.

The net result of the opposing electrostatic and strong nuclear forces is that the binding energy per nucleon generally increases with increasing size, up to the elements iron and nickel, and then decreases for heavier nuclei. Eventually, the binding energy becomes negative and very heavy nuclei (all with more than 208 nucleons, corresponding to a diameter of about 6 nucleons) are not stable. The four most tightly bound nuclei, in decreasing order of binding energy per nucleon, are 62
Ni
, 58
Fe
, 56
Fe
, and 60
Ni
.[31] Even though the nickel isotope, 62
Ni
, is more stable, the iron isotope 56
Fe
is an order of magnitude more common. This is due to the fact that there is no easy way for stars to create 62
Ni
through the alpha process.
An exception to this general trend is the helium-4 nucleus, whose binding energy is higher than that of lithium, the next heavier element. This is because protons and neutrons are fermions, which according to the Pauli exclusion principle cannot exist in the same nucleus in exactly the same state. Each proton or neutron's energy state in a nucleus can accommodate both a spin up particle and a spin down particle. Helium-4 has an anomalously large binding energy because its nucleus consists of two protons and two neutrons (it is a doubly magic nucleus), so all four of its nucleons can be in the ground state. Any additional nucleons would have to go into higher energy states. Indeed, the helium-4 nucleus is so tightly bound that it is commonly treated as a single quantum mechanical particle in nuclear physics, namely, the alpha particle.
The situation is similar if two nuclei are brought together. As they approach each other, all the protons in one nucleus repel all the protons in the other. Not until the two nuclei actually come close enough for long enough so the strong attractive nuclear force can take over and overcome the repulsive electrostatic force. This can also be described as the nuclei overcoming the so-called Coulomb barrier. The kinetic energy to achieve this can be lower than the barrier itself because of quantum tunneling.
The Coulomb barrier is smallest for isotopes of hydrogen, as their nuclei contain only a single positive charge. A diproton is not stable, so neutrons must also be involved, ideally in such a way that a helium nucleus, with its extremely tight binding, is one of the products.
Using deuterium–tritium fuel, the resulting energy barrier is about 0.1 MeV. In comparison, the energy needed to remove an electron from hydrogen is 13.6 eV. The (intermediate) result of the fusion is an unstable 5He nucleus, which immediately ejects a neutron with 14.1 MeV. The recoil energy of the remaining 4He nucleus is 3.5 MeV, so the total energy liberated is 17.6 MeV. This is many times more than what was needed to overcome the energy barrier.
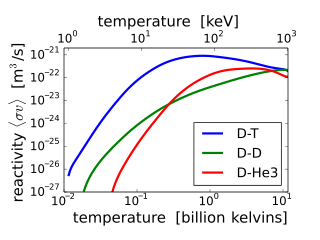
The reaction cross section (σ) is a measure of the probability of a fusion reaction as a function of the relative velocity of the two reactant nuclei. If the reactants have a distribution of velocities, e.g. a thermal distribution, then it is useful to perform an average over the distributions of the product of cross-section and velocity. This average is called the 'reactivity', denoted ⟨σv⟩. The reaction rate (fusions per volume per time) is ⟨σv⟩ times the product of the reactant number densities:
If a species of nuclei is reacting with a nucleus like itself, such as the DD reaction, then the product must be replaced by .
increases from virtually zero at room temperatures up to meaningful magnitudes at temperatures of 10–100 keV. At these temperatures, well above typical ionization energies (13.6 eV in the hydrogen case), the fusion reactants exist in a plasma state.
The significance of as a function of temperature in a device with a particular energy confinement time is found by considering the Lawson criterion. This is an extremely challenging barrier to overcome on Earth, which explains why fusion research has taken many years to reach the current advanced technical state.[32][33]
Artificial fusion
Summarize
Perspective
Thermonuclear fusion
Thermonuclear fusion is the process of atomic nuclei combining or "fusing" using high temperatures to drive them close enough together for this to become possible. Such temperatures cause the matter to become a plasma and, if confined, fusion reactions may occur due to collisions with extreme thermal kinetic energies of the particles. There are two forms of thermonuclear fusion: uncontrolled, in which the resulting energy is released in an uncontrolled manner, as it is in thermonuclear weapons ("hydrogen bombs") and in most stars; and controlled, where the fusion reactions take place in an environment allowing some or all of the energy released to be harnessed for constructive purposes.
Temperature is a measure of the average kinetic energy of particles, so by heating the material it will gain energy. After reaching sufficient temperature, given by the Lawson criterion, the energy of accidental collisions within the plasma is high enough to overcome the Coulomb barrier and the particles may fuse together.
In a deuterium–tritium fusion reaction, for example, the energy necessary to overcome the Coulomb barrier is 0.1 MeV. Converting between energy and temperature shows that the 0.1 MeV barrier would be overcome at a temperature in excess of 1.2 billion kelvin.
There are two effects that are needed to lower the actual temperature. One is the fact that temperature is the average kinetic energy, implying that some nuclei at this temperature would actually have much higher energy than 0.1 MeV, while others would be much lower. It is the nuclei in the high-energy tail of the velocity distribution that account for most of the fusion reactions. The other effect is quantum tunnelling. The nuclei do not actually have to have enough energy to overcome the Coulomb barrier completely. If they have nearly enough energy, they can tunnel through the remaining barrier. For these reasons fuel at lower temperatures will still undergo fusion events, at a lower rate.
Thermonuclear fusion is one of the methods being researched in the attempts to produce fusion power. If thermonuclear fusion becomes favorable to use, it would significantly reduce the world's carbon footprint.
Beam–beam or beam–target fusion
Accelerator-based light-ion fusion is a technique using particle accelerators to achieve particle kinetic energies sufficient to induce light-ion fusion reactions.[34]
Accelerating light ions is relatively easy, and can be done in an efficient manner—requiring only a vacuum tube, a pair of electrodes, and a high-voltage transformer; fusion can be observed with as little as 10 kV between the electrodes.[citation needed] The system can be arranged to accelerate ions into a static fuel-infused target, known as beam–target fusion, or by accelerating two streams of ions towards each other, beam–beam fusion.[citation needed] The key problem with accelerator-based fusion (and with cold targets in general) is that fusion cross sections are many orders of magnitude lower than Coulomb interaction cross-sections. Therefore, the vast majority of ions expend their energy emitting bremsstrahlung radiation and the ionization of atoms of the target. Devices referred to as sealed-tube neutron generators are particularly relevant to this discussion. These small devices are miniature particle accelerators filled with deuterium and tritium gas in an arrangement that allows ions of those nuclei to be accelerated against hydride targets, also containing deuterium and tritium, where fusion takes place, releasing a flux of neutrons. Hundreds of neutron generators are produced annually for use in the petroleum industry where they are used in measurement equipment for locating and mapping oil reserves.[citation needed]
A number of attempts to recirculate the ions that "miss" collisions have been made over the years. One of the better-known attempts in the 1970s was Migma, which used a unique particle storage ring to capture ions into circular orbits and return them to the reaction area. Theoretical calculations made during funding reviews pointed out that the system would have significant difficulty scaling up to contain enough fusion fuel to be relevant as a power source. In the 1990s, a new arrangement using a field-reversed configuration (FRC) as the storage system was proposed by Norman Rostoker and continues to be studied by TAE Technologies as of 2021[update]. A closely related approach is to merge two FRC's rotating in opposite directions,[35] which is being actively studied by Helion Energy. Because these approaches all have ion energies well beyond the Coulomb barrier, they often suggest the use of alternative fuel cycles like p-11B that are too difficult to attempt using conventional approaches.[36]
Element synthesis
Fusion of very heavy target nuclei with accelerated ion beams is the primary method of element synthesis. In early 1930s nuclear experiments, deuteron beams were used, to discover the first synthetic elements, such as technetium, neptunium, and plutonium:
Fusion of very heavy target nuclei with heavy ion beams has been used to discover superheavy elements:
Muon-catalyzed fusion
Muon-catalyzed fusion is a fusion process that occurs at ordinary temperatures. It was studied in detail by Steven Jones in the early 1980s. Net energy production from this reaction has been unsuccessful because of the high energy required to create muons, their short 2.2 μs half-life, and the high chance that a muon will bind to the new alpha particle and thus stop catalyzing fusion.[37]
Other principles

Some other confinement principles have been investigated.
- Antimatter-initialized fusion uses small amounts of antimatter to trigger a tiny fusion explosion. This has been studied primarily in the context of making nuclear pulse propulsion, and pure fusion bombs feasible. This is not near becoming a practical power source, due to the cost of manufacturing antimatter alone.
- Pyroelectric fusion was reported in April 2005 by a team at UCLA. The scientists used a pyroelectric crystal heated from −34 to 7 °C (−29 to 45 °F), combined with a tungsten needle to produce an electric field of about 25 gigavolts per meter to ionize and accelerate deuterium nuclei into an erbium deuteride target. At the estimated energy levels,[38] the D–D fusion reaction may occur, producing helium-3 and a 2.45 MeV neutron. Although it makes a useful neutron generator, the apparatus is not intended for power generation since it requires far more energy than it produces.[39][40][41][42] D–T fusion reactions have been observed with a tritiated erbium target.[43]
- Nuclear fusion–fission hybrid (hybrid nuclear power) is a proposed means of generating power by use of a combination of nuclear fusion and fission processes. The concept dates to the 1950s, and was briefly advocated by Hans Bethe during the 1970s, but largely remained unexplored until a revival of interest in 2009, due to the delays in the realization of pure fusion.[44]
- Project PACER, carried out at Los Alamos National Laboratory (LANL) in the mid-1970s, explored the possibility of a fusion power system that would involve exploding small hydrogen bombs (fusion bombs) inside an underground cavity. As an energy source, the system is the only fusion power system that could be demonstrated to work using existing technology. However, it would also require a large, continuous supply of nuclear bombs, making the economics of such a system rather questionable.
- Bubble fusion also called sonofusion was a proposed mechanism for achieving fusion via sonic cavitation which rose to prominence in the early 2000s. Subsequent attempts at replication failed and the principal investigator, Rusi Taleyarkhan, was judged guilty of research misconduct in 2008.[45]
Confinement in thermonuclear fusion
Summarize
Perspective
The key problem in achieving thermonuclear fusion is how to confine the hot plasma. Due to the high temperature, the plasma cannot be in direct contact with any solid material, so it has to be located in a vacuum. Also, high temperatures imply high pressures. The plasma tends to expand immediately and some force is necessary to act against it. This force can take one of three forms: gravitation in stars, magnetic forces in magnetic confinement fusion reactors, or inertial as the fusion reaction may occur before the plasma starts to expand, so the plasma's inertia is keeping the material together.
Gravitational confinement
One force capable of confining the fuel well enough to satisfy the Lawson criterion is gravity. The mass needed, however, is so great that gravitational confinement is only found in stars—the least massive stars capable of sustained fusion are red dwarfs, while brown dwarfs are able to fuse deuterium and lithium if they are of sufficient mass. In stars heavy enough, after the supply of hydrogen is exhausted in their cores, their cores (or a shell around the core) start fusing helium to carbon. In the most massive stars (at least 8–11 solar masses), the process is continued until some of their energy is produced by fusing lighter elements to iron. As iron has one of the highest binding energies, reactions producing heavier elements are generally endothermic. Therefore, significant amounts of heavier elements are not formed during stable periods of massive star evolution, but are formed in supernova explosions. Some lighter stars also form these elements in the outer parts of the stars over long periods of time, by absorbing energy from fusion in the inside of the star, by absorbing neutrons that are emitted from the fusion process.
All of the elements heavier than iron have some potential energy to release, in theory. At the extremely heavy end of element production, these heavier elements can produce energy in the process of being split again back toward the size of iron, in the process of nuclear fission. Nuclear fission thus releases energy that has been stored, sometimes billions of years before, during stellar nucleosynthesis.
Magnetic confinement
Electrically charged particles (such as fuel ions) will follow magnetic field lines (see Guiding centre). The fusion fuel can therefore be trapped using a strong magnetic field. A variety of magnetic configurations exist, including the toroidal geometries of tokamaks and stellarators and open-ended mirror confinement systems.
Inertial confinement
A third confinement principle is to apply a rapid pulse of energy to a large part of the surface of a pellet of fusion fuel, causing it to simultaneously "implode" and heat to very high pressure and temperature. If the fuel is dense enough and hot enough, the fusion reaction rate will be high enough to burn a significant fraction of the fuel before it has dissipated. To achieve these extreme conditions, the initially cold fuel must be explosively compressed. Inertial confinement is used in the hydrogen bomb, where the driver is x-rays created by a fission bomb. Inertial confinement is also attempted in "controlled" nuclear fusion, where the driver is a laser, ion, or electron beam, or a Z-pinch. Another method is to use conventional high explosive material to compress a fuel to fusion conditions.[46][47] The UTIAS explosive-driven-implosion facility was used to produce stable, centred and focused hemispherical implosions[48] to generate neutrons from D-D reactions. The simplest and most direct method proved to be in a predetonated stoichiometric mixture of deuterium-oxygen. The other successful method was using a miniature Voitenko compressor,[49] where a plane diaphragm was driven by the implosion wave into a secondary small spherical cavity that contained pure deuterium gas at one atmosphere.[50]
Electrostatic confinement
There are also electrostatic confinement fusion devices. These devices confine ions using electrostatic fields. The best known is the fusor. This device has a cathode inside an anode wire cage. Positive ions fly towards the negative inner cage, and are heated by the electric field in the process. If they miss the inner cage they can collide and fuse. Ions typically hit the cathode, however, creating prohibitory high conduction losses. Also, fusion rates in fusors are very low due to competing physical effects, such as energy loss in the form of light radiation.[51] Designs have been proposed to avoid the problems associated with the cage, by generating the field using a non-neutral cloud. These include a plasma oscillating device,[52] a Penning trap and the polywell.[53] The technology is relatively immature, however, and many scientific and engineering questions remain.
The most well known Inertial electrostatic confinement approach is the fusor. Starting in 1999, a number of amateurs have been able to do amateur fusion using these homemade devices.[54][55][56][57] Other IEC devices include: the Polywell, MIX POPS[58] and Marble concepts.[59]
Important reactions
Summarize
Perspective
Stellar reaction chains
At the temperatures and densities in stellar cores, the rates of fusion reactions are notoriously slow. For example, at solar core temperature (T ≈ 15 MK) and density (160 g/cm3), the energy release rate is only 276 μW/cm3—about a quarter of the volumetric rate at which a resting human body generates heat.[60] Thus, reproduction of stellar core conditions in a lab for nuclear fusion power production is completely impractical. Because nuclear reaction rates depend on density as well as temperature, and most fusion schemes operate at relatively low densities, those methods are strongly dependent on higher temperatures. The fusion rate as a function of temperature (exp(−E/kT)), leads to the need to achieve temperatures in terrestrial reactors 10–100 times higher than in stellar interiors: T ≈ (0.1–1.0)×109 K.
Criteria and candidates for terrestrial reactions
In artificial fusion, the primary fuel is not constrained to be protons and higher temperatures can be used, so reactions with larger cross-sections are chosen. Another concern is the production of neutrons, which activate the reactor structure radiologically, but also have the advantages of allowing volumetric extraction of the fusion energy and tritium breeding. Reactions that release no neutrons are referred to as aneutronic.
To be a useful energy source, a fusion reaction must satisfy several criteria. It must:
- Be exothermic
- This limits the reactants to the low Z (number of protons) side of the curve of binding energy. It also makes helium 4
He
the most common product because of its extraordinarily tight binding, although 3
He
and 3
H
also show up. - Involve low atomic number (Z) nuclei
- This is because the electrostatic repulsion that must be overcome before the nuclei are close enough to fuse ( Coulomb barrier ) is directly related to the number of protons it contains – its atomic number.
- Have two reactants
- At anything less than stellar densities, three-body collisions are too improbable. In inertial confinement, both stellar densities and temperatures are exceeded to compensate for the shortcomings of the third parameter of the Lawson criterion, ICF's very short confinement time.
- Have two or more products
- This allows simultaneous conservation of energy and momentum without relying on the electromagnetic force.
- Conserve both protons and neutrons
- The cross sections for the weak interaction are too small.
Few reactions meet these criteria. The following are those with the largest cross sections:[61][62]
(1) 2
1D
+ 3
1T
→ 4
2He
( 3.52 MeV ) + n0 ( 14.06 MeV ) (2i) 2
1D
+ 2
1D
→ 3
1T
( 1.01 MeV ) + p+ ( 3.02 MeV ) 50% (2ii) → 3
2He
( 0.82 MeV ) + n0 ( 2.45 MeV ) 50% (3) 2
1D
+ 3
2He
→ 4
2He
( 3.6 MeV ) + p+ ( 14.7 MeV ) (4) 3
1T
+ 3
1T
→ 4
2He
+ 2 n0 + 11.3 MeV (5) 3
2He
+ 3
2He
→ 4
2He
+ 2 p+ + 12.9 MeV (6i) 3
2He
+ 3
1T
→ 4
2He
+ p+ + n0 + 12.1 MeV 57% (6ii) → 4
2He
( 4.8 MeV ) + 2
1D
( 9.5 MeV ) 43% (7i) 2
1D
+ 6
3Li
→ 2 4
2He
+ 22.4 MeV (7ii) → 3
2He
+ 4
2He
+ n0 + 2.56 MeV (7iii) → 7
3Li
+ p+ + 5.0 MeV (7iv) → 7
4Be
+ n0 + 3.4 MeV (8) p+ + 6
3Li
→ 4
2He
( 1.7 MeV ) + 3
2He
( 2.3 MeV ) (9) 3
2He
+ 6
3Li
→ 2 4
2He
+ p+ + 16.9 MeV (10) p+ + 11
5B
→ 3 4
2He
+ 8.7 MeV
For reactions with two products, the energy is divided between them in inverse proportion to their masses, as shown. In most reactions with three products, the distribution of energy varies. For reactions that can result in more than one set of products, the branching ratios are given.
Some reaction candidates can be eliminated at once. The D–6Li reaction has no advantage compared to p+–11
5B
because it is roughly as difficult to burn but produces substantially more neutrons through 2
1D
–2
1D
side reactions. There is also a p+–7
3Li
reaction, but the cross section is far too low, except possibly when Ti > 1 MeV, but at such high temperatures an endothermic, direct neutron-producing reaction also becomes very significant. Finally there is also a p+–9
4Be
reaction, which is not only difficult to burn, but 9
4Be
can be easily induced to split into two alpha particles and a neutron.
In addition to the fusion reactions, the following reactions with neutrons are important in order to "breed" tritium in "dry" fusion bombs and some proposed fusion reactors:
The latter of the two equations was unknown when the U.S. conducted the Castle Bravo fusion bomb test in 1954. Being just the second fusion bomb ever tested (and the first to use lithium), the designers of the Castle Bravo "Shrimp" had understood the usefulness of 6Li in tritium production, but had failed to recognize that 7Li fission would greatly increase the yield of the bomb. While 7Li has a small neutron cross-section for low neutron energies, it has a higher cross section above 5 MeV.[63] The 15 Mt yield was 150% greater than the predicted 6 Mt and caused unexpected exposure to fallout.
To evaluate the usefulness of these reactions, in addition to the reactants, the products, and the energy released, one needs to know something about the nuclear cross section. Any given fusion device has a maximum plasma pressure it can sustain, and an economical device would always operate near this maximum. Given this pressure, the largest fusion output is obtained when the temperature is chosen so that ⟨σv⟩/T2 is a maximum. This is also the temperature at which the value of the triple product nTτ required for ignition is a minimum, since that required value is inversely proportional to ⟨σv⟩/T2 (see Lawson criterion). (A plasma is "ignited" if the fusion reactions produce enough power to maintain the temperature without external heating.) This optimum temperature and the value of ⟨σv⟩/T2 at that temperature is given for a few of these reactions in the following table.
| fuel | T [keV] | ⟨σv⟩/T2 [m3/s/keV2] |
|---|---|---|
| 2 1D –3 1T | 13.6 | 1.24×10−24 |
| 2 1D –2 1D | 15 | 1.28×10−26 |
| 2 1D –3 2He | 58 | 2.24×10−26 |
| p+–6 3Li | 66 | 1.46×10−27 |
| p+–11 5B | 123 | 3.01×10−27 |
Note that many of the reactions form chains. For instance, a reactor fueled with 3
1T
and 3
2He
creates some 2
1D
, which is then possible to use in the 2
1D
–3
2He
reaction if the energies are "right". An elegant idea is to combine the reactions (8) and (9). The 3
2He
from reaction (8) can react with 6
3Li
in reaction (9) before completely thermalizing. This produces an energetic proton, which in turn undergoes reaction (8) before thermalizing. Detailed analysis shows that this idea would not work well,[citation needed] but it is a good example of a case where the usual assumption of a Maxwellian plasma is not appropriate.
Abundance of the nuclear fusion fuels
| Nuclear Fusion Fuel Isotope | Half-Life | Abundance |
|---|---|---|
| 1 1H [64][65][66][67][68][69][70][71][excessive citations] |
Stable | 99.98% |
| 2 1D [72][73][74][75] |
Stable | 0.02% |
| 3 1T [72][73] |
12.32(2) y | trace |
| 3 2He [72][73][74] |
stable | 0.0002% |
| 4 2He [75] |
stable | 99.9998% |
| 6 3Li [72][73][74] |
stable | 7.59% |
| 7 3Li [72][74] |
stable | 92.41% |
| 11 5B [72][73][74][76] |
stable | 80% |
| 12 6C [65][69] |
stable | 98.9% |
| 13 6C [65] |
stable | 1.1% |
| 13 7N [65][69] |
9.965(4) min | syn |
| 14 7N [65][66][69] |
stable | 99.6% |
| 15 7N [65][66][67][69][70][74][excessive citations] |
stable | 0.4% |
| 14 8O [69] |
70.621(11) s | syn |
| 15 8O [65][66][69][70] |
122.266(43) s | syn |
| 16 8O [66][67][68][70][71][excessive citations] |
stable | 99.76% |
| 17 8O [66][67][68] |
stable | 0.04% |
| 18 8O [67][68] |
stable | 0.20% |
| 17 9F [66][67][68][70][71] |
64.370(27) s | syn |
| 18 9F [67][68][70][71] |
109.734(8) min | trace |
| 19 9F [68][71] |
stable | 100% |
| 18 10Ne [70][71] |
1664.20(47) ms | trace |
| 19 10Ne [71] |
17.2569(19) s | trace |
Neutronicity, confinement requirement, and power density
Any of the reactions above can in principle be the basis of fusion power production. In addition to the temperature and cross section discussed above, we must consider the total energy of the fusion products Efus, the energy of the charged fusion products Ech, and the atomic number Z of the non-hydrogenic reactant.
Specification of the 2
1D
–2
1D
reaction entails some difficulties, though. To begin with, one must average over the two branches (2i) and (2ii). More difficult is to decide how to treat the 3
1T
and 3
2He
products. 3
1T
burns so well in a deuterium plasma that it is almost impossible to extract from the plasma. The 2
1D
–3
2He
reaction is optimized at a much higher temperature, so the burnup at the optimum 2
1D
–2
1D
temperature may be low. Therefore, it seems reasonable to assume the 3
1T
but not the 3
2He
gets burned up and adds its energy to the net reaction, which means the total reaction would be the sum of (2i), (2ii), and (1):
- 5 2
1D
→ 4
2He
+ 2 n0 + 3
2He
+ p+, Efus = 4.03 + 17.6 + 3.27 = 24.9 MeV, Ech = 4.03 + 3.5 + 0.82 = 8.35 MeV.
For calculating the power of a reactor (in which the reaction rate is determined by the D–D step), we count the 2
1D
–2
1D
fusion energy per D–D reaction as Efus = (4.03 MeV + 17.6 MeV) × 50% + (3.27 MeV) × 50% = 12.5 MeV and the energy in charged particles as Ech = (4.03 MeV + 3.5 MeV) × 50% + (0.82 MeV) × 50% = 4.2 MeV. (Note: if the tritium ion reacts with a deuteron while it still has a large kinetic energy, then the kinetic energy of the helium-4 produced may be quite different from 3.5 MeV,[77] so this calculation of energy in charged particles is only an approximation of the average.) The amount of energy per deuteron consumed is 2/5 of this, or 5.0 MeV (a specific energy of about 225 million MJ per kilogram of deuterium).
Another unique aspect of the 2
1D
–2
1D
reaction is that there is only one reactant, which must be taken into account when calculating the reaction rate.
With this choice, we tabulate parameters for four of the most important reactions
| fuel | Z | Efus [MeV] | Ech [MeV] | neutronicity |
|---|---|---|---|---|
| 2 1D –3 1T | 1 | 17.6 | 3.5 | 0.80 |
| 2 1D –2 1D | 1 | 12.5 | 4.2 | 0.66 |
| 2 1D –3 2He | 2 | 18.3 | 18.3 | ≈0.05 |
| p+–11 5B | 5 | 8.7 | 8.7 | ≈0.001 |
The last column is the neutronicity of the reaction, the fraction of the fusion energy released as neutrons. This is an important indicator of the magnitude of the problems associated with neutrons like radiation damage, biological shielding, remote handling, and safety. For the first two reactions it is calculated as (Efus − Ech)/Efus. For the last two reactions, where this calculation would give zero, the values quoted are rough estimates based on side reactions that produce neutrons in a plasma in thermal equilibrium.
Of course, the reactants should also be mixed in the optimal proportions. This is the case when each reactant ion plus its associated electrons accounts for half the pressure. Assuming that the total pressure is fixed, this means that particle density of the non-hydrogenic ion is smaller than that of the hydrogenic ion by a factor 2/(Z + 1). Therefore, the rate for these reactions is reduced by the same factor, on top of any differences in the values of ⟨σv⟩/T2. On the other hand, because the 2
1D
–2
1D
reaction has only one reactant, its rate is twice as high as when the fuel is divided between two different hydrogenic species, thus creating a more efficient reaction.
Thus there is a "penalty" of 2/(Z + 1) for non-hydrogenic fuels arising from the fact that they require more electrons, which take up pressure without participating in the fusion reaction. (It is usually a good assumption that the electron temperature will be nearly equal to the ion temperature. Some authors, however, discuss the possibility that the electrons could be maintained substantially colder than the ions. In such a case, known as a "hot ion mode", the "penalty" would not apply.) There is at the same time a "bonus" of a factor 2 for 2
1D
–2
1D
because each ion can react with any of the other ions, not just a fraction of them.
We can now compare these reactions in the following table.
| fuel | ⟨σv⟩/T2 | penalty/bonus | inverse reactivity | Lawson criterion | power density [W/m3/kPa2] | inverse ratio of power density |
|---|---|---|---|---|---|---|
| 2 1D –3 1T | 1.24×10−24 | 1 | 1 | 1 | 34 | 1 |
| 2 1D –2 1D | 1.28×10−26 | 2 | 48 | 30 | 0.5 | 68 |
| 2 1D –3 2He | 2.24×10−26 | 2/3 | 83 | 16 | 0.43 | 80 |
| p+–6 3Li | 1.46×10−27 | 1/2 | 1700 | 0.005 | 6800 | |
| p+–11 5B | 3.01×10−27 | 1/3 | 1240 | 500 | 0.014 | 2500 |
The maximum value of ⟨σv⟩/T2 is taken from a previous table. The "penalty/bonus" factor is that related to a non-hydrogenic reactant or a single-species reaction. The values in the column "inverse reactivity" are found by dividing 1.24×10−24 by the product of the second and third columns. It indicates the factor by which the other reactions occur more slowly than the 2
1D
–3
1T
reaction under comparable conditions. The column "Lawson criterion" weights these results with Ech and gives an indication of how much more difficult it is to achieve ignition with these reactions, relative to the difficulty for the 2
1D
–3
1T
reaction. The next-to-last column is labeled "power density" and weights the practical reactivity by Efus. The final column indicates how much lower the fusion power density of the other reactions is compared to the 2
1D
–3
1T
reaction and can be considered a measure of the economic potential.
Bremsstrahlung losses in quasineutral, isotropic plasmas
The ions undergoing fusion in many systems will essentially never occur alone but will be mixed with electrons that in aggregate neutralize the ions' bulk electrical charge and form a plasma. The electrons will generally have a temperature comparable to or greater than that of the ions, so they will collide with the ions and emit x-ray radiation of 10–30 keV energy, a process known as Bremsstrahlung.
The huge size of the Sun and stars means that the x-rays produced in this process will not escape and will deposit their energy back into the plasma. They are said to be opaque to x-rays. But any terrestrial fusion reactor will be optically thin for x-rays of this energy range. X-rays are difficult to reflect but they are effectively absorbed (and converted into heat) in less than mm thickness of stainless steel (which is part of a reactor's shield). This means the bremsstrahlung process is carrying energy out of the plasma, cooling it.
The ratio of fusion power produced to x-ray radiation lost to walls is an important figure of merit. This ratio is generally maximized at a much higher temperature than that which maximizes the power density (see the previous subsection). The following table shows estimates of the optimum temperature and the power ratio at that temperature for several reactions:
| fuel | Ti [keV] | Pfusion/PBremsstrahlung |
|---|---|---|
| 2 1D –3 1T | 50 | 140 |
| 2 1D –2 1D | 500 | 2.9 |
| 2 1D –3 2He | 100 | 5.3 |
| 3 2He –3 2He | 1000 | 0.72 |
| p+–6 3Li | 800 | 0.21 |
| p+–11 5B | 300 | 0.57 |
The actual ratios of fusion to Bremsstrahlung power will likely be significantly lower for several reasons. For one, the calculation assumes that the energy of the fusion products is transmitted completely to the fuel ions, which then lose energy to the electrons by collisions, which in turn lose energy by Bremsstrahlung. However, because the fusion products move much faster than the fuel ions, they will give up a significant fraction of their energy directly to the electrons. Secondly, the ions in the plasma are assumed to be purely fuel ions. In practice, there will be a significant proportion of impurity ions, which will then lower the ratio. In particular, the fusion products themselves must remain in the plasma until they have given up their energy, and will remain for some time after that in any proposed confinement scheme. Finally, all channels of energy loss other than Bremsstrahlung have been neglected. The last two factors are related. On theoretical and experimental grounds, particle and energy confinement seem to be closely related. In a confinement scheme that does a good job of retaining energy, fusion products will build up. If the fusion products are efficiently ejected, then energy confinement will be poor, too.
The temperatures maximizing the fusion power compared to the Bremsstrahlung are in every case higher than the temperature that maximizes the power density and minimizes the required value of the fusion triple product. This will not change the optimum operating point for 2
1D
–3
1T
very much because the Bremsstrahlung fraction is low, but it will push the other fuels into regimes where the power density relative to 2
1D
–3
1T
is even lower and the required confinement even more difficult to achieve. For 2
1D
–2
1D
and 2
1D
–3
2He
, Bremsstrahlung losses will be a serious, possibly prohibitive problem. For 3
2He
–3
2He
, p+–6
3Li
and p+–11
5B
the Bremsstrahlung losses appear to make a fusion reactor using these fuels with a quasineutral, isotropic plasma impossible. Some ways out of this dilemma have been considered but rejected.[78][79] This limitation does not apply to non-neutral and anisotropic plasmas; however, these have their own challenges to contend with.
Mathematical description of cross section
Summarize
Perspective
Fusion under classical physics
In a classical picture, nuclei can be understood as hard spheres that repel each other through the Coulomb force but fuse once the two spheres come close enough for contact. Estimating the radius of an atomic nuclei as about one femtometer, the energy needed for fusion of two hydrogen is:
This would imply that for the core of the sun, which has a Boltzmann distribution with a temperature of around 1.4 keV, the probability hydrogen would reach the threshold is , that is, fusion would never occur. However, fusion in the sun does occur due to quantum mechanics.
Parameterization of cross section
The probability that fusion occurs is greatly increased compared to the classical picture, thanks to the smearing of the effective radius as the de Broglie wavelength as well as quantum tunneling through the potential barrier. To determine the rate of fusion reactions, the value of most interest is the cross section, which describes the probability that particles will fuse by giving a characteristic area of interaction. An estimation of the fusion cross-sectional area is often broken into three pieces:
where is the geometric cross section, T is the barrier transparency and R is the reaction characteristics of the reaction.
is of the order of the square of the de Broglie wavelength where is the reduced mass of the system and is the center of mass energy of the system.
T can be approximated by the Gamow transparency, which has the form: where is the Gamow factor and comes from estimating the quantum tunneling probability through the potential barrier.
R contains all the nuclear physics of the specific reaction and takes very different values depending on the nature of the interaction. However, for most reactions, the variation of is small compared to the variation from the Gamow factor and so is approximated by a function called the astrophysical S-factor, , which is weakly varying in energy. Putting these dependencies together, one approximation for the fusion cross section as a function of energy takes the form:
More detailed forms of the cross-section can be derived through nuclear physics-based models and R-matrix theory.
Formulas of fusion cross sections
The Naval Research Lab's plasma physics formulary[80] gives the total cross section in barns as a function of the energy (in keV) of the incident particle towards a target ion at rest fit by the formula:
- with the following coefficient values:
| DT(1) | DD(2i) | DD(2ii) | DHe3(3) | TT(4) | The3(6) | |
|---|---|---|---|---|---|---|
| A1 | 45.95 | 46.097 | 47.88 | 89.27 | 38.39 | 123.1 |
| A2 | 50200 | 372 | 482 | 25900 | 448 | 11250 |
| A3 | 1.368×10−2 | 4.36×10−4 | 3.08×10−4 | 3.98×10−3 | 1.02×10−3 | 0 |
| A4 | 1.076 | 1.22 | 1.177 | 1.297 | 2.09 | 0 |
| A5 | 409 | 0 | 0 | 647 | 0 | 0 |
Bosch-Hale[81] also reports a R-matrix calculated cross sections fitting observation data with Padé rational approximating coefficients. With energy in units of keV and cross sections in units of millibarn, the factor has the form:
- , with the coefficient values:
| DT(1) | DD(2ii) | DHe3(3) | The4 | |
|---|---|---|---|---|
| 31.3970 | 68.7508 | 31.3970 | 34.3827 | |
| A1 | 5.5576×104 | 5.7501×106 | 5.3701×104 | 6.927×104 |
| A2 | 2.1054×102 | 2.5226×103 | 3.3027×102 | 7.454×108 |
| A3 | −3.2638×10−2 | 4.5566×101 | −1.2706×10−1 | 2.050×106 |
| A4 | 1.4987×10−6 | 0 | 2.9327×10−5 | 5.2002×104 |
| A5 | 1.8181×10−10 | 0 | −2.5151×10−9 | 0 |
| B1 | 0 | −3.1995×10−3 | 0 | 6.38×101 |
| B2 | 0 | −8.5530×10−6 | 0 | −9.95×10−1 |
| B3 | 0 | 5.9014×10−8 | 0 | 6.981×10−5 |
| B4 | 0 | 0 | 0 | 1.728×10−4 |
| Applicable Energy Range [keV] | 0.5–5000 | 0.3–900 | 0.5–4900 | 0.5–550 |
| 2.0 | 2.2 | 2.5 | 1.9 |
where
Maxwell-averaged nuclear cross sections
In fusion systems that are in thermal equilibrium, the particles are in a Maxwell–Boltzmann distribution, meaning the particles have a range of energies centered around the plasma temperature. The sun, magnetically confined plasmas and inertial confinement fusion systems are well modeled to be in thermal equilibrium. In these cases, the value of interest is the fusion cross-section averaged across the Maxwell–Boltzmann distribution. The Naval Research Lab's plasma physics formulary tabulates Maxwell averaged fusion cross sections reactivities in .
| Temperature [keV] | DT(1) | DD(2ii) | DHe3(3) | TT(4) | The3(6) |
|---|---|---|---|---|---|
| 1 | 5.5×10−21 | 1.5×10−22 | 1.0×10−26 | 3.3×10−22 | 1.0×10−28 |
| 2 | 2.6×10−19 | 5.4×10−21 | 1.4×10−23 | 7.1×10−21 | 1.0×10−25 |
| 5 | 1.3×10−17 | 1.8×10−19 | 6.7×10−21 | 1.4×10−19 | 2.1×10−22 |
| 10 | 1.1×10−16 | 1.2×10−18 | 2.3×10−19 | 7.2×10−19 | 1.2×10−20 |
| 20 | 4.2×10−16 | 5.2×10−18 | 3.8×10−18 | 2.5×10−18 | 2.6×10−19 |
| 50 | 8.7×10−16 | 2.1×10−17 | 5.4×10−17 | 8.7×10−18 | 5.3×10−18 |
| 100 | 8.5×10−16 | 4.5×10−17 | 1.6×10−16 | 1.9×10−17 | 2.7×10−17 |
| 200 | 6.3×10−16 | 8.8×10−17 | 2.4×10−16 | 4.2×10−17 | 9.2×10−17 |
| 500 | 3.7×10−16 | 1.8×10−16 | 2.3×10−16 | 8.4×10−17 | 2.9×10−16 |
| 1000 | 2.7×10−16 | 2.2×10−16 | 1.8×10−16 | 8.0×10−17 | 5.2×10−16 |
For energies the data can be represented by:
with T in units of keV.
See also
- China Fusion Engineering Test Reactor
- Cold fusion
- Focus fusion
- FuseNet
- Fusion rocket
- Impulse generator
- Joint European Torus
- List of fusion experiments
- List of Fusor examples
- Neutron source
- Nuclear energy
- Nuclear physics
- Nuclear reactor
- Periodic table
- Pulsed power
- Pure fusion weapon
- Teller–Ulam design
- Timeline of nuclear fusion
- Triple-alpha process
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.















![{\displaystyle E_{\ce {thresh}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {Z_{1}Z_{2}}{r}}{\ce {->[{\text{2 protons}}]}}{\frac {1}{4\pi \epsilon _{0}}}{\frac {e^{2}}{1\ {\ce {fm}}}}\approx 1.4\ {\ce {MeV}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ca1291445cce7787dc6d8b4cdf069e51ab63d0dd)













 ,
,  ...
...



