Rectified 5-cubes

In five-dimensional geometry, a rectified 5-cube is a convex uniform 5-polytope, being a rectification of the regular 5-cube.

5-cube	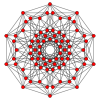Rectified 5-cube	Birectified 5-cube Birectified 5-orthoplex
5-orthoplex	Rectified 5-orthoplex
Orthogonal projections in A5 Coxeter plane

There are 5 degrees of rectifications of a 5-polytope, the zeroth here being the 5-cube, and the 4th and last being the 5-orthoplex. Vertices of the rectified 5-cube are located at the edge-centers of the 5-cube. Vertices of the birectified 5-cube are located in the square face centers of the 5-cube.

Rectified 5-cube

Rectified 5-cube rectified penteract (rin)
Type	uniform 5-polytope
Schläfli symbol	r{4,3,3,3}
Coxeter diagram	=
4-faces	42	10 32
Cells	200	40 160
Faces	400	80 320
Edges	320
Vertices	80
Vertex figure	Tetrahedral prism
Coxeter group	B5, [4,33], order 3840
Dual
Base point	(0,1,1,1,1,1)√2
Circumradius	sqrt(2) = 1.414214
Properties	convex, isogonal

Alternate names

• Rectified penteract (acronym: rin) (Jonathan Bowers)

Construction

The rectified 5-cube may be constructed from the 5-cube by truncating its vertices at the midpoints of its edges.

Coordinates

The Cartesian coordinates of the vertices of the rectified 5-cube with edge length ${\displaystyle {\sqrt {2}}}$ is given by all permutations of:

${\displaystyle (0,\ \pm 1,\ \pm 1,\ \pm 1,\ \pm 1)}$

Images

orthographic projections

Coxeter plane	B5	B4 / D5	B3 / D4 / A2
Graph
Dihedral symmetry	[10]	[8]	[6]
Coxeter plane	B2	A3
Graph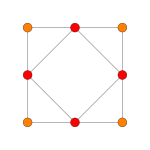
Dihedral symmetry	[4]	[4]

Birectified 5-cube

Birectified 5-cube birectified penteract (nit)
Type	uniform 5-polytope
Schläfli symbol	2r{4,3,3,3}
Coxeter diagram	=
4-faces	42	10 32
Cells	280	40 160 80
Faces	640	320 320
Edges	480
Vertices	80
Vertex figure	{3}×{4}
Coxeter group	B5, [4,33], order 3840 D5, [32,1,1], order 1920
Dual
Base point	(0,0,1,1,1,1)√2
Circumradius	sqrt(3/2) = 1.224745
Properties	convex, isogonal

E. L. Elte identified it in 1912 as a semiregular polytope, identifying it as Cr₅² as a second rectification of a 5-dimensional cross polytope.

Alternate names

• Birectified 5-cube/penteract
• Birectified pentacross/5-orthoplex/triacontiditeron
• Penteractitriacontiditeron (acronym: nit) (Jonathan Bowers)
• Rectified 5-demicube/demipenteract

Construction and coordinates

The birectified 5-cube may be constructed by birectifying the vertices of the 5-cube at ${\displaystyle {\sqrt {2}}}$ of the edge length.

The Cartesian coordinates of the vertices of a birectified 5-cube having edge length 2 are all permutations of:

${\displaystyle \left(0,\ 0,\ \pm 1,\ \pm 1,\ \pm 1\right)}$

Images

orthographic projections

Coxeter plane	B5	B4 / D5	B3 / D4 / A2
Graph
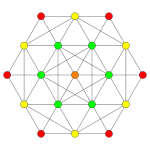Dihedral symmetry	[10]	[8]	[6]
Coxeter plane	B2	A3
Graph
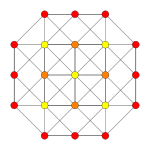Dihedral symmetry	[4]	[4]

Related polytopes

2-isotopic hypercubes

Dim.	2	3	4	5	6	7	8	n
Name	t{4}	r{4,3}	2t{4,3,3}	2r{4,3,3,3}	3t{4,3,3,3,3}	3r{4,3,3,3,3,3}	4t{4,3,3,3,3,3,3}	...
Coxeter diagram
Images
Facets		{3} {4}	t{3,3} t{3,4}	r{3,3,3} r{3,3,4}	2t{3,3,3,3} 2t{3,3,3,4}	2r{3,3,3,3,3} 2r{3,3,3,3,4}	3t{3,3,3,3,3,3} 3t{3,3,3,3,3,4}
Vertex figure	( )v( )	{ }×{ }	{ }v{ }	{3}×{4}	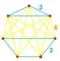{3}v{4}	{3,3}×{3,4}	{3,3}v{3,4}

Related polytopes

These polytopes are a part of 31 uniform polytera generated from the regular 5-cube or 5-orthoplex.

B5 polytopes
β5	t1β5	t2γ5	t1γ5	γ5	t0,1β5	t0,2β5	t1,2β5
t0,3β5	t1,3γ5	t1,2γ5	t0,4γ5	t0,3γ5	t0,2γ5	t0,1γ5	t0,1,2β5
t0,1,3β5	t0,2,3β5	t1,2,3γ5	t0,1,4β5	t0,2,4γ5	t0,2,3γ5	t0,1,4γ5	t0,1,3γ5
t0,1,2γ5	t0,1,2,3β5	t0,1,2,4β5	t0,1,3,4γ5	t0,1,2,4γ5	t0,1,2,3γ5	t0,1,2,3,4γ5

Notes

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "5D uniform polytopes (polytera)". o3x3o3o4o - rin, o3o3x3o4o - nit

External links

• Polytopes of Various Dimensions
• Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds