Pentellated 7-cubes

In seven-dimensional geometry, a pentellated 7-cube is a convex uniform 7-polytope with 5th order truncations (pentellation) of the regular 7-cube. There are 32 unique pentellations of the 7-cube with permutations of truncations, cantellations, runcinations, and sterications. 16 are more simply constructed relative to the 7-orthoplex.

7-cube	Pentellated 7-cube	Pentitruncated 7-cube	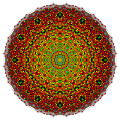Penticantellated 7-cube
Penticantitruncated 7-cube	Pentiruncinated 7-cube	Pentiruncitruncated 7-cube	Pentiruncicantellated 7-cube
Pentiruncicantitruncated 7-cube	Pentistericated 7-cube	Pentisteritruncated 7-cube	Pentistericantellated 7-cube
Pentistericantitruncated 7-cube	Pentisteriruncinated 7-cube	Pentisteriruncitruncated 7-cube	Pentisteriruncicantellated 7-cube
Pentisteriruncicantitruncated 7-cube

Pentellated 7-cube

Pentellated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Small terated hepteract (acronym: stesa) (Jonathan Bowers)^[1]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentitruncated 7-cube

pentitruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Teritruncated hepteract (acronym: tetsa) (Jonathan Bowers)^[2]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Penticantellated 7-cube

Penticantellated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,2,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Terirhombated hepteract (acronym: tersa) (Jonathan Bowers)^[3]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Penticantitruncated 7-cube

penticantitruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,2,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Terigreatorhombated hepteract (acronym: togresa) (Jonathan Bowers)^[4]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncinated 7-cube

pentiruncinated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,3,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Teriprismated hepteract (acronym: tapsa) (Jonathan Bowers)^[5]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncitruncated 7-cube

pentiruncitruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,3,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Teriprismatotruncated hepteract (acronym: toptasa) (Jonathan Bowers)^[6]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncicantellated 7-cube

pentiruncicantellated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,2,3,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Teriprismatorhombated hepteract (acronym: topresa) (Jonathan Bowers)^[7]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncicantitruncated 7-cube

pentiruncicantitruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,2,3,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Terigreatoprismated hepteract (acronym: togapsa) (Jonathan Bowers)^[8]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph	too complex
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph	too complex	too complex
Dihedral symmetry	[6]	[4]

Pentistericated 7-cube

pentistericated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Tericellated hepteract (acronym: tacosa) (Jonathan Bowers)^[9]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentisteritruncated 7-cube

pentisteritruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Tericellitruncated hepteract (acronym: tecatsa) (Jonathan Bowers)^[10]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentistericantellated 7-cube

pentistericantellated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,2,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Tericellirhombated hepteract (acronym: tecresa) (Jonathan Bowers)^[11]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentistericantitruncated 7-cube

pentistericantitruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,2,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Tericelligreatorhombated hepteract (acronym: tecgresa) (Jonathan Bowers)^[12]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph	too complex
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentisteriruncinated 7-cube

Pentisteriruncinated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,3,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Bipenticantitruncated 7-cube as t_1,2,3,6{4,3⁵}
• Tericelliprismated hepteract (acronym: tecpasa) (Jonathan Bowers)^[13]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentisteriruncitruncated 7-cube

pentisteriruncitruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,3,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges	40320
Vertices	10080
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Tericelliprismatotruncated hepteract (acronym: tecpetsa) (Jonathan Bowers)^[14]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph	too complex
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentisteriruncicantellated 7-cube

pentisteriruncicantellated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,2,3,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges	40320
Vertices	10080
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Bipentiruncicantitruncated 7-cube as t_1,2,3,4,6{4,3⁵}
• Tericelliprismatorhombated hepteract (acronym: tocpresa) (Jonathan Bowers)^[15]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph	too complex
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentisteriruncicantitruncated 7-cube

pentisteriruncicantitruncated 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,2,3,4,5{4,35}
Coxeter-Dynkin diagrams
6-faces
5-faces
4-faces
Cells
Faces
Edges
Vertices
Vertex figure
Coxeter groups	B7, [4,35]
Properties	convex

Alternate names

• Great terated hepteract (acronym: gotesa) (Jonathan Bowers)^[16]

Images

orthographic projections

Coxeter plane	B7 / A6	B6 / D7	B5 / D6 / A4
Graph	too complex
Dihedral symmetry	[14]	[12]	[10]
Coxeter plane	B4 / D5	B3 / D4 / A2	B2 / D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

These polytopes are a part of a set of 127 uniform 7-polytopes with B₇ symmetry.