Polytree

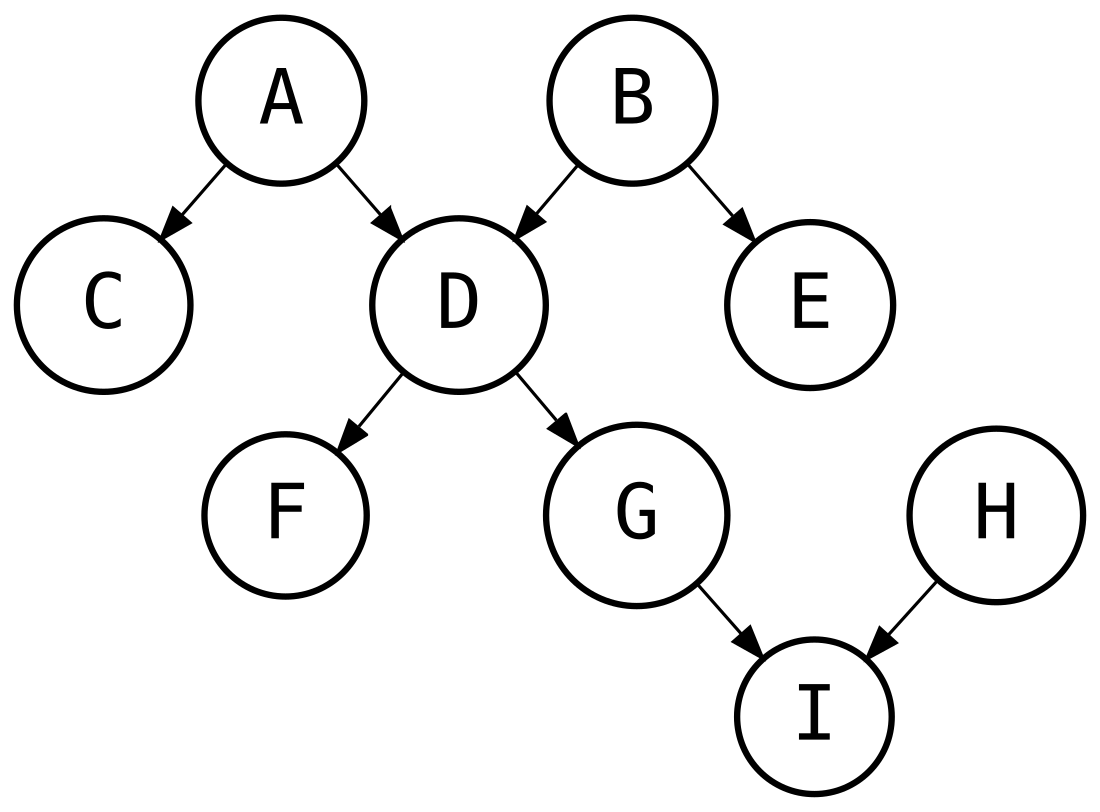
In mathematics, and more specifically in graph theory, a polytree^[1] (also called directed tree,^[2] oriented tree^[3] or singly connected network^[4]) is a directed acyclic graph whose underlying undirected graph is a tree. In other words, if we replace its directed edges with undirected edges, we obtain an undirected graph that is both connected and acyclic. (It is required that no two undirected edges are replaced by the same directed edge; i.e. there must be no pair of vertices linked in the directed graph by edges in both directions.)

A polytree

A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest. In other words, if we replace its directed edges with undirected edges, we obtain an undirected graph that is acyclic.

A polytree is an example of an oriented graph.

The term polytree was coined in 1987 by Rebane and Pearl.^[5]

Related structures

• An arborescence is a directed rooted tree, i.e. a directed acyclic graph in which there exists a single source node that has a unique path to every other node. Every arborescence is a polytree, but not every polytree is an arborescence.
• A multitree is a directed acyclic graph in which the subgraph reachable from any node forms a tree. Every polytree is a multitree.
• The reachability relationship among the nodes of a polytree forms a partial order that has order dimension at most three. If the order dimension is three, there must exist a subset of seven elements ${\displaystyle x}$, ${\displaystyle y_{i}}$, and ${\displaystyle z_{i}}$ (for ${\displaystyle i=0,1,2}$) such that, for each ${\displaystyle i}$, either ${\displaystyle x\leq y_{i}\geq z_{i}}$ or ${\displaystyle x\geq y_{i}\leq z_{i}}$, with these six inequalities defining the polytree structure on these seven elements.^[6]
• A fence or zigzag poset is a special case of a polytree in which the underlying tree is a path and the edges have orientations that alternate along the path. The reachability ordering in a polytree has also been called a generalized fence.^[7]

Enumeration

The number of distinct polytrees on ${\displaystyle n}$ unlabeled nodes, for ${\displaystyle n=1,2,3,\dots }$, is

1, 1, 3, 8, 27, 91, 350, 1376, 5743, 24635, 108968, 492180, ... (sequence A000238 in the OEIS).

Sumner's conjecture

Sumner's conjecture, named after David Sumner, states that tournaments are universal graphs for polytrees, in the sense that every tournament with ${\displaystyle 2n-2}$ vertices contains every polytree with ${\displaystyle n}$ vertices as a subgraph. Although it remains unsolved, it has been proven for all sufficiently large values of ${\displaystyle n}$.^[8]

Applications

Polytrees have been used as a graphical model for probabilistic reasoning.^[1] If a Bayesian network has the structure of a polytree, then belief propagation may be used to perform inference efficiently on it.^[4][5]

The contour tree of a real-valued function on a vector space is a polytree that describes the level sets of the function. The nodes of the contour tree are the level sets that pass through a critical point of the function and the edges describe contiguous sets of level sets without a critical point. The orientation of an edge is determined by the comparison between the function values on the corresponding two level sets.^[9]

See also

• Glossary of graph theory

Notes

1. Dasgupta (1999).
2. Deo (1974), p. 206.
3. Harary & Sumner (1980); Simion (1991).
4. Kim & Pearl (1983).
5. Rebane & Pearl (1987).
6. Trotter & Moore (1977).
7. Ruskey (1989).
8. Kühn, Mycroft & Osthus (2011).
9. Carr, Snoeyink & Axen (2000).

References

• Carr, Hamish; Snoeyink, Jack; Axen, Ulrike (2000), "Computing contour trees in all dimensions", Proc. 11th ACM-SIAM Symposium on Discrete Algorithms (SODA 2000), Association for Computing Machinery, pp. 918–926, ISBN 978-0-89871-453-1
• Dasgupta, Sanjoy (1999), "Learning polytrees" (PDF), Proc. 15th Conference on Uncertainty in Artificial Intelligence (UAI 1999), Stockholm, Sweden, July-August 1999, pp. 134–141.
• Deo, Narsingh (1974), Graph Theory with Applications to Engineering and Computer Science (PDF), Englewood, New Jersey: Prentice-Hall, ISBN 0-13-363473-6.
• Harary, Frank; Sumner, David (1980), "The dichromatic number of an oriented tree", Journal of Combinatorics, Information & System Sciences, 5 (3): 184–187, MR 0603363.
• Kim, Jin H.; Pearl, Judea (1983), "A computational model for causal and diagnostic reasoning in inference engines" (PDF), Proc. 8th International Joint Conference on Artificial Intelligence (IJCAI 1983), Karlsruhe, Germany, August 1983, pp. 190–193.
• Kühn, Daniela; Mycroft, Richard; Osthus, Deryk (2011), "A proof of Sumner's universal tournament conjecture for large tournaments", Proceedings of the London Mathematical Society, Third Series, 102 (4): 731–766, arXiv:1010.4430, doi:10.1112/plms/pdq035, MR 2793448.
• Rebane, George; Pearl, Judea (1987), "The recovery of causal poly-trees from statistical data" (PDF), Proc. 3rd Annual Conference on Uncertainty in Artificial Intelligence (UAI 1987), Seattle, WA, USA, July 1987, pp. 222–228.
• Ruskey, Frank (1989), "Transposition generation of alternating permutations", Order, 6 (3): 227–233, doi:10.1007/BF00563523, MR 1048093.
• Simion, Rodica (1991), "Trees with 1-factors and oriented trees", Discrete Mathematics, 88 (1): 93–104, doi:10.1016/0012-365X(91)90061-6, MR 1099270.
• Trotter, William T. Jr.; Moore, John I. Jr. (1977), "The dimension of planar posets", Journal of Combinatorial Theory, Series B, 22 (1): 54–67, doi:10.1016/0095-8956(77)90048-X.