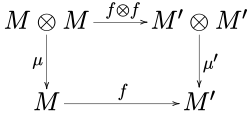Monoid (category theory)

For the algebraic structure, see Monoid.

In category theory, a branch of mathematics, a monoid (or monoid object, or internal monoid, or algebra) ${\displaystyle (M,\mu ,\eta )}$ in a monoidal category ${\displaystyle ({\mathcal {C}},\otimes ,I)}$ is an object ${\displaystyle M}$ together with two morphisms

• ${\displaystyle \mu \colon M\otimes M\to M}$ called multiplication,
• ${\displaystyle \eta \colon I\to M}$ called unit,

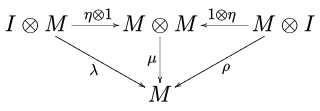
such that the pentagon diagram

and the unitor diagram

commute. In the above notation, ${\displaystyle 1}$ is the identity morphism of ${\displaystyle M}$, ${\displaystyle I}$ is the unit element and ${\displaystyle \alpha ,\lambda }$ and ${\displaystyle \rho }$ are respectively the associator, the left unitor and the right unitor of the monoidal category ${\displaystyle {\mathcal {C}}}$.

Dually, a comonoid in a monoidal category ${\displaystyle {\mathcal {C}}}$ is a monoid in the dual category ${\displaystyle {\mathcal {C}}^{\mathrm {op} }}$.

Suppose that the monoidal category ${\displaystyle {\mathcal {C}}}$ has a braiding ${\displaystyle \gamma }$. A monoid ${\displaystyle M}$ in ${\displaystyle {\mathcal {C}}}$ is commutative when ${\displaystyle \mu \circ \gamma =\mu }$.

Examples

• A monoid object in Set, the category of sets (with the monoidal structure induced by the Cartesian product), is a monoid in the usual sense.
• A monoid object in Top, the category of topological spaces (with the monoidal structure induced by the product topology), is a topological monoid.
• A monoid object in the category of monoids (with the direct product of monoids) is just a commutative monoid. This follows easily from the Eckmann–Hilton argument.
• A monoid object in the category of complete join-semilattices Sup (with the monoidal structure induced by the Cartesian product) is a unital quantale.
• A monoid object in (Ab, ⊗_Z, Z), the category of abelian groups, is a ring.
• For a commutative ring R, a monoid object in
  • (R-Mod, ⊗_R, R), the category of modules over R, is a R-algebra.
  • the category of graded modules is a graded R-algebra.
  • the category of chain complexes of R-modules is a differential graded algebra.
• A monoid object in K-Vect, the category of K-vector spaces (again, with the tensor product), is a unital associative K-algebra, and a comonoid object is a K-coalgebra.
• For any category C, the category [C, C] of its endofunctors has a monoidal structure induced by the composition and the identity functor I_C. A monoid object in [C, C] is a monad on C.
• For any category with a terminal object and finite products, every object becomes a comonoid object via the diagonal morphism Δ_X : X → X × X. Dually in a category with an initial object and finite coproducts every object becomes a monoid object via id_X ⊔ id_X : X ⊔ X → X.

Categories of monoids

Given two monoids (M, μ, η) and (M′, μ′, η′) in a monoidal category C, a morphism f : M → M′ is a morphism of monoids when

• f ∘ μ = μ′ ∘ (f ⊗ f),
• f ∘ η = η′.

In other words, the following diagrams

,

commute.

The category of monoids in C and their monoid morphisms is written Mon_C.^[1]

See also

• Act-S, the category of monoids acting on sets