Kakeya set

In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.

Needle shown rotating inside a deltoid. At every stage of its rotation (except when an endpoint is at a cusp of the deltoid), the needle is in contact with the deltoid at three points: two endpoints (blue) and one tangent point (black). The needle's midpoint (red) describes a circle with diameter equal to half the length of the needle.

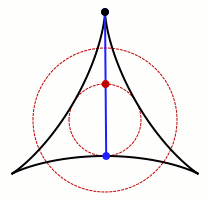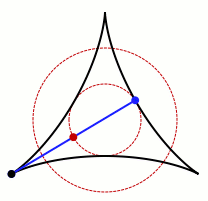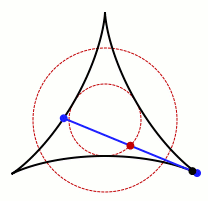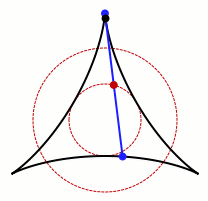
A Kakeya needle set (sometimes also known as a Kakeya set) is a (Besicovitch) set in the plane with a stronger property, that a unit line segment can be rotated continuously through 180 degrees within it, returning to its original position with reversed orientation. Again, the disk of radius 1/2 is an example of a Kakeya needle set.

Kakeya needle problem

The Kakeya needle problem asks whether there is a minimum area of a region ${\displaystyle D}$ in the plane, in which a needle of unit length can be turned through 360°. This question was first posed, for convex regions, by Sōichi Kakeya (1917). The minimum area for convex sets is achieved by an equilateral triangle of height 1 and area 1/√3, as Pál showed.^[1]

Kakeya seems to have suggested that the Kakeya set ${\displaystyle D}$ of minimum area, without the convexity restriction, would be a three-pointed deltoid shape. However, this is false; there are smaller non-convex Kakeya sets.

Besicovitch needle sets

"Sprounting the Perron tree": a method for constructing a Kakeya set of small measure. Shown here are two possible ways of dividing our triangle and overlapping the pieces to get a smaller set, the first if we just use two triangles, and the second if we use eight. The method can be used to construct an arbitrarily small set by cutting up the original triangle to ${\displaystyle 2^{n}}$ pieces. See ^[2] for details.

Besicovitch was able to show that there is no lower bound > 0 for the area of such a region ${\displaystyle D}$, in which a needle of unit length can be turned around. That is, for every ${\displaystyle \varepsilon >0}$, there is region of area ${\displaystyle \varepsilon }$ within which the needle can move through a continuous motion that rotates it a full 360 degrees.^[3] This built on earlier work of his, on plane sets which contain a unit segment in each orientation. Such a set is now called a Besicovitch set. Besicovitch's work showing such a set could have arbitrarily small measure was from 1919. The problem may have been considered by analysts before that.

One method of constructing a Besicovitch set (see figure for corresponding illustrations) is known as a "Perron tree" after Oskar Perron who was able to simplify Besicovitch's original construction.^[4] The precise construction and numerical bounds are given in Besicovitch's popularization.^[2]

The first observation to make is that the needle can move in a straight line as far as it wants without sweeping any area. This is because the needle is a zero width line segment. The second trick of Pál, known as Pál joins^[5] describes how to move the needle between any two locations that are parallel while sweeping negligible area. The needle will follow the shape of an "N". It moves from the first location some distance ${\displaystyle r}$ up the left of the "N", sweeps out the angle to the middle diagonal, moves down the diagonal, sweeps out the second angle, and them moves up the parallel right side of the "N" until it reaches the required second location. The only non-zero area regions swept are the two triangles of height one and the angle at the top of the "N". The swept area is proportional to this angle which is proportional to ${\displaystyle 1/r}$.

The construction starts with any triangle with height 1 and some substantial angle at the top through which the needle can easily sweep. The goal is to do many operations on this triangle to make its area smaller while keeping the directions though which the needle can sweep the same. First consider dividing the triangle in two and translating the pieces over each other so that their bases overlap in a way that minimizes the total area. The needle is able to sweep out the same directions by sweeping out those given by the first triangle, jumping over to the second, and then sweeping out the directions given by the second. The needle can jump triangles using the "N" technique because the two lines at which the original triangle was cut are parallel.

Now, suppose we divide our triangle into 2ⁿ subtriangles. The figure shows eight. For each consecutive pair of triangles, perform the same overlapping operation we described before to get half as many new shapes, each consisting of two overlapping triangles. Next, overlap consecutive pairs of these new shapes by shifting them so that their bases overlap in a way that minimizes the total area. Repeat this n times until there is only one shape. Again, the needle is able to sweep out the same directions by sweeping those out in each of the 2ⁿ subtriangles in order of their direction. The needle can jump consecutive triangles using the "N" technique because the two lines at which these triangle were cut are parallel.

What remains is to compute the area of the final shape. The proof is too hard to present here. Instead, we will just argue how the numbers might go. Looking at the figure, one sees that the 2ⁿ subtriangles overlap a lot. All of them overlap at the bottom, half of them at the bottom of the left branch, a quarter of them at the bottom of the left left branch, and so on. Suppose that the area of each shape created with i merging operations from 2ⁱ subtriangles is bounded by A_i. Before merging two of these shapes, they have area bounded be 2A_i. Then we move the two shapes together in the way that overlaps them as much as possible. In a worst case, these two regions are two 1 by ε rectangles perpendicular to each other so that they overlap at an area of only ε². But the two shapes that we have constructed, if long and skinny, point in much of the same direction because they are made from consecutive groups of subtriangles. The handwaving states that they over lap by at least 1% of their area. Then the merged area would be bounded by A_i+1 = 1.99 A_i. The area of the original triangle is bounded by 1. Hence, the area of each subtriangle is bounded by A₀ = 2^-n and the final shape has area bounded by A_n = 1.99ⁿ × 2^-n. In actuality, a careful summing up all areas that do not overlap gives that the area of the final region is much bigger, namely, 1/n. As n grows, this area shrinks to zero. A Besicovitch set can be created by combining six rotations of a Perron tree created from an equilateral triangle. A similar construction can be made with parallelograms

There are other methods for constructing Besicovitch sets of measure zero aside from the 'sprouting' method. For example, Kahane uses Cantor sets to construct a Besicovitch set of measure zero in the two-dimensional plane.^[6]

A Kakeya needle set constructed from Perron trees.

In 1941, H. J. Van Alphen^[7] showed that there are arbitrary small Kakeya needle sets inside a circle with radius 2 + ε (arbitrary ε > 0). Simply connected Kakeya needle sets with smaller area than the deltoid were found in 1965. Melvin Bloom and I. J. Schoenberg independently presented Kakeya needle sets with areas approaching to ${\displaystyle {\tfrac {\pi }{24}}(5-2{\sqrt {2}})}$, the Bloom-Schoenberg number. Schoenberg conjectured that this number is the lower bound for the area of simply connected Kakeya needle sets. However, in 1971, F. Cunningham^[8] showed that, given ε > 0, there is a simply connected Kakeya needle set of area less than ε contained in a circle of radius 1.

Although there are Kakeya needle sets of arbitrarily small positive measure and Besicovich sets of measure 0, there are no Kakeya needle sets of measure 0.

Kakeya conjecture

Statement

The same question of how small these Besicovitch sets could be was then posed in higher dimensions, giving rise to a number of conjectures known collectively as the Kakeya conjectures, and have helped initiate the field of mathematics known as geometric measure theory. In particular, if there exist Besicovitch sets of measure zero, could they also have s-dimensional Hausdorff measure zero for some dimension s less than the dimension of the space in which they lie? This question gives rise to the following conjecture:

Kakeya set conjecture: Define a Besicovitch set in Rⁿ to be a set which contains a unit line segment in every direction. Is it true that such sets necessarily have Hausdorff dimension and Minkowski dimension equal to n?

This is known to be true for n = 1, 2 but only partial results are known in higher dimensions.

Kakeya maximal function

A modern way of approaching this problem is to consider a particular type of maximal function, which we construct as follows: Denote Sⁿ⁻¹ ⊂ Rⁿ to be the unit sphere in n-dimensional space. Define ${\displaystyle T_{e}^{\delta }(a)}$ to be the cylinder of length 1, radius δ > 0, centered at the point a ∈ Rⁿ, and whose long side is parallel to the direction of the unit vector e ∈ Sⁿ⁻¹. Then for a locally integrable function f, we define the Kakeya maximal function of f to be

${\displaystyle f_{*}^{\delta }(e)=\sup _{a\in \mathbf {R} ^{n}}{\frac {1}{m(T_{e}^{\delta }(a))}}\int _{T_{e}^{\delta }(a)}|f(y)|dm(y)}$

where m denotes the n-dimensional Lebesgue measure. Notice that ${\displaystyle f_{*}^{\delta }}$ is defined for vectors e in the sphere Sⁿ⁻¹.

Then there is a conjecture for these functions that, if true, will imply the Kakeya set conjecture for higher dimensions:

Kakeya maximal function conjecture: For all ε > 0, there exists a constant C_ε > 0 such that for any function f and all δ > 0, (see lp space for notation)

${\displaystyle \left\|f_{*}^{\delta }\right\|_{L^{n}(\mathbf {S} ^{n-1})}\leqslant C_{\epsilon }\delta ^{-\epsilon }\|f\|_{L^{n}(\mathbf {R} ^{n})}.}$

Results

Some results toward proving the Kakeya conjecture are the following:

• The Kakeya conjecture is true for n = 1 (trivially) and n = 2 (Davies^[9]).
• In any n-dimensional space, Wolff^[10] showed that the dimension of a Kakeya set must be at least (n+2)/2.
• In 2002, Katz and Tao^[11] improved Wolff's bound to ${\displaystyle (2-{\sqrt {2}})(n-4)+3}$, which is better for n > 4.
• In 2000, Katz, Łaba, and Tao^[12] proved that the Minkowski dimension of Kakeya sets in 3 dimensions is strictly greater than 5/2.
• In 2000, Jean Bourgain connected the Kakeya problem to arithmetic combinatorics^[13][14] which involves harmonic analysis and additive number theory.
• In 2017, Katz and Zahl^[15] improved the lower bound on the Hausdorff dimension of Besicovitch sets in 3 dimensions to ${\displaystyle 5/2+\epsilon }$ for an absolute constant ${\displaystyle \epsilon >0}$.

Applications to analysis

Somewhat surprisingly, these conjectures have been shown to be connected to a number of questions in other fields, notably in harmonic analysis. For instance, in 1971, Charles Fefferman was able to use the Besicovitch set construction to show that in dimensions greater than 1, truncated Fourier integrals taken over balls centered at the origin with radii tending to infinity need not converge in L^p norm when p ≠ 2 (this is in contrast to the one-dimensional case where such truncated integrals do converge).^[16]

Analogues and generalizations of the Kakeya problem

Sets containing circles and spheres

Analogues of the Kakeya problem include considering sets containing more general shapes than lines, such as circles.

• In 1997^[17] and 1999,^[18] Wolff proved that sets containing a sphere of every radius must have full dimension, that is, the dimension is equal to the dimension of the space it is lying in, and proved this by proving bounds on a circular maximal function analogous to the Kakeya maximal function.

• It was conjectured that there existed sets containing a sphere around every point of measure zero. Results of Elias Stein^[19] proved all such sets must have positive measure when n ≥ 3, and Marstrand^[20] proved the same for the case n=2.

Sets containing k-dimensional disks

A generalization of the Kakeya conjecture is to consider sets that contain, instead of segments of lines in every direction, but, say, portions of k-dimensional subspaces. Define an (n, k)-Besicovitch set K to be a compact set in Rⁿ containing a translate of every k-dimensional unit disk which has Lebesgue measure zero. That is, if B denotes the unit ball centered at zero, for every k-dimensional subspace P, there exists x ∈ Rⁿ such that (P ∩ B) + x ⊆ K. Hence, a (n, 1)-Besicovitch set is the standard Besicovitch set described earlier.

The (n, k)-Besicovitch conjecture: There are no (n, k)-Besicovitch sets for k > 1.

In 1979, Marstrand^[21] proved that there were no (3, 2)-Besicovitch sets. At around the same time, however, Falconer^[22] proved that there were no (n, k)-Besicovitch sets for 2k > n. The best bound to date is by Bourgain,^[23] who proved in that no such sets exist when 2^k−1 + k > n.

Kakeya sets in vector spaces over finite fields

In 1999, Wolff posed the finite field analogue to the Kakeya problem, in hopes that the techniques for solving this conjecture could be carried over to the Euclidean case.

Finite Field Kakeya Conjecture: Let F be a finite field, let K ⊆ Fⁿ be a Kakeya set, i.e. for each vector y ∈ Fⁿ there exists x ∈ Fⁿ such that K contains a line {x + ty : t ∈ F}. Then the set K has size at least c_n|F|ⁿ where c_n>0 is a constant that only depends on n.

Zeev Dvir proved this conjecture in 2008, showing that the statement holds for c_n = 1/n!.^[24][25] In his proof, he observed that any polynomial in n variables of degree less than |F| vanishing on a Kakeya set must be identically zero. On the other hand, the polynomials in n variables of degree less than |F| form a vector space of dimension

${\displaystyle {|\mathbf {F} |+n-1 \choose n}\geq {\frac {|\mathbf {F} |^{n}}{n!}}.}$

Therefore, there is at least one non-trivial polynomial of degree less than |F| that vanishes on any given set with less than this number of points. Combining these two observations shows that Kakeya sets must have at least |F|ⁿ/n! points.

It is not clear whether the techniques will extend to proving the original Kakeya conjecture but this proof does lend credence to the original conjecture by making essentially algebraic counterexamples unlikely. Dvir has written a survey article on progress on the finite field Kakeya problem and its relationship to randomness extractors.^[26]

See also

• Nikodym set

Notes

1. Pal, Julius (1920). "Ueber ein elementares variationsproblem". Kongelige Danske Videnskabernes Selskab Math.-Fys. Medd. 2: 1–35.
2. Besicovitch, A. S. (August 1963). "The Kakeya Problem". The American Mathematical Monthly. 70 (7): 697. doi:10.2307/2312249. ISSN 0002-9890.
3. Besicovitch, Abram (1919). "Sur deux questions d'integrabilite des fonctions". J. Soc. Phys. Math. 2: 105–123.
   Besicovitch, Abram (1928). "On Kakeya's problem and a similar one". Mathematische Zeitschrift. 27: 312–320. doi:10.1007/BF01171101. S2CID 121781065.
4. Perron, O. (1928). "Über einen Satz von Besicovitch". Mathematische Zeitschrift. 28: 383–386. doi:10.1007/BF01181172. S2CID 120768630.
   Falconer, K. J. (1985). The Geometry of Fractal Sets. Cambridge University Press. pp. 96–99.
5. The Kakeya Problem Archived 2015-07-15 at the Wayback Machine by Markus Furtner
6. Kahane, Jean-Pierre (1969). "Trois notes sur les ensembles parfaits linéaires". Enseignement Math. 15: 185–192.
7. Alphen, H. J. (1942). "Uitbreiding van een stelling von Besicovitch". Mathematica Zutphen B. 10: 144–157.
8. Cunningham, F. (1971). "The Kakeya problem for simply connected and for star-shaped sets" (PDF). American Mathematical Monthly. 78 (2). The American Mathematical Monthly, Vol. 78, No. 2: 114–129. doi:10.2307/2317619. JSTOR 2317619.
9. Davies, Roy (1971). "Some remarks on the Kakeya problem". Proc. Cambridge Philos. Soc. 69 (3): 417–421. Bibcode:1971PCPS...69..417D. doi:10.1017/S0305004100046867.
10. Wolff, Thomas (1995). "An improved bound for Kakeya type maximal functions". Rev. Mat. Iberoamericana. 11: 651–674. doi:10.4171/rmi/188.
11. Katz, Nets Hawk; Tao, Terence (2002). "New bounds for Kakeya problems". Journal d'Analyse Mathématique. 87: 231–263. arXiv:math/0102135. doi:10.1007/BF02868476. S2CID 119644987.
12. Katz, Nets Hawk; Łaba, Izabella; Tao, Terence (September 2000). "An Improved Bound on the Minkowski Dimension of Besicovitch Sets in ${\displaystyle \mathbb {R} ^{3}}$". The Annals of Mathematics. 152 (2): 383–446. arXiv:math/0004015. doi:10.2307/2661389. JSTOR 2661389. S2CID 17007027.
13. J. Bourgain, Harmonic analysis and combinatorics: How much may they contribute to each other?, Mathematics: Frontiers and Perspectives, IMU/Amer. Math. Soc., 2000, pp. 13–32.
14. Tao, Terence (March 2001). "From Rotating Needles to Stability of Waves: Emerging Connections between Combinatorics, Analysis and PDE" (PDF). Notices of the AMS. 48 (3): 297–303.
15. Katz, Nets Hawk; Zahl, Joshua (2019). "An improved bound on the Hausdorff dimension of Besicovitch sets in ${\displaystyle \mathbb {R} ^{3}}$". Journal of the American Mathematical Society. 32 (1): 195–259. arXiv:1704.07210. doi:10.1090/jams/907. S2CID 119322412.
16. Fefferman, Charles (1971). "The multiplier problem for the ball". Annals of Mathematics. 94 (2): 330–336. doi:10.2307/1970864. JSTOR 1970864.
17. Wolff, Thomas (1997). "A Kakeya problem for circles". American Journal of Mathematics. 119 (5): 985–1026. doi:10.1353/ajm.1997.0034. S2CID 120122372.
18. Wolff, Thomas; Wolff, Thomas (1999). "On some variants of the Kakeya problem" (PDF). Pacific Journal of Mathematics. 190: 111–154. doi:10.2140/pjm.1999.190.111.
19. Stein, Elias (1976). "Maximal functions: Spherical means". Proc. Natl. Acad. Sci. U.S.A. 73 (7): 2174–2175. Bibcode:1976PNAS...73.2174S. doi:10.1073/pnas.73.7.2174. PMC 430482. PMID 16592329.
20. Marstrand, J. M. (1987). "Packing circles in the plane". Proceedings of the London Mathematical Society. 55: 37–58. doi:10.1112/plms/s3-55.1.37.
21. Marstrand, J. M. (1979). "Packing Planes in ${\displaystyle \mathbb {R} ^{3}}$". Mathematika. 26 (2): 180–183. doi:10.1112/S0025579300009748.
22. Falconer, K. J. (1980). "Continuity properties of k-plane integrals and Besicovitch sets". Math. Proc. Cambridge Philos. Soc. 87 (2): 221–226. Bibcode:1980MPCPS..87..221F. doi:10.1017/S0305004100056681.
23. Bourgain, Jean (1997). "Besicovitch type maximal operators and applications to Fourier analysis". Geometric and Functional Analysis. 1 (2): 147–187. doi:10.1007/BF01896376. S2CID 122038469.
24. Dvir, Z. (2009). "On the size of Kakeya sets in finite fields". Journal of the American Mathematical Society. 22 (4): 1093–1097. arXiv:0803.2336. Bibcode:2009JAMS...22.1093D. doi:10.1090/S0894-0347-08-00607-3. S2CID 3358826.
25. Terence Tao (2008-03-24). "Dvir's proof of the finite field Kakeya conjecture". What's New. Retrieved 2008-04-08.
26. Dvir, Zeev (2009). "From Randomness Extraction to Rotating Needles". ACM SIGACT News. ECCC TR09-077..

References

• Besicovitch, Abram (1963). "The Kakeya Problem". American Mathematical Monthly. 70 (7): 697–706. doi:10.2307/2312249. JSTOR 2312249. MR 0157266.
• Dvir, Zeev (2009). "On the size of Kakeya sets in finite fields". Journal of the American Mathematical Society. 22 (4): 1093–1097. arXiv:0803.2336. Bibcode:2009JAMS...22.1093D. doi:10.1090/S0894-0347-08-00607-3. MR 2525780. S2CID 3358826.
• Falconer, Kenneth J. (1985). The Geometry of Fractal Sets. Cambridge Tracts in Mathematics. Vol. 85. Cambridge: Cambridge University Press. ISBN 0-521-25694-1. MR 0867284.
• Kakeya, Soichi (1917). "Some problems on maximum and minimum regarding ovals". Tohoku Science Reports. 6: 71–88.
• Katz, Nets Hawk; Łaba, Izabella; Tao, Terence (2000). "An improved bound on the Minkowski dimension of Besicovitch sets in ${\displaystyle \mathbf {R} ^{3}}$" (PDF). Annals of Mathematics. 152 (2): 383–446. doi:10.2307/2661389. JSTOR 2661389. MR 1804528. S2CID 17007027.

• Wolff, Thomas (1999). "Recent work connected with the Kakeya problem". In Rossi, Hugo (ed.). Prospects in Mathematics: Invited Talks on the Occasion of the 250th Anniversary of Princeton University. Providence, RI: American Mathematical Society. pp. 129–162. ISBN 978-0-8218-0975-4. MR 1660476.
• Wolff, Thomas (2003). Łaba, Izabella; Shubin, Carol (eds.). Lectures on Harmonic Analysis. University Lecture Series. Vol. 29. With a foreword by Charles Fefferman and preface by Izabella Łaba. Providence, RI: American Mathematical Society. doi:10.1090/ulect/029. ISBN 0-8218-3449-5. MR 2003254.

External links

• Kakeya at University of British Columbia
• Besicovitch at UCLA
• Kakeya needle problem at mathworld
• Dvir's proof of the finite field Kakeya conjecture at Terence Tao's blog
• An Introduction to Besicovitch-Kakeya Sets