List of k-uniform tilings

A k-uniform tiling is a tiling of tilings of the plane by convex regular polygons, connected edge-to-edge, with k types of vertices. The 1-uniform tiling include 3 regular tilings, and 8 semiregular tilings. A 1-uniform tiling can be defined by its vertex configuration. Higher k-uniform tilings are listed by their vertex figures, but are not generally uniquely identified this way.

Example k-uniform tilings

1-uniform (regular)	1-uniform (semiregular)
2-uniform tiling	3-uniform tiling

The complete lists of k-uniform tilings have been enumerated up to k=6. There are 20 2-uniform tilings, 61 3-uniform tilings, 151 4-uniform tilings, 332 5-uniform tilings, and 673 6-uniform tilings. This article lists all solutions up to k=5.

This square tiling is isogonal and isohedral, but not uniform because it is not edge-to-edge.

Other tilings of regular polygons that are not edge-to-edge allow different sized polygons, and continuous shifting positions of contact.

Classification

3-uniform tiling #57 of 61 colored

by sides, yellow triangles, red squares (by polygons)

by 4-isohedral positions, 3 shaded colors of triangles (by orbits)

Such periodic tilings of convex polygons may be classified by the number of orbits of vertices, edges and tiles. If there are k orbits of vertices, a tiling is known as k-uniform or k-isogonal; if there are t orbits of tiles, as t-isohedral; if there are e orbits of edges, as e-isotoxal.

k-uniform tilings with the same vertex figures can be further identified by their wallpaper group symmetry.

Enumeration

1-uniform tilings include 3 regular tilings, and 8 semiregular ones, with 2 or more types of regular polygon faces. There are 20 2-uniform tilings, 61 3-uniform tilings, 151 4-uniform tilings, 332 5-uniform tilings and 673 6-uniform tilings. Each can be grouped by the number m of distinct vertex figures, which are also called m-Archimedean tilings.^[1]

Finally, if the number of types of vertices is the same as the uniformity (m = k below), then the tiling is said to be Krotenheerdt. In general, the uniformity is greater than or equal to the number of types of vertices (m ≥ k), as different types of vertices necessarily have different orbits, but not vice versa. Setting m = n = k, there are 11 such tilings for n = 1; 20 such tilings for n = 2; 39 such tilings for n = 3; 33 such tilings for n = 4; 15 such tilings for n = 5; 10 such tilings for n = 6; and 7 such tilings for n = 7.

k-uniform, m-Archimedean tiling counts^[2]

		m-Archimedean
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	≥ 15	Total
k-uniform	1	11	0														11
	2	0	20	0													20
	3	0	22	39	0												61
	4	0	33	85	33	0											151
	5	0	74	149	94	15	0										332
	6	0	100	284	187	92	10	0									673
	7	0	?	?	?	?	?	7	0								?
	8	0	?	?	?	?	?	20	0	0							?
	9	0	?	?	?	?	?	?	8	0	0						?
	10	0	?	?	?	?	?	?	27	0	0	0					?
	11	0	?	?	?	?	?	?	?	1	0	0	0				?
	12	0	?	?	?	?	?	?	?	?	0	0	0	0			?
	13	0	?	?	?	?	?	?	?	?	?	?	?	0	0		?
	14	0	?	?	?	?	?	?	?	?	?	?	?	?	0	0	?
	≥ 15	0	?	?	?	?	?	?	?	?	?	?	?	?	?	0	?
	Total	11	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	0	∞

1-uniform tilings (regular)

A tiling is said to be regular if the symmetry group of the tiling acts transitively on the flags of the tiling, where a flag is a triple consisting of a mutually incident vertex, edge and tile of the tiling. This means that, for every pair of flags, there is a symmetry operation mapping the first flag to the second. This is equivalent to the tiling being an edge-to-edge tiling by congruent regular polygons. There must be six equilateral triangles, four squares or three regular hexagons at a vertex, yielding the three regular tessellations.

Further information: List_of_regular_polytopes_and_compounds § Euclidean_tilings

Regular tilings (3)

p6m, *632		p4m, *442
36 (t=1, e=1)	63 (t=1, e=1)	44 (t=1, e=1)

m-Archimedean and k-uniform tilings

Further information: List of convex uniform tilings

Vertex-transitivity means that for every pair of vertices there is a symmetry operation mapping the first vertex to the second.^[3]

If the requirement of flag-transitivity is relaxed to one of vertex-transitivity, while the condition that the tiling is edge-to-edge is kept, there are eight additional tilings possible, known as Archimedean, uniform or demiregular tilings. Note that there are two mirror image (enantiomorphic or chiral) forms of 3⁴.6 (snub hexagonal) tiling, only one of which is shown in the following table. All other regular and semiregular tilings are achiral.

Grünbaum and Shephard distinguish the description of these tilings as Archimedean as referring only to the local property of the arrangement of tiles around each vertex being the same, and that as uniform as referring to the global property of vertex-transitivity. Though these yield the same set of tilings in the plane, in other spaces there are Archimedean tilings which are not uniform.

1-uniform tilings (semiregular)

Uniform tilings (8)

p6m, *632
[ 3.122] (t=2, e=2)	[ 3.4.6.4] (t=3, e=2)	[ 4.6.12] (t=3, e=3)	[ (3.6)2] (t=2, e=1)
[ 4.82] (t=2, e=2)	[ 32.4.3.4] (t=2, e=2)	[ 33.42] (t=2, e=3)	[ 34.6] (t=3, e=3)

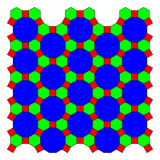
2-uniform tilings

There are twenty (20) 2-uniform tilings of the Euclidean plane. (also called 2-isogonal tilings or demiregular tilings)^[4][5][6] Vertex types are listed for each. If two tilings share the same two vertex types, they are given subscripts 1,2.

2-uniform tilings (20)

p6m, *632						p4m, *442
[36; 32.4.3.4 (t=3, e=3)	[3.4.6.4; 32.4.3.4 (t=4, e=4)	[3.4.6.4; 33.42] (t=4, e=4)	[3.4.6.4; 3.42.6] (t=5, e=5)	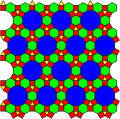[4.6.12; 3.4.6.4] (t=4, e=4)	[36; 32.4.12] (t=4, e=4)	[3.12.12; 3.4.3.12] (t=3, e=3)
p6m, *632	p6, 632	p6, 632	cmm, 2*22	pmm, *2222	cmm, 2*22	pmm, *2222
[36; 32.62] (t=2, e=3)	[36; 34.6]1 (t=3, e=3)	[36; 34.6]2 (t=5, e=7)	[32.62; 34.6] (t=2, e=4)	[3.6.3.6; 32.62] (t=2, e=3)	[3.42.6; 3.6.3.6]2 (t=3, e=4)	[3.42.6; 3.6.3.6]1 (t=4, e=4)
p4g, 4*2	pgg, 22×	cmm, 2*22	cmm, 2*22	pmm, *2222	cmm, 2*22
[33.42; 32.4.3.4]1 (t=4, e=5)	[33.42; 32.4.3.4]2 (t=3, e=6)	[44; 33.42]1 (t=2, e=4)	[44; 33.42]2 (t=3, e=5)	[36; 33.42]1 (t=3, e=4)	[36; 33.42]2 (t=4, e=5)

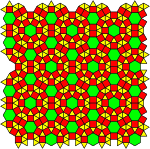
3-uniform tilings

There are 61 3-uniform tilings of the Euclidean plane. 39 are 3-Archimedean with 3 distinct vertex types, while 22 have 2 identical vertex types in different symmetry orbits. Chavey (1989)

3-uniform tilings, 3 vertex types

3-uniform tilings with 3 vertex types (39)

[3.426; 3.6.3.6; 4.6.12] (t=6, e=7)	[36; 324.12; 4.6.12] (t=5, e=6)	[324.12; 3.4.6.4; 3.122] (t=5, e=6)	[3.4.3.12; 3.4.6.4; 3.122] (t=5, e=6)	[3342; 324.12; 3.4.6.4] (t=6, e=8)
[36; 3342; 324.12] (t=6, e=7)	[36; 324.3.4; 324.12] (t=5, e=6)	[346; 3342; 324.3.4] (t=5, e=6)	[36; 324.3.4; 3.426] (t=5, e=6)	[36; 324.3.4; 3.4.6.4] (t=5, e=6)
[36; 3342; 3.4.6.4] (t=6, e=6)	[36; 324.3.4; 3.4.6.4] (t=6, e=6)	[36; 3342; 324.3.4] (t=4, e=5)	[324.12; 3.4.3.12; 3.122] (t=4, e=7)	[3.4.6.4; 3.426; 44] (t=3, e=4)
[324.3.4; 3.4.6.4; 3.426] (t=4, e=6)	[3342; 324.3.4; 44] (t=4, e=6)	[3.426; 3.6.3.6; 44] (t=5, e=7)	[3.426; 3.6.3.6; 44] (t=6, e=7)	[3.426; 3.6.3.6; 44] (t=4, e=5)
[3.426; 3.6.3.6; 44] (t=5, e=6)	[3342; 3262; 3.426] (t=5, e=8)	[3262; 3.426; 3.6.3.6] (t=4, e=7)	[3262; 3.426; 3.6.3.6] (t=5, e=7)	[346; 3342; 3.426] (t=5, e=7)
[3262; 3.6.3.6; 63] (t=4, e=5)	[3262; 3.6.3.6; 63] (t=2, e=4)	[346; 3262; 63] (t=2, e=5)	[36; 3262; 63] (t=2, e=3)	[36; 346; 3262] (t=5, e=8)
[36; 346; 3262] (t=3, e=5)	[36; 346; 3262] (t=3, e=6)	[36; 346; 3.6.3.6] (t=5, e=6)	[36; 346; 3.6.3.6] (t=4, e=4)	[36; 346; 3.6.3.6] (t=3, e=3)
[36; 3342; 44] (t=4, e=6)	[36; 3342; 44] (t=5, e=7)	[36; 3342; 44] (t=3, e=5)	[36; 3342; 44] (t=4, e=6)

3-uniform tilings, 2 vertex types (2:1)

3-uniform tilings (2:1) (22)

[(3.4.6.4)2; 3.426] (t=6, e=6)	[(36)2; 346] (t=3, e=4)	[(36)2; 346] (t=5, e=5)	[(36)2; 346] (t=7, e=9)	[36; (346)2] (t=4, e=6)
[36; (324.3.4)2] (t=4, e=5)	[(3.426)2; 3.6.3.6] (t=6, e=8)	[3.426; (3.6.3.6)2] (t=4, e=6)	[3.426; (3.6.3.6)2] (t=5, e=6)	[3262; (3.6.3.6)2] (t=3, e=5)
[(346)2; 3.6.3.6] (t=4, e=7)	[(346)2; 3.6.3.6] (t=4, e=7)	[3342; (44)2] (t=4, e=7)	[(3342)2; 44] (t=5, e=7)	[3342; (44)2] (t=3, e=6)
[(3342)2; 44] (t=4, e=6)	[(3342)2; 324.3.4] (t=5, e=8)	[3342; (324.3.4)2] (t=6, e=9)	[36; (3342)2] (t=5, e=7)	[36; (3342)2] (t=4, e=6)
[(36)2; 3342] (t=6, e=7)	[(36)2; 3342] (t=5, e=6)

4-uniform tilings

There are 151 4-uniform tilings of the Euclidean plane. Brian Galebach's search reproduced Krotenheerdt's list of 33 4-uniform tilings with 4 distinct vertex types, as well as finding 85 of them with 3 vertex types, and 33 with 2 vertex types.

4-uniform tilings, 4 vertex types

There are 33 with 4 types of vertices.

4-uniform tilings with 4 vertex types (33)

[33434; 3262; 3446; 63]	[3342; 3262; 3446; 46.12]	[33434; 3262; 3446; 46.12]	[36; 3342; 33434; 334.12]	[36; 33434; 334.12; 3.122]
[36; 33434; 343.12; 3.122]	[36; 3342; 33434; 3464]	[36; 3342; 33434; 3464]	[36; 33434; 3464; 3446]	[346; 3262; 3636; 63]
[346; 3262; 3636; 63]	[334.12; 343.12; 3464; 46.12]	[3342; 334.12; 343.12; 3.122]	[3342; 334.12; 343.12; 44]	[3342; 334.12; 343.12; 3.122]
[36; 3342; 33434; 44]	[33434; 3262; 3464; 3446]	[36; 3342; 3446; 3636]	[36; 346; 3446; 3636]	[36; 346; 3446; 3636]
[36; 346; 3342; 3446]	[36; 346; 3342; 3446]	[36; 346; 3262; 63]	[36; 346; 3262; 63]	[36; 346; 3262; 63]
[36; 346; 3262; 63]	[36; 346; 3262; 3636]	[3342; 3262; 3446; 63]	[3342; 3262; 3446; 63]	[3262; 3446; 3636; 44]
[3262; 3446; 3636; 44]	[3262; 3446; 3636; 44]	[3262; 3446; 3636; 44]

4-uniform tilings, 3 vertex types (2:1:1)

There are 85 with 3 types of vertices.

4-uniform tilings (2:1:1)

[3464; (3446)2; 46.12]	[3464; 3446; (46.12)2]	[334.12; 3464; (3.122)2]	[343.12; 3464; (3.122)2]	[33434; 343.12; (3464)2]
[(36)2; 3342; 334.12]	[(3464)2; 3446; 3636]	[3464; 3446; (3636)2]	[3464; (3446)2; 3636]	[(36)2; 3342; 33434]
[(36)2; 3342; 33434]	[36; 3262; (63)2]	[36; 3262; (63)2]	[36; (3262)2; 63]	[36; (3262)2; 63]
[36; 3262; (63)2]	[36; 3262; (63)2]	[36; (346)2; 3262]	[36; (3262)2; 3636]	[(346)2; 3262; 63]
[(346)2; 3262; 63]	[346; 3262; (3636)2]	[346; 3262; (3636)2]	[3342; 33434; (3464)2]	[36; 33434; (3464)2]
[36; (33434)2; 3464]	[36; (3342)2; 3464]	[(3464)2; 3446; 3636]	[346; (33434)2; 3446]	[36; 3342; (33434)2]
[36; 3342; (33434)2]	[(3342)2; 33434; 44]	[(3342)2; 33434; 44]	[3464; (3446)2; 44]	[33434; (334.12)2; 343.12]
[36; (3262)2; 63]	[36; (3262)2; 63]	[36; 346; (3262)2]	[(36)2; 346; 3262]	[(36)2; 346; 3262]
[(36)2; 346; 3636]	[346; (3262)2; 3636]	[346; (3262)2; 3636]	[(346)2; 3262; 3636]	[(346)2; 3262; 3636]
[36; 346; (3636)2]	[3262; (3636)2; 63]	[3262; (3636)2; 63]	[(3262)2; 3636; 63]	[3262; 3636; (63)2]
[346; 3262; (63)2]	[346; (3262)2; 3636]	[3262; 3446; (3636)2]	[3262; 3446; (3636)2]	[346; (3342)2; 3636]
[346; (3342)2; 3636]	[346; 3342; (3446)2]	[3446; 3636; (44)2]	[3446; 3636; (44)2]	[3446; 3636; (44)2]
[3446; 3636; (44)2]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]
[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[3446; (3636)2; 44]
[3446; (3636)2; 44]	[3446; (3636)2; 44]	[3446; (3636)2; 44]	[36; 3342; (44)2]	[36; 3342; (44)2]
[36; (3342)2; 44]	[36; 3342; (44)2]	[36; 3342; (44)2]	[36; (3342)2; 44]	[36; (3342)2; 44]
[36; (3342)2; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]

4-uniform tilings, 2 vertex types (2:2) and (3:1)

There are 33 with 2 types of vertices, 12 with two pairs of types, and 21 with 3:1 ratio of types.

4-uniform tilings (2:2)

[(3464)2; (46.12)2]	[(33434)2; (3464)2]	[(33434)2; (3464)2]	[(346)2; (3636)2]	[(36)2; (346)2]
[(3342)2; (33434)2]	[(3342)2; (44)2]	[(3342)2; (44)2]	[(3342)2; (44)2]	[(36)2; (3342)2]
[(36)2; (3342)2]	[(36)2; (3342)2]

4-uniform tilings (3:1)

[343.12; (3.122)3]	[(346)3; 3636]	[36; (346)3]	[(36)3; 346]	[(36)3; 346]
[(3342)3; 33434]	[3342; (33434)3]	[3446; (3636)3]	[3446; (3636)3]	[3262; (3636)3]
[3262; (3636)3]	[3342; (44)3]	[3342; (44)3]	[(3342)3; 44]	[(3342)3; 44]
[(3342)3; 44]	[36; (3342)3]	[36; (3342)3]	[36; (3342)3]	[(36)3; 3342]
[(36)3; 3342]

5-uniform tilings

There are 332 5-uniform tilings of the Euclidean plane. Brian Galebach's search identified 332 5-uniform tilings, with 2 to 5 types of vertices. There are 74 with 2 vertex types, 149 with 3 vertex types, 94 with 4 vertex types, and 15 with 5 vertex types.

5-uniform tilings, 5 vertex types

There are 15 5-uniform tilings with 5 unique vertex figure types.

5-uniform tilings, 5 types

[33434; 3262; 3464; 3446; 63]	[36; 346; 3262; 3636; 63]	[36; 346; 3342; 3446; 46.12]	[346; 3342; 33434; 3446; 44]	[36; 33434; 3464; 3446; 3636]
[36; 346; 3464; 3446; 3636]	[33434; 334.12; 3464; 3.12.12; 46.12]	[36; 346; 3446; 3636; 44]	[36; 346; 3446; 3636; 44]	[36; 346; 3446; 3636; 44]
[36; 346; 3446; 3636; 44]	[36; 3342; 3446; 3636; 44]	[36; 346; 3342; 3446; 44]	[36; 3342; 3262; 3446; 3636]	[36; 346; 3342; 3262; 3446]

5-uniform tilings, 4 vertex types (2:1:1:1)

There are 94 5-uniform tilings with 4 vertex types.

5-uniform tilings (2:1:1:1)

[36; 33434; (3446)2; 46.12]	[36; 33434; 3446; (46.12)2]	[36; 33434; 3464; (46.12)2]	[36; 3342; (334.12)2; 3464]	[36; (3342)2; 334.12; 3464]
[36; 33434; (334.12)2; 3464]	[36; 33434; 334.12; (3.12.12)2]	[36; 346; (3342)2; 334.12]	[36; 33434; 343.12; (3.12.12)2]	[(3342)2; 334.12; 343.12; 3.12.12]
[(3342)2; 334.12; 343.12; 3.12.12]	[(3342)2; 334.12; 343.12; 44]	[33434; 3262; (3446)2; 44]	[36; (3342)2; 33434; 44]	[346; (3342)2; 33434; 44]
[36; 3342; (3464)2; 3446]	[3342; 3262; 3464; (3446)2]	[33434; 3262; 3464; (3446)2]	[36; 33434; (3446)2; 3636]	[3342; 33434; 3464; (3446)2]
[36; 33434; (3262)2; 3446]	[3342; 3262; (3464)2; 3446]	[33434; 3262; (3464)2; 3446]	[346; 3342; (3464)2; 3446]	[36; (3342)2; 33434; 3464]
[36; (3342)2; 33434; 3464]	[36; 3342; (33434)2; 3464]	[(36)2; 3342; 33434; 3464]	[36; 3342; (33434)2; 3464]	[(36)2; 3342; 33434; 334.12]
[36; 33434; (334.12)2; 343.12]	[(36)2; 346; 3342; 33434]	[(36)2; 346; 3262; 63]	[36; (346)2; 3262; 63]	[(36)2; 346; 3262; 3636]
[36; 346; (3262)2; 3636]	[36; (346)2; 3262; 3636]	[(36)2; 346; 3262; 3636]	[36; 346; 3262; (3636)2]	[36; (346)2; 3262; 3636]
[36; (346)2; 3262; 3636]	[36; (346)2; 3262; 3636]	[36; 346; (3262)2; 3636]	[36; 346; (3262)2; 3636]	[36; 346; 3262; (63)2]
[36; 346; (3262)2; 63]	[346; (3262)2; 3636; 63]	[(346)2; 3262; 3636; 63]	[(36)2; 346; 3262; 63]	[(36)2; 346; 3262; 63]
[36; 346; 3262; (63)2]	[36; 346; 3262; (63)2]	[36; 346; 3262; (63)2]	[36; 346; (3262)2; 63]	[346; (3262)2; 3636; 63]
[346; (3262)2; 3636; 63]	[346; (3262)2; 3636; 63]	[346; 3262; 3636; (63)2]	[346; (3262)2; 3636; 63]	[3342; 3262; 3446; (63)2]
[3342; 3262; 3446; (63)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; (3636)2; 44]	[3262; 3446; (3636)2; 44]
[3342; 3262; 3446; (44)2]	[346; 3342; 3446; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; (3636)2; 44]
[3262; 3446; (3636)2; 44]	[3342; 3262; 3446; (44)2]	[346; 3342; 3446; (44)2]	[346; (3342)2; 3636; 44]	[36; 3342; (3446)2; 3636]
[346; (3342)2; 3446; 3636]	[346; (3342)2; 3446; 3636]	[(36)2; 346; 3446; 3636]	[36; 3342; (3446)2; 3636]	[346; (3342)2; 3446; 3636]
[346; (3342)2; 3446; 3636]	[(36)2; 346; 3446; 3636]	[(36)2; 3342; 3446; 3636]	[36; 3342; 3446; (3636)2]	[346; 3342; (3446)2; 3636]
[36; 346; (3342)2; 3446]	[346; (3342)2; 3262; 3636]	[346; (3342)2; 3262; 3636]	[36; (346)2; 3342; 3446]	[36; (346)2; 3342; 3446]
[36; (346)2; 3342; 3446]	[36; 346; (3342)2; 3262]	[(36)2; 346; 3342; 3636]	[(36)2; 346; 3342; 3636]

5-uniform tilings, 3 vertex types (3:1:1) and (2:2:1)

There are 149 5-uniform tilings, with 60 having 3:1:1 copies, and 89 having 2:2:1 copies.

5-uniform tilings (3:1:1)

[36; 334.12; (46.12)3]	[3464; 3446; (46.12)3]	[36; (334.12)3; 46.12]	[334.12; 343.12; (3.12.12)3]	[36; (33434)3; 343.12]
[3262; 3636; (63)3]	[346; 3262; (63)3]	[36; (3262)3; 63]	[36; (3262)3; 63]	[3262; (3636)3; 63]
[3446; 3636; (44)3]	[3446; 3636; (44)3]	[36; 3342; (44)3]	[36; 3342; (44)3]	[3446; (3636)3; 44]
[3446; (3636)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[(36)3; 3342; 44]
[(36)3; 3342; 44]	[3446; 3636; (44)3]	[3446; 3636; (44)3]	[36; 3342; (44)3]	[36; 3342; (44)3]
[(3342)3; 3262; 3446]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]
[3446; (3636)3; 44]	[3446; (3636)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]
[(36)3; 3342; 44]	[(36)3; 3342; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]
[(3342)3; 3446; 3636]	[(3342)3; 3446; 3636]	[346; (3342)3; 3446]	[(36)3; 346; 3262]	[(36)3; 346; 3262]
[(36)3; 346; 3262]	[346; (3262)3; 3636]	[346; (3262)3; 3636]	[(346)3; 3262; 3636]	[(346)3; 3262; 3636]
[(36)3; 346; 3262]	[(36)3; 346; 3262]	[(346)3; 3262; 3636]	[36; 346; (3636)3]	[36; 346; (3636)3]
[36; 346; (3636)3]	[36; 346; (3636)3]	[(36)3; 346; 3636]	[(36)3; 346; 3636]	[36; (346)3; 3636]

5-uniform tilings (2:2:1)

[(3446)2; (3636)2; 46.12]	[(36)2; (3342)2; 3464]	[(3342)2; 334.12; (3464)2]	[36; (33434)2; (3464)2]	[3342; (33434)2; (3464)2]
[3342; (33434)2; (3464)2]	[3342; (33434)2; (3464)2]	[(33434)2; 343.12; (3464)2]	[36; (3262)2; (63)2]	[(3262)2; (3636)2; 63]
[(36)2; (3342)2; 33434]	[(36)2; 3342; (33434)2]	[346; (3342)2; (33434)2]	[(36)2; 3342; (33434)2]	[(36)2; 3342; (33434)2]
[(3262)2; 3636; (63)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[(3446)2; 3636; (44)2]
[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[36; (3342)2; (44)2]	[(36)2; 3342; (44)2]	[(36)2; 3342; (44)2]
[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]
[36; (3342)2; (44)2]	[(36)2; (3342)2; 44]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]
[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[36; (3342)2; (44)2]	[(36)2; 3342; (44)2]
[(36)2; 3342; (44)2]	[36; (3342)2; (44)2]	[36; (3342)2; (44)2]	[(3446)2; 3636; (44)2]	[(36)2; (3342)2; 44]
[(36)2; (3342)2; 44]	[(36)2; (3342)2; 44]	[(36)2; (3342)2; 44]	[(33434)2; 3262; (3446)2]	[3342; (3262)2; (3446)2]
[3342; (3262)2; (3446)2]	[3262; (3446)2; (3636)2]	[(3262)2; 3446; (3636)2]	[(3262)2; 3446; (3636)2]	[(3464)2; (3446)2; 3636]
[3262; (3446)2; (3636)2]	[3262; (3446)2; (3636)2]	[(346)2; (3446)2; 3636]	[(346)2; (3446)2; 3636]	[(346)2; (3446)2; 3636]
[(346)2; (3446)2; 3636]	[(3342)2; (3446)2; 3636]	[(3342)2; (3446)2; 3636]	[(346)2; (3342)2; 3446]	[(346)2; 3342; (3446)2]
[(36)2; (346)2; 3262]	[36; (346)2; (3262)2]	[(36)2; 346; (3262)2]	[(346)2; (3262)2; 63]	[36; (3262)2; (63)2]
[36; (346)2; (3262)2]	[346; (3262)2; (3636)2]	[(346)2; (3262)2; 3636]	[36; (346)2; (3262)2]	[(346)2; 3262; (3636)2]
[(346)2; (3262)2; 3636]	[(36)2; (346)2; 3262]	[(36)2; (346)2; 3262]	[(36)2; (346)2; 3636]	[(36)2; (346)2; 3636]
[36; (346)2; (3342)2]	[(36)2; (346)2; 3262]	[36; (346)2; (3262)2]	[36; (346)2; (3262)2]	[346; (3342)2; (3636)2]
[346; (3342)2; (3636)2]	[(36)2; 346; (3636)2]	[(36)2; (346)2; 3636]	[(36)2; 3342; (33434)2]

5-uniform tilings, 2 vertex types (4:1) and (3:2)

There are 74 5-uniform tilings with 2 types of vertices, 27 with 4:1 and 47 with 3:2 copies of each.

5-uniform tilings (4:1)

[(3464)4; 46.12]	[343.12; (3.12.12)4]	[36; (33434)4]	[36; (33434)4]	[(36)4; 346]
[(36)4; 346]	[(36)4; 346]	[36; (346)4]	[3262; (3636)4]	[(346)4; 3262]
[(346)4; 3262]	[(346)4; 3636]	[3262; (3636)4]	[3446; (3636)4]	[3446; (3636)4]
[(3342)4; 33434]	[3342; (33434)4]
[3342; (44)4]	[3342; (44)4]	[(3342)4; 44]	[(3342)4; 44]	[(3342)4; 44]
[36; (3342)4]	[36; (3342)4]	[36; (3342)4]	[(36)4; 3342]	[(36)4; 3342]

There are 29 5-uniform tilings with 3 and 2 unique vertex figure types.

5-uniform tilings (3:2)

[(3464)2; (46.12)3]	[(3464)2; (46.12)3]	[(3464)3; (3446)2]	[(33434)2; (3464)3]	[(33434)3; (3464)2]
[(36)2; (346)3]	[(36)2; (346)3]	[(36)3; (346)2]	[(36)3; (346)2]	[(36)3; (346)2]
[(36)3; (346)2]	[(36)2; (346)3]	[(36)2; (346)3]	[(36)2; (346)3]
[(3262)2; (3636)3]	[(346)3; (3636)2]	[(346)3; (3636)2]	[(346)2; (3636)3]
[(3446)3; (3636)2]	[(3446)2; (3636)3]	[(3446)3; (3636)2]	[(3446)2; (3636)3]	[(3446)2; (3636)3]
[(3342)3; (33434)2]	[(3342)3; (33434)2]	[(3342)2; (33434)3]	[(3342)2; (33434)3]
[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)3; (44)2]	[(3342)2; (44)3]
[(3342)3; (44)2]	[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)3; (44)2]	[(3342)3; (44)2]
[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)3; (3342)2]
[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]

Higher k-uniform tilings

k-uniform tilings have been enumerated up to 6. There are 673 6-uniform tilings of the Euclidean plane. Brian Galebach's search reproduced Krotenheerdt's list of 10 6-uniform tilings with 6 distinct vertex types, as well as finding 92 of them with 5 vertex types, 187 of them with 4 vertex types, 284 of them with 3 vertex types, and 100 with 2 vertex types.

References

1. k-uniform tilings by regular polygons Archived 2015-06-30 at the Wayback Machine Nils Lenngren, 2009
2. "n-Uniform Tilings". probabilitysports.com. Retrieved 2019-06-21.
3. Critchlow, p.60-61
4. Critchlow, p.62-67
5. Tilings and Patterns, Grünbaum and Shephard 1986, pp. 65-67
6. "In Search of Demiregular Tilings" (PDF). Archived from the original (PDF) on 2016-05-07. Retrieved 2015-06-04.

• Grünbaum, Branko; Shephard, Geoffrey C. (1977). "Tilings by regular polygons". Math. Mag. 50 (5): 227–247. doi:10.2307/2689529. JSTOR 2689529.
• Grünbaum, Branko; Shephard, G. C. (1978). "The ninety-one types of isogonal tilings in the plane". Trans. Am. Math. Soc. 252: 335–353. doi:10.1090/S0002-9947-1978-0496813-3. MR 0496813.
• Debroey, I.; Landuyt, F. (1981). "Equitransitive edge-to-edge tilings". Geometriae Dedicata. 11 (1): 47–60. doi:10.1007/BF00183189. S2CID 122636363.
• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1.
• Ren, Ding; Reay, John R. (1987). "The boundary characteristic and Pick's theorem in the Archimedean planar tilings". Journal of Combinatorial Theory. Series A. 44 (1): 110–119. doi:10.1016/0097-3165(87)90063-X.
• Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
• Order in Space: A design source book, Keith Critchlow, 1970 ISBN 978-0-670-52830-1
• Sommerville, Duncan MacLaren Young (1958). An Introduction to the Geometry of n Dimensions. Dover Publications. Chapter X: The Regular Polytopes
• Préa, P. (1997). "Distance sequences and percolation thresholds in Archimedean Tilings". Mathl. Comput. Modelling. 26 (8–10): 317–320. doi:10.1016/S0895-7177(97)00216-1.
• Kovic, Jurij (2011). "Symmetry-type graphs of Platonic and Archimedean solids". Math. Commun. 16 (2): 491–507.
• Pellicer, Daniel; Williams, Gordon (2012). "Minimal Covers of the Archimedean Tilings, Part 1". The Electronic Journal of Combinatorics. 19 (3): #P6. doi:10.37236/2512.
• Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN 978-0866514613, pp. 50–57

External links

Euclidean and general tiling links:

• n-uniform tilings, Brian Galebach
• Dutch, Steve. "Uniform Tilings". Archived from the original on 2006-09-09. Retrieved 2006-09-09.
• Mitchell, K. "Semi-Regular Tilings". Retrieved 2006-09-09.
• Weisstein, Eric W. "Tessellation". MathWorld.
• Weisstein, Eric W. "Semiregular tessellation". MathWorld.
• Weisstein, Eric W. "Demiregular tessellation". MathWorld.