Fokker–Planck equation

In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well.^[1] The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc.

A solution to the one-dimensional Fokker–Planck equation, with both the drift and the diffusion term. In this case the initial condition is a Dirac delta function centered away from zero velocity. Over time the distribution widens due to random impulses.

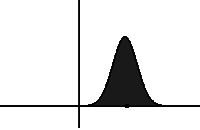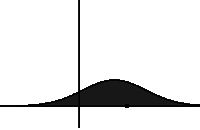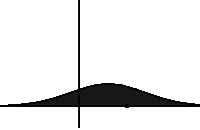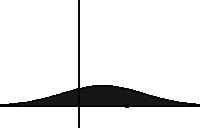
It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917.^[2][3] It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931.^[4] When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski),^[5] and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kramers equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion.^[6]

The first consistent microscopic derivation of the Fokker–Planck equation in the single scheme of classical and quantum mechanics was performed by Nikolay Bogoliubov and Nikolay Krylov.^[7][8]

One dimension

In one spatial dimension x, for an Itô process driven by the standard Wiener process ${\displaystyle W_{t}}$ and described by the stochastic differential equation (SDE) $${\displaystyle dX_{t}=\mu (X_{t},t)\,dt+\sigma (X_{t},t)\,dW_{t}}$$

with drift ${\displaystyle \mu (X_{t},t)}$ and diffusion coefficient ${\displaystyle D(X_{t},t)=\sigma ^{2}(X_{t},t)/2}$, the Fokker–Planck equation for the probability density ${\displaystyle p(x,t)}$ of the random variable ${\displaystyle X_{t}}$ is ^[9]

${\displaystyle {\frac {\partial }{\partial t}}p(x,t)=-{\frac {\partial }{\partial x}}\left[\mu (x,t)p(x,t)\right]+{\frac {\partial ^{2}}{\partial x^{2}}}\left[D(x,t)p(x,t)\right].}$

Link between the Itô SDE and the Fokker–Planck equation

In the following, use ${\displaystyle \sigma ={\sqrt {2D}}}$.

Define the infinitesimal generator ${\displaystyle {\mathcal {L}}}$ (the following can be found in Ref.^[10]): $${\displaystyle {\mathcal {L}}p(X_{t})=\lim _{\Delta t\to 0}{\frac {1}{\Delta t}}\left(\mathbb {E} {\big [}p(X_{t+\Delta t})\mid X_{t}=x{\big ]}-p(x)\right).}$$

The transition probability ${\displaystyle \mathbb {P} _{t,t'}(x\mid x')}$, the probability of going from ${\displaystyle (t',x')}$ to ${\displaystyle (t,x)}$, is introduced here; the expectation can be written as $${\displaystyle \mathbb {E} (p(X_{t+\Delta t})\mid X_{t}=x)=\int p(y)\,\mathbb {P} _{t+\Delta t,t}(y\mid x)\,dy.}$$ Now we replace in the definition of ${\displaystyle {\mathcal {L}}}$, multiply by ${\displaystyle \mathbb {P} _{t,t'}(x\mid x')}$ and integrate over ${\displaystyle dx}$. The limit is taken on $${\displaystyle \int p(y)\int \mathbb {P} _{t+\Delta t,t}(y\mid x)\,\mathbb {P} _{t,t'}(x\mid x')\,dx\,dy-\int p(x)\,\mathbb {P} _{t,t'}(x\mid x')\,dx.}$$ Note now that $${\displaystyle \int \mathbb {P} _{t+\Delta t,t}(y\mid x)\,\mathbb {P} _{t,t'}(x\mid x')\,dx=\mathbb {P} _{t+\Delta t,t'}(y\mid x'),}$$ which is the Chapman–Kolmogorov theorem. Changing the dummy variable ${\displaystyle y}$ to ${\displaystyle x}$, one gets $${\displaystyle {\begin{aligned}\int p(x)\lim _{\Delta t\to 0}{\frac {1}{\Delta t}}\left(\mathbb {P} _{t+\Delta t,t'}(x\mid x')-\mathbb {P} _{t,t'}(x\mid x')\right)\,dx,\end{aligned}}}$$ which is a time derivative. Finally we arrive to $${\displaystyle \int [{\mathcal {L}}p(x)]\mathbb {P} _{t,t'}(x\mid x')\,dx=\int p(x)\,\partial _{t}\mathbb {P} _{t,t'}(x\mid x')\,dx.}$$ From here, the Kolmogorov backward equation can be deduced. If we instead use the adjoint operator of ${\displaystyle {\mathcal {L}}}$, ${\displaystyle {\mathcal {L}}^{\dagger }}$, defined such that $${\displaystyle \int [{\mathcal {L}}p(x)]\mathbb {P} _{t,t'}(x\mid x')\,dx=\int p(x)[{\mathcal {L}}^{\dagger }\mathbb {P} _{t,t'}(x\mid x')]\,dx,}$$ then we arrive to the Kolmogorov forward equation, or Fokker–Planck equation, which, simplifying the notation ${\displaystyle p(x,t)=\mathbb {P} _{t,t'}(x\mid x')}$, in its differential form reads $${\displaystyle {\mathcal {L}}^{\dagger }p(x,t)=\partial _{t}p(x,t).}$$

Remains the issue of defining explicitly ${\displaystyle {\mathcal {L}}}$. This can be done taking the expectation from the integral form of the Itô's lemma: $${\displaystyle \mathbb {E} {\big (}p(X_{t}){\big )}=p(X_{0})+\mathbb {E} \left(\int _{0}^{t}\left(\partial _{t}+\mu \partial _{x}+{\frac {\sigma ^{2}}{2}}\partial _{x}^{2}\right)p(X_{t'})\,dt'\right).}$$

The part that depends on ${\displaystyle dW_{t}}$ vanished because of the martingale property.

Then, for a particle subject to an Itô equation, using $${\displaystyle {\mathcal {L}}=\mu \partial _{x}+{\frac {\sigma ^{2}}{2}}\partial _{x}^{2},}$$ it can be easily calculated, using integration by parts, that $${\displaystyle {\mathcal {L}}^{\dagger }=-\partial _{x}(\mu \cdot )+{\frac {1}{2}}\partial _{x}^{2}(\sigma ^{2}\cdot ),}$$ which bring us to the Fokker–Planck equation: $${\displaystyle \partial _{t}p(x,t)=-\partial _{x}{\big (}\mu (x,t)\cdot p(x,t){\big )}+\partial _{x}^{2}\left({\frac {\sigma (x,t)^{2}}{2}}\,p(x,t)\right).}$$

While the Fokker–Planck equation is used with problems where the initial distribution is known, if the problem is to know the distribution at previous times, the Feynman–Kac formula can be used, which is a consequence of the Kolmogorov backward equation.

The stochastic process defined above in the Itô sense can be rewritten within the Stratonovich convention as a Stratonovich SDE: $${\displaystyle dX_{t}=\left[\mu (X_{t},t)-{\frac {1}{2}}{\frac {\partial }{\partial X_{t}}}D(X_{t},t)\right]\,dt+{\sqrt {2D(X_{t},t)}}\circ dW_{t}.}$$ It includes an added noise-induced drift term due to diffusion gradient effects if the noise is state-dependent. This convention is more often used in physical applications. Indeed, it is well known that any solution to the Stratonovich SDE is a solution to the Itô SDE.

The zero-drift equation with constant diffusion can be considered as a model of classical Brownian motion: $${\displaystyle {\frac {\partial }{\partial t}}p(x,t)=D_{0}{\frac {\partial ^{2}}{\partial x^{2}}}\left[p(x,t)\right].}$$

This model has discrete spectrum of solutions if the condition of fixed boundaries is added for ${\displaystyle \{0\leq x\leq L\}}$: $${\displaystyle {\begin{aligned}p(0,t)&=p(L,t)=0,\\p(x,0)&=p_{0}(x).\end{aligned}}}$$

It has been shown^[11] that in this case an analytical spectrum of solutions allows deriving a local uncertainty relation for the coordinate-velocity phase volume: $${\displaystyle \Delta x\,\Delta v\geq D_{0}.}$$ Here ${\displaystyle D_{0}}$ is a minimal value of a corresponding diffusion spectrum ${\displaystyle D_{j}}$, while ${\displaystyle \Delta x}$ and ${\displaystyle \Delta v}$ represent the uncertainty of coordinate–velocity definition.

Higher dimensions

More generally, if

$${\displaystyle d\mathbf {X} _{t}={\boldsymbol {\mu }}(\mathbf {X} _{t},t)\,dt+{\boldsymbol {\sigma }}(\mathbf {X} _{t},t)\,d\mathbf {W} _{t},}$$

where ${\displaystyle \mathbf {X} _{t}}$ and ${\displaystyle {\boldsymbol {\mu }}(\mathbf {X} _{t},t)}$ are N-dimensional vectors, ${\displaystyle {\boldsymbol {\sigma }}(\mathbf {X} _{t},t)}$ is an ${\displaystyle N\times M}$ matrix and ${\displaystyle \mathbf {W} _{t}}$ is an M-dimensional standard Wiener process, the probability density ${\displaystyle p(\mathbf {x} ,t)}$ for ${\displaystyle \mathbf {X} _{t}}$ satisfies the Fokker–Planck equation

${\displaystyle {\frac {\partial p(\mathbf {x} ,t)}{\partial t}}=-\sum _{i=1}^{N}{\frac {\partial }{\partial x_{i}}}\left[\mu _{i}(\mathbf {x} ,t)p(\mathbf {x} ,t)\right]+\sum _{i=1}^{N}\sum _{j=1}^{N}{\frac {\partial ^{2}}{\partial x_{i}\,\partial x_{j}}}\left[D_{ij}(\mathbf {x} ,t)p(\mathbf {x} ,t)\right],}$

with drift vector ${\displaystyle {\boldsymbol {\mu }}=(\mu _{1},\ldots ,\mu _{N})}$ and diffusion tensor ${\textstyle \mathbf {D} ={\frac {1}{2}}{\boldsymbol {\sigma \sigma }}^{\mathsf {T}}}$, i.e.$${\displaystyle D_{ij}(\mathbf {x} ,t)={\frac {1}{2}}\sum _{k=1}^{M}\sigma _{ik}(\mathbf {x} ,t)\sigma _{jk}(\mathbf {x} ,t).}$$

If instead of an Itô SDE, a Stratonovich SDE is considered,

$${\displaystyle d\mathbf {X} _{t}={\boldsymbol {\mu }}(\mathbf {X} _{t},t)\,dt+{\boldsymbol {\sigma }}(\mathbf {X} _{t},t)\circ d\mathbf {W} _{t},}$$

the Fokker–Planck equation will read:^[10]: 129

$${\displaystyle {\frac {\partial p(\mathbf {x} ,t)}{\partial t}}=-\sum _{i=1}^{N}{\frac {\partial }{\partial x_{i}}}\left[\mu _{i}(\mathbf {x} ,t)\,p(\mathbf {x} ,t)\right]+{\frac {1}{2}}\sum _{k=1}^{M}\sum _{i=1}^{N}{\frac {\partial }{\partial x_{i}}}\left\{\sigma _{ik}(\mathbf {x} ,t)\sum _{j=1}^{N}{\frac {\partial }{\partial x_{j}}}\left[\sigma _{jk}(\mathbf {x} ,t)\,p(\mathbf {x} ,t)\right]\right\}}$$

Analytical Theory of Mean First Passage Time

In the theory of stochastic processes, the mean first passage time (MFPT) is the expected time for a stochastic trajectory to reach a specified boundary or target region for the first time. For a diffusion process governed by the stochastic differential equation (SDE)

${\displaystyle dX_{t}=b(X_{t}),dt+{\sqrt {2\varepsilon }},\sigma (X_{t}),dW_{t},}$

the evolution of the probability density ${\displaystyle p(x,t)}$ is described by the Fokker–Planck equation:

${\displaystyle {\frac {\partial p}{\partial t}}=-\nabla \cdot (b(x)p)+\varepsilon \nabla \cdot \left(D(x)\nabla p\right),}$ where ${\displaystyle D(x)=\sigma (x)\sigma (x)^{T}}$ is the diffusion tensor, and ${\displaystyle \varepsilon \ll 1}$ is the noise intensity.

To compute the MFPT ${\displaystyle u(x)=\mathbb {E} _{x}[\tau ]}$, where ${\displaystyle \tau }$ is the first exit time from a domain ${\displaystyle \Omega }$, one solves the backward Kolmogorov equation, also known as the Dynkin equation:

${\displaystyle {\mathcal {L}}u(x)=-1,\quad x\in \Omega$ ;\qquad u(x)=0,\quad x\in \partial \Omega ,} with generator

${\displaystyle {\mathcal {L}}=b(x)\cdot \nabla +\varepsilon \sum _{i,j}D_{ij}(x){\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}.}$

Boundary Layers and WKB Asymptotics

In the small noise regime (${\displaystyle \varepsilon \to 0}$), solutions typically exhibit boundary layers near ${\displaystyle \partial \Omega }$, where escape occurs. The MFPT can be approximated using the WKB (Wentzel–Kramers–Brillouin) ansatz:

${\displaystyle u(x)\sim A(x)\exp \left({\frac {S(x)}{\varepsilon }}\right),}$ where ${\displaystyle S(x)}$ is the quasi-potential or minimum action required for escape, and ${\displaystyle A(x)}$ is a transport coefficient. The function ${\displaystyle S(x)}$ solves a Hamilton–Jacobi equation and represents the most likely escape path under small random perturbations. These techniques were developed in the analytical framework of Zeev Schuss.^[12][13]

In systems with limit cycle attractors, such as those seen in oscillatory biological systems, the exit time distribution deviates from the classical Poisson law, the survival probability ${\displaystyle P(t)}$ of the process decaying from the limit cycle is modulated in time:

${\displaystyle P(t)=\mathbb {P} (\tau >t)\not \sim e^{-\lambda t},}$

Instead, the survival probability contains oscillatory terms reflecting the periodic nature of the attractor. The conditional exit time density ${\displaystyle f(t)}$ is no longer exponential and is better described through an expansion in Hermite polynomials:

${\displaystyle Pr(\tau >t)=\sum _{n=1}^{\infty }c_{n}\exp(-\lambda _{n}t)cos(\omega nt)}$,

where the coefficients ${\displaystyle c_{n}}$ reflect how strongly the exit probability deviates from the exponential form due to phase preference along the limit cycle. This expansion reveals that escape occurs with higher probability at particular phases of the cycle, breaking the memoryless (Markovian) nature of classical escape theory.^[14] The rate of escape depends not only on the noise intensity but also on geometric and dynamical anisotropies along the attractor. This phenomenon is particularly relevant for modeling neuronal excitability, biological clocks, and cardiac rhythms, where timing and variability of transitions are tightly regulated but also susceptible to random perturbations.

Asymptotic MFPT in Gradient Systems

In systems with small noise and a drift given by the gradient of a potential, b(x)=−∇ϕ(x), the stochastic process ${\displaystyle dX_{t}=-\nabla \phi (X_{t})\,dt+{\sqrt {2\varepsilon }}\,dW_{t}}$

models the overdamped Langevin dynamics of a particle in a potential landscape ϕ(x)ϕ(x). The associated mean first passage time u(x)u(x), which satisfies the backward Kolmogorov equation:

${\displaystyle \varepsilon \Delta u(x)-\nabla \phi (x)\cdot \nabla u(x)=-1,}$

subject to u=0 on the exit boundary ∂Ωa⊂∂Ω∂Ωa​⊂∂Ω, has the following asymptotic solution in the limit ε→0, when x is near a local minimum x0 of ϕ and escape occurs over a saddle point xsxs of the potential:

${\displaystyle \mathbb {E} [\tau ]\sim {\frac {2\pi }{\sqrt {|\det H(x_{s})|}}}\cdot {\frac {e^{[\phi (x_{s})-\phi (x_{0})]/\varepsilon }}{\sqrt {\det H(x_{0})}}},}$

where:

   ${\displaystyle H(x_{0})}$ is the Hessian matrix of ϕ at the stable point x0,

   ${\displaystyle H(x_{s})}$ is the Hessian at the saddle point xs, with one negative eigenvalue,

  ϕ(xs)−ϕ(x0) is the energy barrier or quasi-potential difference the system must cross.

This formula generalizes Kramers' escape time to n-dimensional gradient systems and shows the exponential sensitivity of MFPT to potential barriers, with prefactors determined by second-order variations (local curvatures) of the potential at critical points. This result connects with large deviation theory and WKB asymptotics, where the action functional (or quasi-potential) governs the probability of rare events. It underpins modern approaches to metastability in physics, chemistry, and biology—such as chemical reaction rates, ion channel gating, or noise-induced switching in gene networks.

Generalization

In general, the Fokker–Planck equations are a special case to the general Kolmogorov forward equation

$${\displaystyle \partial _{t}\rho ={\mathcal {A}}^{*}\rho }$$

where the linear operator ${\displaystyle {\mathcal {A}}^{*}}$ is the Hermitian adjoint to the infinitesimal generator for the Markov process.^[15]

Examples

Wiener process

A standard scalar Wiener process is generated by the stochastic differential equation

$${\displaystyle dX_{t}=dW_{t}.}$$

Here the drift term is zero and the diffusion coefficient is 1/2. Thus the corresponding Fokker–Planck equation is

$${\displaystyle {\frac {\partial p(x,t)}{\partial t}}={\frac {1}{2}}{\frac {\partial ^{2}p(x,t)}{\partial x^{2}}},}$$

which is the simplest form of a diffusion equation. If the initial condition is ${\displaystyle p(x,0)=\delta (x)}$, the solution is

$${\displaystyle p(x,t)={\frac {1}{\sqrt {2\pi t}}}e^{-{x^{2}}/({2t})}.}$$

Boltzmann distribution at the thermodynamic equilibrium

The overdamped Langevin equation$${\displaystyle dx_{t}=-{\frac {1}{k_{\text{B}}T}}(\nabla _{x}U)dt+dW_{t}}$$gives ${\textstyle \partial _{t}p={\frac {1}{2}}\nabla \cdot \left({\frac {p}{k_{\text{B}}T}}\nabla U+\nabla p\right)}$. The Boltzmann distribution ${\displaystyle p(x)\propto e^{-U(x)/k_{\text{B}}T}}$ is an equilibrium distribution, and assuming ${\displaystyle U}$ grows sufficiently rapidly (that is, the potential well is deep enough to confine the particle), the Boltzmann distribution is the unique equilibrium.

Ornstein–Uhlenbeck process

The Ornstein–Uhlenbeck process is a process defined as

$${\displaystyle dX_{t}=-aX_{t}\,dt+\sigma \,dW_{t}.}$$

with ${\displaystyle a>0}$. Physically, this equation can be motivated as follows: a particle of mass ${\displaystyle m}$ with velocity ${\displaystyle V_{t}}$ moving in a medium, e.g., a fluid, will experience a friction force which resists motion whose magnitude can be approximated as being proportional to particle's velocity ${\displaystyle -aV_{t}}$ with ${\displaystyle a=\mathrm {constant} }$. Other particles in the medium will randomly kick the particle as they collide with it and this effect can be approximated by a white noise term; ${\displaystyle \sigma (dW_{t}/dt)}$. Newton's second law is written as

$${\displaystyle m{\frac {dV_{t}}{dt}}=-aV_{t}+\sigma {\frac {dW_{t}}{dt}}.}$$

Taking ${\displaystyle m=1}$ for simplicity and changing the notation as ${\displaystyle V_{t}\rightarrow X_{t}}$ leads to the familiar form ${\displaystyle dX_{t}=-aX_{t}dt+\sigma dW_{t}}$.

The corresponding Fokker–Planck equation is $${\displaystyle {\frac {\partial p(x,t)}{\partial t}}=a{\frac {\partial }{\partial x}}\left(x\,p(x,t)\right)+{\frac {\sigma ^{2}}{2}}{\frac {\partial ^{2}p(x,t)}{\partial x^{2}}},}$$

The stationary solution (${\displaystyle \partial _{t}p=0}$) is $${\displaystyle p_{ss}(x)={\sqrt {\frac {a}{\pi \sigma ^{2}}}}e^{-{ax^{2}}/{\sigma ^{2}}}.}$$

Plasma physics

In plasma physics, the distribution function for a particle species ${\displaystyle s}$, ${\displaystyle p_{s}(\mathbf {x} ,\mathbf {v} ,t)}$, takes the place of the probability density function. The corresponding Boltzmann equation is given by

$${\displaystyle {\frac {\partial p_{s}}{\partial t}}+\mathbf {v} \cdot {\boldsymbol {\nabla }}p_{s}+{\frac {Z_{s}e}{m_{s}}}\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot {\boldsymbol {\nabla }}_{v}p_{s}=-{\frac {\partial }{\partial v_{i}}}\left(p_{s}\langle \Delta v_{i}\rangle \right)+{\frac {1}{2}}{\frac {\partial ^{2}}{\partial v_{i}\,\partial v_{j}}}\left(p_{s}\langle \Delta v_{i}\,\Delta v_{j}\rangle \right),}$$

where the third term includes the particle acceleration due to the Lorentz force and the Fokker–Planck term at the right-hand side represents the effects of particle collisions. The quantities ${\displaystyle \langle \Delta v_{i}\rangle }$ and ${\displaystyle \langle \Delta v_{i}\,\Delta v_{j}\rangle }$ are the average change in velocity a particle of type ${\displaystyle s}$ experiences due to collisions with all other particle species in unit time. Expressions for these quantities are given elsewhere.^[16] If collisions are ignored, the Boltzmann equation reduces to the Vlasov equation.

Smoluchowski diffusion equation

Consider an overdamped Brownian particle under external force ${\displaystyle F(r)}$:^[17]$${\displaystyle m{\ddot {r}}=-\gamma {\dot {r}}+F(r)+\sigma \xi (t)}$$where the ${\displaystyle m{\ddot {r}}}$ term is negligible (the meaning of "overdamped"). Thus, it is just ${\displaystyle \gamma \,dr=F(r)\,dt+\sigma \,dW_{t}}$. The Fokker–Planck equation for this particle is the Smoluchowski diffusion equation: $${\displaystyle \partial _{t}P(r,t|r_{0},t_{0})=\nabla \cdot [D(\nabla -\beta F(r))P(r,t|r_{0},t_{0})]}$$Where ${\displaystyle D}$ is the diffusion constant and ${\displaystyle \beta ={\frac {1}{k_{\text{B}}T}}}$. The importance of this equation is it allows for both the inclusion of the effect of temperature on the system of particles and a spatially dependent diffusion constant.

Derivation of the Smoluchowski Equation from the Fokker–Planck Equation

Starting with the Langevin Equation of a Brownian particle in external field ${\displaystyle F(r)}$, where ${\displaystyle \gamma }$ is the friction term, ${\displaystyle \xi }$ is a fluctuating force on the particle, and ${\displaystyle \sigma }$ is the amplitude of the fluctuation.

$${\displaystyle m{\ddot {r}}=-\gamma {\dot {r}}+F(r)+\sigma \xi (t)}$$

At equilibrium the frictional force is much greater than the inertial force, ${\displaystyle \left\vert \gamma {\dot {r}}\right\vert \gg \left\vert m{\ddot {r}}\right\vert }$. Therefore, the Langevin equation becomes,

$${\displaystyle \gamma {\dot {r}}=F(r)+\sigma \xi (t)}$$

Which generates the following Fokker–Planck equation,

$${\displaystyle \partial _{t}P(r,t|r_{0},t_{0})=\left(\nabla ^{2}{\frac {\sigma ^{2}}{2\gamma ^{2}}}-\nabla \cdot {\frac {F(r)}{\gamma }}\right)P(r,t|r_{0},t_{0})}$$

Rearranging the Fokker–Planck equation,

$${\displaystyle \partial _{t}P(r,t|r_{0},t_{0})=\nabla \cdot \left(\nabla D-{\frac {F(r)}{\gamma }}\right)P(r,t|r_{0},t_{0})}$$

Where ${\displaystyle D={\frac {\sigma ^{2}}{2\gamma ^{2}}}}$. Note, the diffusion coefficient may not necessarily be spatially independent if ${\displaystyle \sigma }$ or ${\displaystyle \gamma }$ are spatially dependent.

Next, the total number of particles in any particular volume is given by,

$${\displaystyle N_{V}(t|r_{0},t_{0})=\int _{V}drP(r,t|r_{0},t_{0})}$$

Therefore, the flux of particles can be determined by taking the time derivative of the number of particles in a given volume, plugging in the Fokker–Planck equation, and then applying Gauss's Theorem.

$${\displaystyle \partial _{t}N_{V}(t|r_{0},t_{0})=\int _{V}dV\nabla \cdot \left(\nabla D-{\frac {F(r)}{\gamma }}\right)P(r,t|r_{0},t_{0})=\int _{\partial V}d\mathbf {a} \cdot j(r,t|r_{0},t_{0})}$$

$${\displaystyle j(r,t|r_{0},t_{0})=\left(\nabla D-{\frac {F(r)}{\gamma }}\right)P(r,t|r_{0},t_{0})}$$

In equilibrium, it is assumed that the flux goes to zero. Therefore, Boltzmann statistics can be applied for the probability of a particles location at equilibrium, where ${\displaystyle F(r)=-\nabla U(r)}$ is a conservative force and the probability of a particle being in a state ${\displaystyle r}$ is given as ${\displaystyle P(r,t|r_{0},t_{0})={\frac {e^{-\beta U(r)}}{Z}}}$.

$${\displaystyle j(r,t|r_{0},t_{0})=\left(\nabla D-{\frac {F(r)}{\gamma }}\right){\frac {e^{-\beta U(r)}}{Z}}=0}$$

$${\displaystyle \Rightarrow \nabla D=F(r)\left({\frac {1}{\gamma }}-D\beta \right)}$$

This relation is a realization of the fluctuation–dissipation theorem. Now applying ${\displaystyle \nabla \cdot \nabla }$ to ${\displaystyle DP(r,t|r_{0},t_{0})}$ and using the Fluctuation-dissipation theorem,

$${\displaystyle {\begin{aligned}\nabla \cdot \nabla DP(r,t|r_{0},t_{0})&=\nabla \cdot D\nabla P(r,t|r_{0},t_{0})+\nabla \cdot P(r,t|r_{0},t_{0})\nabla D\\&=\nabla \cdot D\nabla P(r,t|r_{0},t_{0})+\nabla \cdot P(r,t|r_{0},t_{0}){\frac {F(r)}{\gamma }}-\nabla \cdot P(r,t|r_{0},t_{0})D\beta F(r)\end{aligned}}}$$

Rearranging,

$${\displaystyle \Rightarrow \nabla \cdot \left(\nabla D-{\frac {F(r)}{\gamma }}\right)P(r,t|r_{0},t_{0})=\nabla \cdot D(\nabla -\beta F(r))P(r,t|r_{0},t_{0})}$$

Therefore, the Fokker–Planck equation becomes the Smoluchowski equation, $${\displaystyle \partial _{t}P(r,t|r_{0},t_{0})=\nabla \cdot D(\nabla -\beta F(r))P(r,t|r_{0},t_{0})}$$

for an arbitrary force ${\displaystyle F(r)}$.

Computational considerations

Brownian motion follows the Langevin equation, which can be solved for many different stochastic forcings with results being averaged (canonical ensemble in molecular dynamics). However, instead of this computationally intensive approach, one can use the Fokker–Planck equation and consider the probability ${\displaystyle p(\mathbf {v} ,t)\,d\mathbf {v} }$ of the particle having a velocity in the interval ${\displaystyle (\mathbf {v} ,\mathbf {v} +d\mathbf {v} )}$ when it starts its motion with ${\displaystyle \mathbf {v} _{0}}$ at time 0.

Brownian dynamics simulation for particles in 1-D linear potential compared with the solution of the Fokker–Planck equation

1-D linear potential example

Brownian dynamics in one dimension is simple.^[17][18]

Theory

Starting with a linear potential of the form ${\displaystyle U(x)=cx}$ the corresponding Smoluchowski equation becomes,

$${\displaystyle \partial _{t}P(x,t|x_{0},t_{0})=\partial _{x}D(\partial _{x}+\beta c)P(x,t|x_{0},t_{0})}$$

Where the diffusion constant, ${\displaystyle D}$, is constant over space and time. The boundary conditions are such that the probability vanishes at ${\displaystyle x\rightarrow \pm \infty }$ with an initial condition of the ensemble of particles starting in the same place, ${\displaystyle P(x,t=t_{0}|x_{0},t_{0})=\delta (x-x_{0})}$.

Defining ${\displaystyle \tau =Dt}$ and ${\displaystyle b=\beta c}$ and applying the coordinate transformation,

$${\displaystyle y=x+\tau b,\ \ \ y_{0}=x_{0}+\tau _{0}b}$$

With ${\displaystyle P(x,t,|x_{0},t_{0})=q(y,\tau |y_{0},\tau _{0})}$ the Smoluchowki equation becomes, $${\displaystyle \partial _{\tau }q(y,\tau |y_{0},\tau _{0})=\partial _{y}^{2}q(y,\tau |y_{0},\tau _{0})}$$

Which is the free diffusion equation with solution, $${\displaystyle q(y,\tau |y_{0},\tau _{0})={\frac {1}{\sqrt {4\pi (\tau -\tau _{0})}}}e^{-{\frac {(y-y_{0})^{2}}{4(\tau -\tau _{0})}}}}$$

And after transforming back to the original coordinates, $${\displaystyle P(x,t|x_{0},t_{0})={\frac {1}{\sqrt {4\pi D(t-t_{0})}}}\exp {\left[{-{\frac {(x-x_{0}+D\beta c(t-t_{0}))^{2}}{4D(t-t_{0})}}}\right]}}$$

Simulation

The simulation on the right was completed using a Brownian dynamics simulation.^[19][20] Starting with a Langevin equation for the system, $${\displaystyle m{\ddot {x}}=-\gamma {\dot {x}}-c+\sigma \xi (t)}$$ where ${\displaystyle \gamma }$ is the friction term, ${\displaystyle \xi }$ is a fluctuating force on the particle, and ${\displaystyle \sigma }$ is the amplitude of the fluctuation. At equilibrium the frictional force is much greater than the inertial force, ${\displaystyle \left|\gamma {\dot {x}}\right|\gg \left|m{\ddot {x}}\right|}$. Therefore, the Langevin equation becomes, $${\displaystyle \gamma {\dot {x}}=-c+\sigma \xi (t)}$$

For the Brownian dynamic simulation the fluctuation force ${\displaystyle \xi (t)}$ is assumed to be Gaussian with the amplitude being dependent of the temperature of the system ${\textstyle \sigma ={\sqrt {2\gamma k_{\text{B}}T}}}$. Rewriting the Langevin equation,

$${\displaystyle {\frac {dx}{dt}}=-D\beta c+{\sqrt {2D}}\xi (t)}$$ where ${\textstyle D={\frac {k_{\text{B}}T}{\gamma }}}$ is the Einstein relation. The integration of this equation was done using the Euler–Maruyama method to numerically approximate the path of this Brownian particle.

Solution

Being a partial differential equation, the Fokker–Planck equation can be solved analytically only in special cases. A formal analogy of the Fokker–Planck equation with the Schrödinger equation allows the use of advanced operator techniques known from quantum mechanics for its solution in a number of cases. Furthermore, in the case of overdamped dynamics when the Fokker–Planck equation contains second partial derivatives with respect to all spatial variables, the equation can be written in the form of a master equation that can easily be solved numerically.^[21] In many applications, one is only interested in the steady-state probability distribution ${\displaystyle p_{0}(x)}$, which can be found from ${\textstyle {\frac {\partial p(x,t)}{\partial t}}=0}$. The computation of mean first passage times and splitting probabilities can be reduced to the solution of an ordinary differential equation which is intimately related to the Fokker–Planck equation.

Particular cases with known solution and inversion

In mathematical finance for volatility smile modeling of options via local volatility, one has the problem of deriving a diffusion coefficient ${\displaystyle {\sigma }(\mathbf {X} _{t},t)}$ consistent with a probability density obtained from market option quotes. The problem is therefore an inversion of the Fokker–Planck equation: Given the density f(x,t) of the option underlying X deduced from the option market, one aims at finding the local volatility ${\displaystyle {\sigma }(\mathbf {X} _{t},t)}$ consistent with f. This is an inverse problem that has been solved in general by Dupire (1994, 1997) with a non-parametric solution.^[22][23] Brigo and Mercurio (2002, 2003) propose a solution in parametric form via a particular local volatility ${\displaystyle {\sigma }(\mathbf {X} _{t},t)}$ consistent with a solution of the Fokker–Planck equation given by a mixture model.^[24][25] More information is available also in Fengler (2008),^[26] Gatheral (2008),^[27] and Musiela and Rutkowski (2008).^[28]

Fokker–Planck equation and path integral

Every Fokker–Planck equation is equivalent to a path integral. The path integral formulation is an excellent starting point for the application of field theory methods.^[29] This is used, for instance, in critical dynamics.

A derivation of the path integral is possible in a similar way as in quantum mechanics. The derivation for a Fokker–Planck equation with one variable ${\displaystyle x}$ is as follows. Start by inserting a delta function and then integrating by parts:

$${\displaystyle {\begin{aligned}{\frac {\partial }{\partial t}}p{\left(x',t\right)}&=-{\frac {\partial }{\partial x'}}\left[D_{1}(x',t)p(x',t)\right]+{\frac {\partial ^{2}}{\partial {x'}^{2}}}\left[D_{2}(x',t)p(x',t)\right]\\[1ex]&=\int _{-\infty }^{\infty }dx\left[\left(D_{1}{\left(x,t\right)}{\frac {\partial }{\partial x}}+D_{2}{\left(x,t\right)}{\frac {\partial ^{2}}{\partial x^{2}}}\right)\delta {\left(x'-x\right)}\right]p(x,t).\end{aligned}}}$$

The ${\displaystyle x}$-derivatives here only act on the ${\displaystyle \delta }$-function, not on ${\displaystyle p(x,t)}$. Integrate over a time interval ${\displaystyle \varepsilon }$,

$${\displaystyle p(x',t+\varepsilon )=\int _{-\infty }^{\infty }\,\mathrm {d} x\left(\left(1+\varepsilon \left[D_{1}(x,t){\frac {\partial }{\partial x}}+D_{2}(x,t){\frac {\partial ^{2}}{\partial x^{2}}}\right]\right)\delta (x'-x)\right)p(x,t)+O(\varepsilon ^{2}).}$$

Insert the Fourier integral

$${\displaystyle \delta {\left(x'-x\right)}=\int _{-i\infty }^{i\infty }{\frac {\mathrm {d} {\tilde {x}}}{2\pi i}}e^{{\tilde {x}}{\left(x-x'\right)}}}$$

for the ${\displaystyle \delta }$-function,

$${\displaystyle {\begin{aligned}p(x',t+\varepsilon )&=\int _{-\infty }^{\infty }\mathrm {d} x\int _{-i\infty }^{i\infty }{\frac {\mathrm {d} {\tilde {x}}}{2\pi i}}\left(1+\varepsilon \left[{\tilde {x}}D_{1}(x,t)+{\tilde {x}}^{2}D_{2}(x,t)\right]\right)e^{{\tilde {x}}(x-x')}p(x,t)+O(\varepsilon ^{2})\\[5pt]&=\int _{-\infty }^{\infty }\mathrm {d} x\int _{-i\infty }^{i\infty }{\frac {\mathrm {d} {\tilde {x}}}{2\pi i}}\exp \left(\varepsilon \left[-{\tilde {x}}{\frac {(x'-x)}{\varepsilon }}+{\tilde {x}}D_{1}(x,t)+{\tilde {x}}^{2}D_{2}(x,t)\right]\right)p(x,t)+O(\varepsilon ^{2}).\end{aligned}}}$$

This equation expresses ${\displaystyle p(x',t+\varepsilon )}$ as functional of ${\displaystyle p(x,t)}$. Iterating ${\displaystyle (t'-t)/\varepsilon }$ times and performing the limit ${\displaystyle \varepsilon \rightarrow 0}$ gives a path integral with action

$${\displaystyle S=\int \mathrm {d} t\left[{\tilde {x}}D_{1}(x,t)+{\tilde {x}}^{2}D_{2}(x,t)-{\tilde {x}}{\frac {\partial x}{\partial t}}\right].}$$

The variables ${\displaystyle {\tilde {x}}}$ conjugate to ${\displaystyle x}$ are called "response variables".^[30]

Although formally equivalent, different problems may be solved more easily in the Fokker–Planck equation or the path integral formulation. The equilibrium distribution for instance may be obtained more directly from the Fokker–Planck equation.

See also

• Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy of equations
• Boltzmann equation
• Convection–diffusion equation
• Klein–Kramers equation
• Kolmogorov backward equation
• Kolmogorov equation
• Langevin equation
• Master equation
• Mean-field game theory
• Ornstein–Uhlenbeck process
• Vlasov equation