Coordination complex

A coordination complex is a chemical compound consisting of a central atom or ion, which is usually metallic and is called the coordination centre, and a surrounding array of bound molecules or ions, that are in turn known as ligands or complexing agents.^[1][2][3] Many metal-containing compounds, especially those that include transition metals (elements like titanium that belong to the periodic table's d-block), are coordination complexes.^[4]

Cisplatin, PtCl₂(NH₃)₂, is a coordination complex of platinum(II) with two chloride and two ammonia ligands. It is one of the most successful anticancer drugs.

Nomenclature and terminology

Coordination complexes are so pervasive that their structures and reactions are described in many ways, sometimes confusingly. The atom within a ligand that is bonded to the central metal atom or ion is called the donor atom. In a typical complex, a metal ion is bonded to several donor atoms, which can be the same or different. A polydentate (multiple bonded) ligand is a molecule or ion that bonds to the central atom through several of the ligand's atoms; ligands with 2, 3, 4 or even 6 bonds to the central atom are common. These complexes are called chelate complexes; the formation of such complexes is called chelation, complexation, and coordination.

The central atom or ion, together with all ligands, comprise the coordination sphere.^[5][6] The central atoms or ion and the donor atoms comprise the first coordination sphere.

Coordination refers to the "coordinate covalent bonds" (dipolar bonds) between the ligands and the central atom. Originally, a complex implied a reversible association of molecules, atoms, or ions through such weak chemical bonds. As applied to coordination chemistry, this meaning has evolved. Some metal complexes are formed virtually irreversibly and many are bound together by bonds that are quite strong.^[7][8]

The number of donor atoms attached to the central atom or ion is called the coordination number. The most common coordination numbers are 2, 4, and especially 6. A hydrated ion is one kind of a complex ion (or simply a complex), a species formed between a central metal ion and one or more surrounding ligands, molecules or ions that contain at least one lone pair of electrons.

If all the ligands are monodentate, then the number of donor atoms equals the number of ligands. For example, the cobalt(II) hexahydrate ion or the hexaaquacobalt(II) ion [Co(H₂O)₆]²⁺ is a hydrated-complex ion that consists of six water molecules attached to a metal ion Co. The oxidation state and the coordination number reflect the number of bonds formed between the metal ion and the ligands in the complex ion. However, the coordination number of Pt(en)²⁺
₂ is 4 (rather than 2) since it has two bidentate ligands, which contain four donor atoms in total.

Any donor atom will give a pair of electrons. There are some donor atoms or groups which can offer more than one pair of electrons. Such are called bidentate (offers two pairs of electrons) or polydentate (offers more than two pairs of electrons). In some cases an atom or a group offers a pair of electrons to two similar or different central metal atoms or acceptors—by division of the electron pair—into a three-center two-electron bond. These are called bridging ligands.

History

Alfred Werner

Coordination complexes have been known since the beginning of modern chemistry. Early well-known coordination complexes include dyes such as Prussian blue. Their properties were first well understood in the late 1800s, following the 1869 work of Christian Wilhelm Blomstrand. Blomstrand developed what has come to be known as the complex ion chain theory. In considering metal amine complexes, he theorized that the ammonia molecules compensated for the charge of the ion by forming chains of the type [(NH₃)_X]^X+, where X is the coordination number of the metal ion. He compared his theoretical ammonia chains to hydrocarbons of the form (CH₂)_X.^[9]

Following this theory, Danish scientist Sophus Mads Jørgensen made improvements to it. In his version of the theory, Jørgensen claimed that when a molecule dissociates in a solution there were two possible outcomes: the ions would bind via the ammonia chains Blomstrand had described or the ions would bind directly to the metal.

It was not until 1893 that the most widely accepted version of the theory today was published by Alfred Werner. Werner's work included two important changes to the Blomstrand theory. The first was that Werner described the two possibilities in terms of location in the coordination sphere. He claimed that if the ions were to form a chain, this would occur outside of the coordination sphere while the ions that bound directly to the metal would do so within the coordination sphere.^[10] In one of his most important discoveries however Werner disproved the majority of the chain theory. Werner discovered the spatial arrangements of the ligands that were involved in the formation of the complex hexacoordinate cobalt. His theory allows one to understand the difference between a coordinated ligand and a charge balancing ion in a compound, for example the chloride ion in the cobaltammine chlorides and to explain many of the previously inexplicable isomers.

In 1911, Werner first resolved the coordination complex hexol into optical isomers, overthrowing the theory that only carbon compounds could possess chirality.^[11]

Structures

Structure of hexol

The ions or molecules surrounding the central atom are called ligands. Ligands are classified as L or X (or a combination thereof), depending on how many electrons they provide for the bond between ligand and central atom. L ligands provide two electrons from a lone electron pair, resulting in a coordinate covalent bond. X ligands provide one electron, with the central atom providing the other electron, thus forming a regular covalent bond. The ligands are said to be coordinated to the atom. For alkenes, the pi bonds can coordinate to metal atoms. An example is ethylene in the complex [PtCl₃(C₂H₄)]⁻ (Zeise's salt).

Geometry

In coordination chemistry, a structure is first described by its coordination number, the number of ligands attached to the metal (more specifically, the number of donor atoms). Usually one can count the ligands attached, but sometimes even the counting can become ambiguous. Coordination numbers are normally between two and nine, but large numbers of ligands are not uncommon for the lanthanides and actinides. The number of bonds depends on the size, charge, and electron configuration of the metal ion and the ligands. Metal ions may have more than one coordination number.

Typically the chemistry of transition metal complexes is dominated by interactions between s and p molecular orbitals of the donor-atoms in the ligands and the d orbitals of the metal ions. The s, p, and d orbitals of the metal can accommodate 18 electrons (see 18-Electron rule). The maximum coordination number for a certain metal is thus related to the electronic configuration of the metal ion (to be more specific, the number of empty orbitals) and to the ratio of the size of the ligands and the metal ion. Large metals and small ligands lead to high coordination numbers, e.g. [Mo(CN)₈]⁴⁻. Small metals with large ligands lead to low coordination numbers, e.g. Pt[P(CMe₃)]₂. Due to their large size, lanthanides, actinides, and early transition metals tend to have high coordination numbers.

Most structures follow the points-on-a-sphere pattern (or, as if the central atom were in the middle of a polyhedron where the corners of that shape are the locations of the ligands), where orbital overlap (between ligand and metal orbitals) and ligand-ligand repulsions tend to lead to certain regular geometries. The most observed geometries are listed below, but there are many cases that deviate from a regular geometry, e.g. due to the use of ligands of diverse types (which results in irregular bond lengths; the coordination atoms do not follow a points-on-a-sphere pattern), due to the size of ligands, or due to electronic effects (see, e.g., Jahn–Teller distortion):

• Linear for two-coordination
• Trigonal planar for three-coordination
• Tetrahedral or square planar for four-coordination
• Trigonal bipyramidal for five-coordination
• Octahedral for six-coordination
• Pentagonal bipyramidal for seven-coordination
• Square antiprismatic for eight-coordination
• Tricapped trigonal prismatic for nine-coordination

The idealized descriptions of 5-, 7-, 8-, and 9- coordination are often indistinct geometrically from alternative structures with slightly differing L-M-L (ligand-metal-ligand) angles, e.g. the difference between square pyramidal and trigonal bipyramidal structures.^[12]

• Square pyramidal for five-coordination^[13]
• Capped octahedral or capped trigonal prismatic for seven-coordination^[14]
• Dodecahedral or bicapped trigonal prismatic for eight-coordination^[15]
• Capped square antiprismatic for nine-coordination

To distinguish between the alternative coordinations for five-coordinated complexes, the τ geometry index was invented by Addison et al.^[16] This index depends on angles by the coordination center and changes between 0 for the square pyramidal to 1 for trigonal bipyramidal structures, allowing to classify the cases in between. This system was later extended to four-coordinated complexes by Houser et al.^[17] and also Okuniewski et al.^[18]

In systems with low d electron count, due to special electronic effects such as (second-order) Jahn–Teller stabilization,^[19] certain geometries (in which the coordination atoms do not follow a points-on-a-sphere pattern) are stabilized relative to the other possibilities, e.g. for some compounds the trigonal prismatic geometry is stabilized relative to octahedral structures for six-coordination.

• Bent for two-coordination
• Trigonal pyramidal for three-coordination
• Trigonal prismatic for six-coordination

Isomerism

The arrangement of the ligands is fixed for a given complex, but in some cases it is mutable by a reaction that forms another stable isomer.

There exist many kinds of isomerism in coordination complexes, just as in many other compounds.

Stereoisomerism

Stereoisomerism occurs with the same bonds in distinct orientations. Stereoisomerism can be further classified into:^[20]

Cis–trans isomerism and facial–meridional isomerism

Cis–trans isomerism occurs in octahedral and square planar complexes (but not tetrahedral). When two ligands are adjacent they are said to be cis, when opposite each other, trans. When three identical ligands occupy one face of an octahedron, the isomer is said to be facial, or fac. In a fac isomer, any two identical ligands are adjacent or cis to each other. If these three ligands and the metal ion are in one plane, the isomer is said to be meridional, or mer. A mer isomer can be considered as a combination of a trans and a cis, since it contains both trans and cis pairs of identical ligands.

• 
  cis-[CoCl₂(NH₃)₄]⁺
• 
  trans-[CoCl₂(NH₃)₄]⁺
• 
  fac-[CoCl₃(NH₃)₃]
• 
  mer-[CoCl₃(NH₃)₃]

Optical isomerism

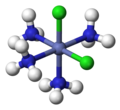
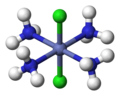
Optical isomerism occurs when a complex is not superimposable with its mirror image. It is so called because the two isomers are each optically active, that is, they rotate the plane of polarized light in opposite directions. In the first molecule shown, the symbol Λ (lambda) is used as a prefix to describe the left-handed propeller twist formed by three bidentate ligands. The second molecule is the mirror image of the first, with the symbol Δ (delta) as a prefix for the right-handed propeller twist. The third and fourth molecules are a similar pair of Λ and Δ isomers, in this case with two bidentate ligands and two identical monodentate ligands.^[21]

• 
  Λ-[Fe(ox)₃]³⁻
• 
  Δ-[Fe(ox)₃]³⁻
• 
  Λ-cis-[CoCl₂(en)₂]⁺
• 
  Δ-cis-[CoCl₂(en)₂]⁺

Structural isomerism

Structural isomerism occurs when the bonds are themselves different. Four types of structural isomerism are recognized: ionisation isomerism, solvate or hydrate isomerism, linkage isomerism and coordination isomerism.

1. Ionisation isomerism – the isomers give different ions in solution although they have the same composition. This type of isomerism occurs when the counter ion of the complex is also a potential ligand. For example, pentaamminebromocobalt(III) sulphate [Co(NH₃)₅Br]SO₄ is red violet and in solution gives a precipitate with barium chloride, confirming the presence of sulphate ion, while pentaamminesulphatecobalt(III) bromide [Co(NH₃)₅SO₄]Br is red and tests negative for sulphate ion in solution, but instead gives a precipitate of AgBr with silver nitrate.^[22]
2. Solvate or hydrate isomerism – the isomers have the same composition but differ with respect to the number of molecules of solvent that serve as ligand vs simply occupying sites in the crystal. Examples: [Cr(H₂O)₆]Cl₃ is violet colored, [CrCl(H₂O)₅]Cl₂·H₂O is blue-green, and [CrCl₂(H₂O)₄]Cl·2H₂O is dark green. See water of crystallization.^[22]
3. Linkage isomerism occurs with ligands with more than one possible donor atom, known as ambidentate ligands.^[23] For example, nitrite can coordinate through O or N.^[24] One pair of nitrite linkage isomers have structures (NH₃)₅CoNO2+2 (nitro isomer) and (NH₃)₅CoONO²⁺ (nitrito isomer).^[23]
4. Coordination isomerism occurs when both positive and negative ions of a salt are complex ions and the two isomers differ in the distribution of ligands between the cation and the anion. For example, [Co(NH₃)₆][Cr(CN)₆] and [Cr(NH₃)₆][Co(CN)₆].^[22]

Electronic properties

Many of the properties of transition metal complexes are dictated by their electronic structures. The electronic structure can be described by a relatively ionic model that ascribes formal charges to the metals and ligands. This approach is the essence of crystal field theory (CFT). Crystal field theory, introduced by Hans Bethe in 1929, gives a quantum mechanically based attempt at understanding complexes. But crystal field theory treats all interactions in a complex as ionic and assumes that the ligands can be approximated by negative point charges.

More sophisticated models embrace covalency, and this approach is described by ligand field theory (LFT) and Molecular orbital theory (MO). Ligand field theory, introduced in 1935 and built from molecular orbital theory, can handle a broader range of complexes and can explain complexes in which the interactions are covalent. The chemical applications of group theory can aid in the understanding of crystal or ligand field theory, by allowing simple, symmetry based solutions to the formal equations.

Chemists tend to employ the simplest model required to predict the properties of interest; for this reason, CFT has been a favorite for the discussions when possible. MO and LF theories are more complicated, but provide a more realistic perspective.

The electronic configuration of the complexes gives them some important properties:

Synthesis of copper(II)-tetraphenylporphyrin, a metal complex, from tetraphenylporphyrin and copper(II) acetate monohydrate.

Color of transition metal complexes

Transition metal complexes often have spectacular colors caused by electronic transitions by the absorption of light. For this reason they are often applied as pigments. Most transitions that are related to colored metal complexes are either d–d transitions or charge transfer bands. In a d–d transition, an electron in a d orbital on the metal is excited by a photon to another d orbital of higher energy, therefore d–d transitions occur only for partially-filled d-orbital complexes (d^1–9). For complexes having d⁰ or d¹⁰ configuration, charge transfer is still possible even though d–d transitions are not. A charge transfer band entails promotion of an electron from a metal-based orbital into an empty ligand-based orbital (metal-to-ligand charge transfer or MLCT). The converse also occurs: excitation of an electron in a ligand-based orbital into an empty metal-based orbital (ligand-to-metal charge transfer or LMCT). These phenomena can be observed with the aid of electronic spectroscopy; also known as UV-Vis.^[25] For simple compounds with high symmetry, the d–d transitions can be assigned using Tanabe–Sugano diagrams. These assignments are gaining increased support with computational chemistry.

Colours of Various Example Coordination Complexes

	Fe2+	Fe3+	Co2+	Cu2+	Al3+	Cr3+
Hydrated Ion	[Fe(H2O)6]2+ Pale green Solution	[Fe(H2O)6]3+ Yellow/brown Solution	[Co(H2O)6]2+ Pink Solution	[Cu(H2O)6]2+ Blue Solution	[Al(H2O)6]3+ Colourless Solution	[Cr(H2O)6]3+ Green Solution
(OH)−, dilute	[Fe(H2O)4(OH)2] Dark green Precipitate	[Fe(H2O)3(OH)3] Brown Precipitate	[Co(H2O)4(OH)2] Blue/green Precipitate	[Cu(H2O)4(OH)2] Blue Precipitate	[Al(H2O)3(OH)3] White Precipitate	[Cr(H2O)3(OH)3] Green Precipitate
(OH)−, concentrated	[Fe(H2O)4(OH)2] Dark green Precipitate	[Fe(H2O)3(OH)3] Brown Precipitate	[Co(H2O)4(OH)2] Blue/green Precipitate	[Cu(H2O)4(OH)2] Blue Precipitate	[Al(OH)4]− Colourless Solution	[Cr(OH)6]3− Green Solution
NH3, dilute	[Fe(NH3)6]2+ Dark green Precipitate	[Fe(NH3)6]3+ Brown Precipitate	[Co(NH3)6]2+ Straw coloured Solution	[Cu(NH3)4(H2O)2]2+ Deep blue Solution	[Al(NH3)3]3+ White Precipitate	[Cr(NH3)6]3+ Purple Solution
NH3, concentrated	[Fe(NH3)6]2+ Dark green Precipitate	[Fe(NH3)6]3+ Brown Precipitate	[Co(NH3)6]2+ Straw coloured Solution	[Cu(NH3)4(H2O)2]2+ Deep blue Solution	[Al(NH3)3]3+ White Precipitate	[Cr(NH3)6]3+ Purple Solution
(CO3)2-	FeCO3 Dark green Precipitate	Fe2(CO3)3 Brown Precipitate+bubbles	CoCO3 Pink Precipitate	CuCO3 Blue/green Precipitate

Colors of lanthanide complexes

Superficially lanthanide complexes are similar to those of the transition metals in that some are colored. However, for the common Ln³⁺ ions (Ln = lanthanide) the colors are all pale, and hardly influenced by the nature of the ligand. The colors are due to 4f electron transitions. As the 4f orbitals in lanthanides are "buried" in the xenon core and shielded from the ligand by the 5s and 5p orbitals they are therefore not influenced by the ligands to any great extent leading to a much smaller crystal field splitting than in the transition metals. The absorption spectra of an Ln³⁺ ion approximates to that of the free ion where the electronic states are described by spin-orbit coupling. This contrasts to the transition metals where the ground state is split by the crystal field. Absorptions for Ln³⁺ are weak as electric dipole transitions are parity forbidden (Laporte forbidden) but can gain intensity due to the effect of a low-symmetry ligand field or mixing with higher electronic states (e.g. d orbitals). f-f absorption bands are extremely sharp which contrasts with those observed for transition metals which generally have broad bands.^[26][27] This can lead to extremely unusual effects, such as significant color changes under different forms of lighting.

Magnetism

Main article: magnetochemistry

Metal complexes that have unpaired electrons are paramagnetic. This can be due to an odd number of electrons overall, or to destabilization of electron-pairing. Thus, monomeric Ti(III) species have one "d-electron" and must be (para)magnetic, regardless of the geometry or the nature of the ligands. Ti(II), with two d-electrons, forms some complexes that have two unpaired electrons and others with none. This effect is illustrated by the compounds TiX₂[(CH₃)₂PCH₂CH₂P(CH₃)₂]₂: when X = Cl, the complex is paramagnetic (high-spin configuration), whereas when X = CH₃, it is diamagnetic (low-spin configuration). Ligands provide an important means of adjusting the ground state properties.

In bi- and polymetallic complexes, in which the individual centres have an odd number of electrons or that are high-spin, the situation is more complicated. If there is interaction (either direct or through ligand) between the two (or more) metal centres, the electrons may couple (antiferromagnetic coupling, resulting in a diamagnetic compound), or they may enhance each other (ferromagnetic coupling). When there is no interaction, the two (or more) individual metal centers behave as if in two separate molecules.

Reactivity

Complexes show a variety of possible reactivities:^[28]

• Electron transfers

  Electron transfer (ET) between metal ions can occur via two distinct mechanisms, inner and outer sphere electron transfers. In an inner sphere reaction, a bridging ligand serves as a conduit for ET.

• (Degenerate) ligand exchange

  One important indicator of reactivity is the rate of degenerate exchange of ligands. For example, the rate of interchange of coordinate water in [M(H₂O)₆]ⁿ⁺ complexes varies over 20 orders of magnitude. Complexes where the ligands are released and rebound rapidly are classified as labile. Such labile complexes can be quite stable thermodynamically. Typical labile metal complexes either have low-charge (Na⁺), electrons in d-orbitals that are antibonding with respect to the ligands (Zn²⁺), or lack covalency (Ln³⁺, where Ln is any lanthanide). The lability of a metal complex also depends on the high-spin vs. low-spin configurations when such is possible. Thus, high-spin Fe(II) and Co(III) form labile complexes, whereas low-spin analogues are inert. Cr(III) can exist only in the low-spin state (quartet), which is inert because of its high formal oxidation state, absence of electrons in orbitals that are M–L antibonding, plus some "ligand field stabilization" associated with the d³ configuration.

• Associative processes

  Complexes that have unfilled or half-filled orbitals are often capable of reacting with substrates. Most substrates have a singlet ground-state; that is, they have lone electron pairs (e.g., water, amines, ethers), so these substrates need an empty orbital to be able to react with a metal centre. Some substrates (e.g., molecular oxygen) have a triplet ground state, which results that metals with half-filled orbitals have a tendency to react with such substrates (it must be said that the dioxygen molecule also has lone pairs, so it is also capable to react as a 'normal' Lewis base).

If the ligands around the metal are carefully chosen, the metal can aid in (stoichiometric or catalytic) transformations of molecules or be used as a sensor.

Classification

Metal complexes, also known as coordination compounds, include virtually all metal compounds.^[29] The study of "coordination chemistry" is the study of "inorganic chemistry" of all alkali and alkaline earth metals, transition metals, lanthanides, actinides, and metalloids. Thus, coordination chemistry is the chemistry of the majority of the periodic table. Metals and metal ions exist, in the condensed phases at least, only surrounded by ligands.

The areas of coordination chemistry can be classified according to the nature of the ligands, in broad terms:

• Classical (or "Werner Complexes"): Ligands in classical coordination chemistry bind to metals, almost exclusively, via their lone pairs of electrons residing on the main-group atoms of the ligand. Typical ligands are H₂O, NH₃, Cl⁻, CN⁻, en. Some of the simplest members of such complexes are described in metal aquo complexes, metal ammine complexes,

Examples: [Co(EDTA)]⁻, [Co(NH₃)₆]³⁺, [Fe(C₂O₄)₃]^3-

• Organometallic chemistry: Ligands are organic (alkenes, alkynes, alkyls) as well as "organic-like" ligands such as phosphines, hydride, and CO.

Example: (C₅H₅)Fe(CO)₂CH₃

• Bioinorganic chemistry: Ligands are those provided by nature, especially including the side chains of amino acids, and many cofactors such as porphyrins.

Example: hemoglobin contains heme, a porphyrin complex of iron

Example: chlorophyll contains a porphyrin complex of magnesium

Many natural ligands are "classical" especially including water.

• Cluster chemistry: Ligands include all of the above as well as other metal ions or atoms as well.

Example Ru₃(CO)₁₂

• In some cases there are combinations of different fields:

Example: [Fe₄S₄(Scysteinyl)₄]²⁻, in which a cluster is embedded in a biologically active species.

Mineralogy, materials science, and solid state chemistry – as they apply to metal ions – are subsets of coordination chemistry in the sense that the metals are surrounded by ligands. In many cases these ligands are oxides or sulfides, but the metals are coordinated nonetheless, and the principles and guidelines discussed below apply. In hydrates, at least some of the ligands are water molecules. It is true that the focus of mineralogy, materials science, and solid state chemistry differs from the usual focus of coordination or inorganic chemistry. The former are concerned primarily with polymeric structures, properties arising from a collective effects of many highly interconnected metals. In contrast, coordination chemistry focuses on reactivity and properties of complexes containing individual metal atoms or small ensembles of metal atoms.

Nomenclature of coordination complexes

The basic procedure for naming a complex is:

1. When naming a complex ion, the ligands are named before the metal ion.
2. The ligands' names are given in alphabetical order. Numerical prefixes do not affect the order.
   • Multiple occurring monodentate ligands receive a prefix according to the number of occurrences: di-, tri-, tetra-, penta-, or hexa-.
   • Multiple occurring polydentate ligands (e.g., ethylenediamine, oxalate) receive bis-, tris-, tetrakis-, etc.
   • Anions end in o. This replaces the final 'e' when the anion ends with '-ide', '-ate' or '-ite', e.g. chloride becomes chlorido and sulfate becomes sulfato. Formerly, '-ide' was changed to '-o' (e.g. chloro and cyano), but this rule has been modified in the 2005 IUPAC recommendations and the correct forms for these ligands are now chlorido and cyanido.^[30]
   • Neutral ligands are given their usual name, with some exceptions: NH₃ becomes ammine; H₂O becomes aqua or aquo; CO becomes carbonyl; NO becomes nitrosyl.
3. Write the name of the central atom/ion. If the complex is an anion, the central atom's name will end in -ate, and its Latin name will be used if available (except for mercury).
4. The oxidation state of the central atom is to be specified (when it is one of several possible, or zero), and should be written as a Roman numeral (or 0) enclosed in parentheses.
5. Name of the cation should be preceded by the name of anion. (if applicable, as in last example)

Examples:

metal	changed to
cobalt	cobaltate
aluminium	aluminate
chromium	chromate
vanadium	vanadate
copper	cuprate
iron	ferrate

[Cd(CN)₂(en)₂] → dicyanidobis(ethylenediamine)cadmium(II)

[CoCl(NH₃)₅]SO₄ → pentaamminechloridocobalt(III) sulfate

[Cu(H₂O)₆] ²⁺ → hexaaquacopper(II) ion

[CuCl₅NH₃]³⁻ → amminepentachloridocuprate(II) ion

K₄[Fe(CN)₆] → potassium hexacyanidoferrate(II)

[NiCl₄]²⁻ → tetrachloridonickelate(II) ion (The use of chloro- was removed from IUPAC naming convention)^[30]

The coordination number of ligands attached to more than one metal (bridging ligands) is indicated by a subscript to the Greek symbol μ placed before the ligand name. Thus the dimer of aluminium trichloride is described by Al₂Cl₄(μ₂-Cl)₂.

Any anionic group can be electronically stabilized by any cation. An anionic complex can be stabilised by a hydrogen cation, becoming an acidic complex which can dissociate to release the cationic hydrogen. This kind of complex compound has a name with "ic" added after the central metal. For example, H₂[Pt(CN)₄] has the name tetracyanoplatinic (II) acid.

Stability constant

Main article: Stability constants of complexes

The affinity of metal ions for ligands is described by a stability constant, also called the formation constant, and is represented by the symbol K_f. It is the equilibrium constant for its assembly from the constituent metal and ligands, and can be calculated accordingly, as in the following example for a simple case:

xM _(aq) + yL _(aq) ⇌ zZ _(aq)

${\displaystyle K_{f}={\frac {[{\text{Z}}]^{z}}{[{\text{M}}]^{x}[{\text{L}}]^{y}}}}$

where : x, y, and z are the stoichiometric coefficients of each species. M stands for metal / metal ion , the L for Lewis bases , and finally Z for complex ions. Formation constants vary widely. Large values indicate that the metal has high affinity for the ligand, provided the system is at equilibrium.^[31]

Sometimes the stability constant will be in a different form known as the constant of destability. This constant is expressed as the inverse of the constant of formation and is denoted as K_d = 1/K_f .^[32] This constant represents the reverse reaction for the decomposition of a complex ion into its individual metal and ligand components. When comparing the values for K_d, the larger the value, the more unstable the complex ion is.

As a result of these complex ions forming in solutions they also can play a key role in solubility of other compounds. When a complex ion is formed it can alter the concentrations of its components in the solution. For example:

Ag⁺
_(aq) + 2 NH₃ ⇌ Ag(NH₃)⁺
₂

AgCl_(s) + H₂O_(l) ⇌ Ag⁺
_(aq) + Cl⁻
_(aq)

If these reactions both occurred in the same reaction vessel, the solubility of the silver chloride would be increased by the presence of NH₄OH because formation of the Diammine argentum(I) complex consumes a significant portion of the free silver ions from the solution. By Le Chatelier's principle, this causes the equilibrium reaction for the dissolving of the silver chloride, which has silver ion as a product, to shift to the right.

This new solubility can be calculated given the values of K_f and K_sp for the original reactions. The solubility is found essentially by combining the two separate equilibria into one combined equilibrium reaction and this combined reaction is the one that determines the new solubility. So K_c, the new solubility constant, is denoted by:

${\displaystyle K_{c}=K_{sp}K_{f}}$

Application of coordination compounds

As metals only exist in solution as coordination complexes, it follows then that this class of compounds is useful in a wide variety of ways.

Bioinorganic chemistry

In bioinorganic chemistry and bioorganometallic chemistry, coordination complexes serve either structural or catalytic functions. An estimated 30% of proteins contain metal ions. Examples include the intensely colored vitamin B₁₂, the heme group in hemoglobin, the cytochromes, the chlorin group in chlorophyll, and carboxypeptidase, a hydrolytic enzyme important in digestion. Another complex ion enzyme is catalase, which decomposes the cell's waste hydrogen peroxide. Synthetic coordination compounds are also used to bind to proteins and especially nucleic acids (e.g. anticancer drug cisplatin).

Industry

Homogeneous catalysis is a major application of coordination compounds for the production of organic substances. Processes include hydrogenation, hydroformylation, oxidation. In one example, a combination of titanium trichloride and triethylaluminium gives rise to Ziegler–Natta catalysts, used for the polymerization of ethylene and propylene to give polymers of great commercial importance as fibers, films, and plastics.

Nickel, cobalt, and copper can be extracted using hydrometallurgical processes involving complex ions. They are extracted from their ores as ammine complexes. Metals can also be separated using the selective precipitation and solubility of complex ions. Cyanide is used chiefly for extraction of gold and silver from their ores.

Phthalocyanine complexes are an important class of pigments.

Analysis

At one time, coordination compounds were used to identify the presence of metals in a sample. Qualitative inorganic analysis has largely been superseded by instrumental methods of analysis such as atomic absorption spectroscopy (AAS), inductively coupled plasma atomic emission spectroscopy (ICP-AES) and inductively coupled plasma mass spectrometry (ICP-MS).

See also

• Activated complex
• IUPAC nomenclature of inorganic chemistry
• Coordination cage
• Coordination geometry
• Coordination isomerism
• Coordination polymers, in which coordination complexes are the repeating units.
• Inclusion compounds
• Organometallic chemistry deals with a special class of coordination compounds where organic fragments are bonded to a metal at least through one C atom.

References

1. Lawrance, Geoffrey A. (2010). Introduction to Coordination Chemistry. Wiley. doi:10.1002/9780470687123. ISBN 9780470687123.
2. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "complex". doi:10.1351/goldbook.C01203
3. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "coordination entity". doi:10.1351/goldbook.C01330
4. Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. ISBN 978-0-08-037941-8.
5. "Definition of coordination sphere". chemistry-dictionary.com.
6. "What Is A Coordination Compound?". Purdue University Department of Chemistry.
7. Cotton, Frank Albert; Geoffrey Wilkinson; Carlos A. Murillo (1999). Advanced Inorganic Chemistry. John Wiley & Sons. p. 1355. ISBN 978-0-471-19957-1.
8. Miessler, Gary L.; Donald Arthur Tarr (1999). Inorganic Chemistry. Prentice Hall. p. 642. ISBN 978-0-13-841891-5.
9. "Coordination compound - History of coordination compounds". Encyclopedia Britannica. Retrieved 2021-07-07.
10. "Coordination Compound".
11. Werner, A. (May 1911). "Zur Kenntnis des asymmetrischen Kobaltatoms. I". Berichte der Deutschen Chemischen Gesellschaft (in German). 44 (2): 1887–1898. doi:10.1002/cber.19110440297.
12. Wells A.F. (1984) Structural Inorganic Chemistry 5th edition Oxford Science Publications ISBN 0-19-855370-6
13. Angelo R. Rossi; Roald. Hoffmann (1975). "Transition metal pentacoordination". Inorganic Chemistry. 14 (2): 365–374. doi:10.1021/ic50144a032.
14. Roald. Hoffmann; Barbara F. Beier; Earl L. Muetterties; Angelo R. Rossi (1977). "Seven-coordination. A molecular orbital exploration of structure, stereochemistry, and reaction dynamics". Inorganic Chemistry. 16 (3): 511–522. doi:10.1021/ic50169a002.
15. Jeremy K. Burdett; Roald Hoffmann; Robert C. Fay (1978). "Eight-Coordination". Inorganic Chemistry. 17 (9): 2553–2568. doi:10.1021/ic50187a041.
16. Addison, A. W.; Rao, N. T.; Reedijk, J.; van Rijn, J.; Verschoor, G. C. (1984). "Synthesis, structure, and spectroscopic properties of copper(II) compounds containing nitrogen–sulphur donor ligands; the crystal and molecular structure of aqua[1,7-bis(N-methylbenzimidazol-2′-yl)-2,6-dithiaheptane]copper(II) perchlorate". J. Chem. Soc., Dalton Trans. (7): 1349–1356. doi:10.1039/dt9840001349.
17. Yang, L.; Powell, D. R.; Houser, R. P. (2007). "Structural variation in copper(I) complexes with pyridylmethylamide ligands: structural analysis with a new four-coordinate geometry index, τ₄". Dalton Trans. (9): 955–64. doi:10.1039/b617136b. PMID 17308676.
18. Okuniewski, A.; Rosiak, D.; Chojnacki, J.; Becker, B. (2015). "Coordination polymers and molecular structures among complexes of mercury(II) halides with selected 1-benzoylthioureas". Polyhedron. 90: 47–57. doi:10.1016/j.poly.2015.01.035.
19. Kaupp, Martin (2001). ""Non-VSEPR" Structures and Bonding in d⁰ Systems". Angew. Chem. Int. Ed. Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#. PMID 11592184.
20. von Zelewsky, A. "Stereochemistry of Coordination Compounds" John Wiley: Chichester, 1995. ISBN 0-471-95599-X.
21. Miessler, Gary L.; Donald Arthur Tarr (1999). "9". Inorganic Chemistry. Prentice Hall. pp. 315, 316. ISBN 978-0-13-841891-5.
22. Huheey, James E., Inorganic Chemistry (3rd ed., Harper & Row 1983), p.524–5 ISBN 0-06-042987-9
23. Jolly, William L. (1984). Modern Inorganic Chemistry. McGraw-Hill. pp. 357–9. ISBN 0-07-032760-2.
24. Huheey, James E., Inorganic Chemistry (3rd ed., Harper & Row 1983), p.513–24 ISBN 0-06-042987-9
25. Harris, D.; Bertolucci, M. (1989). Symmetry and Spectroscopy. Dover Publications. ISBN 9780486661445.
26. Cotton, F. Albert; Wilkinson, Geoffrey; Murillo, Carlos A.; Bochmann, Manfred (1999), Advanced Inorganic Chemistry (6th ed.), New York: Wiley-Interscience, ISBN 0-471-19957-5
27. Cotton, Simon (2006). Lanthanide and Actinide Chemistry. John Wiley & Sons Ltd.
28. R. G. Wilkins Kinetics and Mechanism of Reactions of Transition Metal Complexes, 2nd Edition, VCH, Weinheim, 1991. ISBN 1-56081-125-0
29. Exception: metal vapors, plasmas, and alloys.
30. "Nomenclature of Inorganic Chemistry IUPAC Recommendations 2005" (PDF). IUPAC. section 1.6.4 (p. 10–11). Archived from the original (PDF) on 2014-12-22. Retrieved 2016-03-06.
31. "Complex Ion Equilibria". Archived from the original on 2015-03-08. Retrieved 2015-04-22.
32. Stretton, Tom. "Solubility and Complex-ion Equilibria" (PDF). Archived from the original (PDF) on 2018-09-20. Retrieved 2015-04-22.

Further reading

• De Vito, D.; Weber, J. ; Merbach, A. E. “Calculated Volume and Energy Profiles for Water Exchange on t_2g ⁶ Rhodium(III) and Iridium(III) Hexaaquaions: Conclusive Evidence for an I_a Mechanism” Inorganic Chemistry, 2004, Volume 43, pages 858–863. doi:10.1021/ic035096n
• Zumdahl, Steven S. Chemical Principles, Fifth Edition. New York: Houghton Mifflin, 2005. 943–946, 957. OCLC 77760970
• Harris, D., Bertolucci, M., Symmetry and Spectroscopy. 1989 New York, Dover Publications

External links

• Naming Coordination Compounds
• Transition Metal Complex Colors