F-score

For the significance test, see F-test.

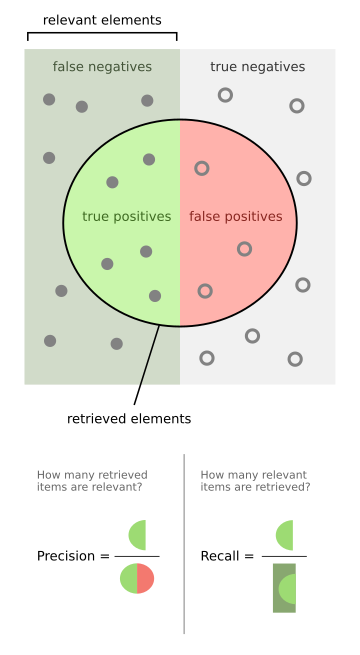
In statistical analysis of binary classification and information retrieval systems, the F-score or F-measure is a measure of predictive performance. It is calculated from the precision and recall of the test, where the precision is the number of true positive results divided by the number of all samples predicted to be positive, including those not identified correctly, and the recall is the number of true positive results divided by the number of all samples that should have been identified as positive. Precision is also known as positive predictive value, and recall is also known as sensitivity in diagnostic binary classification.

Precision and recall

The F₁ score is the harmonic mean of the precision and recall. It thus symmetrically represents both precision and recall in one metric. The more generic ${\displaystyle F_{\beta }}$ score applies additional weights, valuing one of precision or recall more than the other.

The highest possible value of an F-score is 1.0, indicating perfect precision and recall, and the lowest possible value is 0, if precision and recall are zero.

Top Qs

Timeline

Chat

Perspective

Etymology

The name F-measure is believed to be named after a different F function in Van Rijsbergen's book, when introduced to the Fourth Message Understanding Conference (MUC-4, 1992).^[1]

Definition

The traditional F-measure or balanced F-score (F₁ score) is the harmonic mean of precision and recall:^[2]

${\displaystyle F_{1}={\frac {2}{\mathrm {recall} ^{-1}+\mathrm {precision} ^{-1}}}=2{\frac {\mathrm {precision} \cdot \mathrm {recall} }{\mathrm {precision} +\mathrm {recall} }}={\frac {2\mathrm {TP} }{2\mathrm {TP} +\mathrm {FP} +\mathrm {FN} }}}$.

F_β score

A more general F score, ${\displaystyle F_{\beta }}$, that uses a positive real factor ${\displaystyle \beta }$, where ${\displaystyle \beta }$ is chosen such that recall is considered ${\displaystyle \beta }$ times as important as precision, is:

${\displaystyle F_{\beta }=(1+\beta ^{2})\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{(\beta ^{2}\cdot \mathrm {precision} )+\mathrm {recall} }}}$.

In terms of Type I and type II errors this becomes:

${\displaystyle F_{\beta }={\frac {(1+\beta ^{2})\cdot \mathrm {true\ positive} }{(1+\beta ^{2})\cdot \mathrm {true\ positive} +\beta ^{2}\cdot \mathrm {false\ negative} +\mathrm {false\ positive} }}\,}$.

Two commonly used values for ${\displaystyle \beta }$ are 2, which weighs recall higher than precision, and 0.5, which weighs recall lower than precision.

The F-measure was derived so that ${\displaystyle F_{\beta }}$ "measures the effectiveness of retrieval with respect to a user who attaches ${\displaystyle \beta }$ times as much importance to recall as precision".^[3] It is based on Van Rijsbergen's effectiveness measure

${\displaystyle E=1-\left({\frac {\alpha }{p}}+{\frac {1-\alpha }{r}}\right)^{-1}}$.

Their relationship is ${\displaystyle F_{\beta }=1-E}$ where ${\displaystyle \alpha ={\frac {1}{1+\beta ^{2}}}}$.

Diagnostic testing

This is related to the field of binary classification where recall is often termed "sensitivity".

		Predicted condition		Sources: [4][5][6][7][8][9][10][11] view talk edit
	Total population = P + N	Predicted positive	Predicted negative	Informedness, bookmaker informedness (BM) = TPR + TNR − 1	Prevalence threshold (PT) = ⁠√TPR × FPR - FPR/TPR - FPR⁠
Actual condition	Positive (P) [a]	True positive (TP), hit[b]	False negative (FN), miss, underestimation	True positive rate (TPR), recall, sensitivity (SEN), probability of detection, hit rate, power = ⁠TP/P⁠ = 1 − FNR	False negative rate (FNR), miss rate type II error [c] = ⁠FN/P⁠ = 1 − TPR
	Negative (N)[d]	False positive (FP), false alarm, overestimation	True negative (TN), correct rejection[e]	False positive rate (FPR), probability of false alarm, fall-out type I error [f] = ⁠FP/N⁠ = 1 − TNR	True negative rate (TNR), specificity (SPC), selectivity = ⁠TN/N⁠ = 1 − FPR
	Prevalence = ⁠P/P + N⁠	Positive predictive value (PPV), precision = ⁠TP/TP + FP⁠ = 1 − FDR	False omission rate (FOR) = ⁠FN/TN + FN⁠ = 1 − NPV	Positive likelihood ratio (LR+) = ⁠TPR/FPR⁠	Negative likelihood ratio (LR−) = ⁠FNR/TNR⁠
	Accuracy (ACC) = ⁠TP + TN/P + N⁠	False discovery rate (FDR) = ⁠FP/TP + FP⁠ = 1 − PPV	Negative predictive value (NPV) = ⁠TN/TN + FN⁠ = 1 − FOR	Markedness (MK), deltaP (Δp) = PPV + NPV − 1	Diagnostic odds ratio (DOR) = ⁠LR+/LR−⁠
	Balanced accuracy (BA) = ⁠TPR + TNR/2⁠	F1 score = ⁠2 PPV × TPR/PPV + TPR⁠ = ⁠2 TP/2 TP + FP + FN⁠	Fowlkes–Mallows index (FM) = √PPV × TPR	Matthews correlation coefficient (MCC) = √TPR × TNR × PPV × NPV - √FNR × FPR × FOR × FDR	Threat score (TS), critical success index (CSI), Jaccard index = ⁠TP/TP + FN + FP⁠

1. the number of real positive cases in the data
2. A test result that correctly indicates the presence of a condition or characteristic
3. Type II error: A test result which wrongly indicates that a particular condition or attribute is absent
4. the number of real negative cases in the data
5. A test result that correctly indicates the absence of a condition or characteristic
6. Type I error: A test result which wrongly indicates that a particular condition or attribute is present

Normalised harmonic mean plot where x is precision, y is recall and the vertical axis is F₁ score, in percentage points

Precision-Recall Curve: points from different thresholds are color coded, the point with optimal F-score is highlighted in red

Dependence of the F-score on class imbalance

Precision-recall curve, and thus the ${\displaystyle F_{\beta }}$ score, explicitly depends on the ratio ${\displaystyle r}$ of positive to negative test cases.^[12] This means that comparison of the F-score across different problems with differing class ratios is problematic. One way to address this issue (see e.g., Siblini et al., 2020^[13] ) is to use a standard class ratio ${\displaystyle r_{0}}$ when making such comparisons.

Applications

The F-score is often used in the field of information retrieval for measuring search, document classification, and query classification performance.^[14] It is particularly relevant in applications which are primarily concerned with the positive class and where the positive class is rare relative to the negative class.

Earlier works focused primarily on the F₁ score, but with the proliferation of large scale search engines, performance goals changed to place more emphasis on either precision or recall^[15] and so ${\displaystyle F_{\beta }}$ is seen in wide application.

The F-score is also used in machine learning.^[16] However, the F-measures do not take true negatives into account, hence measures such as the Matthews correlation coefficient, Informedness or Cohen's kappa may be preferred to assess the performance of a binary classifier.^[17]

The F-score has been widely used in the natural language processing literature,^[18] such as in the evaluation of named entity recognition and word segmentation.

Properties

The F₁ score is the Dice coefficient of the set of retrieved items and the set of relevant items.^[19]

• The F₁-score of a classifier which always predicts the positive class converges to 1 as the probability of the positive class increases.
• The F₁-score of a classifier which always predicts the positive class is equal to 2 * proportion_of_positive_class / ( 1 + proportion_of_positive_class ), since the recall is 1, and the precision is equal to the proportion of the positive class.^[20]
• If the scoring model is uninformative (cannot distinguish between the positive and negative class) then the optimal threshold is 0 so that the positive class is always predicted.
• F₁ score is concave in the true positive rate.^[21]

Criticism

David Hand and others criticize the widespread use of the F₁ score since it gives equal importance to precision and recall. In practice, different types of mis-classifications incur different costs. In other words, the relative importance of precision and recall is an aspect of the problem.^[22]

According to Davide Chicco and Giuseppe Jurman, the F₁ score is less truthful and informative than the Matthews correlation coefficient (MCC) in binary evaluation classification.^[23]

David M W Powers has pointed out that F₁ ignores the True Negatives and thus is misleading for unbalanced classes, while kappa and correlation measures are symmetric and assess both directions of predictability - the classifier predicting the true class and the true class predicting the classifier prediction, proposing separate multiclass measures Informedness and Markedness for the two directions, noting that their geometric mean is correlation.^[24]

Another source of critique of F₁ is its lack of symmetry. It means it may change its value when dataset labeling is changed - the "positive" samples are named "negative" and vice versa. This criticism is met by the P4 metric definition, which is sometimes indicated as a symmetrical extension of F₁.^[25]

Difference from Fowlkes–Mallows index

While the F-measure is the harmonic mean of recall and precision, the Fowlkes–Mallows index is their geometric mean.^[26]

Extension to multi-class classification

The F-score is also used for evaluating classification problems with more than two classes (Multiclass classification). A common method is to average the F-score over each class, aiming at a balanced measurement of performance.^[27]

Macro F1

Macro F1 is a macro-averaged F1 score aiming at a balanced performance measurement. To calculate macro F1, two different averaging-formulas have been used: the F1 score of (arithmetic) class-wise precision and recall means or the arithmetic mean of class-wise F1 scores, where the latter exhibits more desirable properties.^[28]

Micro F1

Micro F1 is the harmonic mean of micro precision (number of correct predictions normalized by false positives) and micro recall (number of correct predictions normalized by false negatives). Since in multi-class evaluation the overall amount of false positives equals the amount of false negatives, micro F1 is equivalent to Accuracy.^[27]

See also

• BLEU
• Confusion matrix
• Hypothesis tests for accuracy
• METEOR
• NIST (metric)
• Receiver operating characteristic
• ROUGE (metric)
• Uncertainty coefficient, aka Proficiency
• Word error rate
• LEPOR

References

1. Sasaki, Y. (2007). "The truth of the F-measure" (PDF). Teach Tutor Mater. Vol. 1, no. 5. pp. 1–5.
2. Aziz Taha, Abdel (2015). "Metrics for evaluating 3D medical image segmentation: analysis, selection, and tool". BMC Medical Imaging. 15 (29): 1–28. doi:10.1186/s12880-015-0068-x. PMC 4533825. PMID 26263899.
3. Van Rijsbergen, C. J. (1979). Information Retrieval (2nd ed.). Butterworth-Heinemann.
4. Fawcett, Tom (2006). "An Introduction to ROC Analysis" (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010. S2CID 2027090.
5. Provost, Foster; Tom Fawcett (2013-08-01). "Data Science for Business: What You Need to Know about Data Mining and Data-Analytic Thinking". O'Reilly Media, Inc.
6. Powers, David M. W. (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation". Journal of Machine Learning Technologies. 2 (1): 37–63.
7. Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
8. Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). "WWRP/WGNE Joint Working Group on Forecast Verification Research". Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
9. Chicco D, Jurman G (January 2020). "The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation". BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
10. Chicco D, Toetsch N, Jurman G (February 2021). "The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation". BioData Mining. 14 (13): 13. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
11. Tharwat A. (August 2018). "Classification assessment methods". Applied Computing and Informatics. 17: 168–192. doi:10.1016/j.aci.2018.08.003.
12. Brabec, Jan; Komárek, Tomáš; Franc, Vojtěch; Machlica, Lukáš (2020). "On model evaluation under non-constant class imbalance". International Conference on Computational Science. Springer. pp. 74–87. arXiv:2001.05571. doi:10.1007/978-3-030-50423-6_6.
13. Siblini, W.; Fréry, J.; He-Guelton, L.; Oblé, F.; Wang, Y. Q. (2020). "Master your metrics with calibration". In M. Berthold; A. Feelders; G. Krempl (eds.). Advances in Intelligent Data Analysis XVIII. Springer. pp. 457–469. arXiv:1909.02827. doi:10.1007/978-3-030-44584-3_36.
14. Beitzel., Steven M. (2006). On Understanding and Classifying Web Queries (Ph.D. thesis). IIT. CiteSeerX 10.1.1.127.634.
15. X. Li; Y.-Y. Wang; A. Acero (July 2008). Learning query intent from regularized click graphs. Proceedings of the 31st SIGIR Conference. p. 339. doi:10.1145/1390334.1390393. ISBN 9781605581644. S2CID 8482989.
16. See, e.g., the evaluation of the .
17. Powers, David M. W (2015). "What the F-measure doesn't measure". arXiv:1503.06410 [cs.IR].
18. Derczynski, L. (2016). Complementarity, F-score, and NLP Evaluation. Proceedings of the International Conference on Language Resources and Evaluation.
19. Manning, Christopher (April 1, 2009). An Introduction to Information Retrieval (PDF). Exercise 8.7: Cambridge University Press. p. 200. Retrieved 18 July 2022.{{cite book}}: CS1 maint: location (link)
20. "What is the baseline of the F1 score for a binary classifier?".
21. Lipton, Z.C., Elkan, C.P., & Narayanaswamy, B. (2014). F1-Optimal Thresholding in the Multi-Label Setting. ArXiv, abs/1402.1892.
22. Hand, David (May 2018). "A note on using the F-measure for evaluating record linkage algorithms - Dimensions". app.dimensions.ai. 28 (3): 539–547. doi:10.1007/s11222-017-9746-6. hdl:10044/1/46235. S2CID 38782128. Retrieved 2018-12-08.
23. Chicco D, Jurman G (January 2020). "The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation". BMC Genomics. 21 (6): 6. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
24. Powers, David M W (2011). "Evaluation: From Precision, Recall and F-Score to ROC, Informedness, Markedness & Correlation". Journal of Machine Learning Technologies. 2 (1): 37–63. hdl:2328/27165.
25. Sitarz, Mikolaj (2023). "Extending F1 Metric, Probabilistic Approach". Advances in Artificial Intelligence and Machine Learning. 03 (2): 1025–1038. arXiv:2210.11997. doi:10.54364/AAIML.2023.1161.
26. Tharwat A (August 2018). "Classification assessment methods". Applied Computing and Informatics. 17: 168–192. doi:10.1016/j.aci.2018.08.003.
27. Opitz, Juri (2024). "A Closer Look at Classification Evaluation Metrics and a Critical Reflection of Common Evaluation Practice". Transactions of the Association for Computational Linguistics. 12: 820–836. arXiv:2404.16958. doi:10.1162/tacl_a_00675.
28. J. Opitz; S. Burst (2019). "Macro F1 and Macro F1". arXiv:1911.03347 [stat.ML].