Epicycloid

In geometry, an epicycloid (also called hypercycloid)^[1] is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an epicycle—which rolls without slipping around a fixed circle. It is a particular kind of roulette.

The red curve is an epicycloid traced as the small circle (radius r = 1) rolls around the outside of the large circle (radius R = 3).

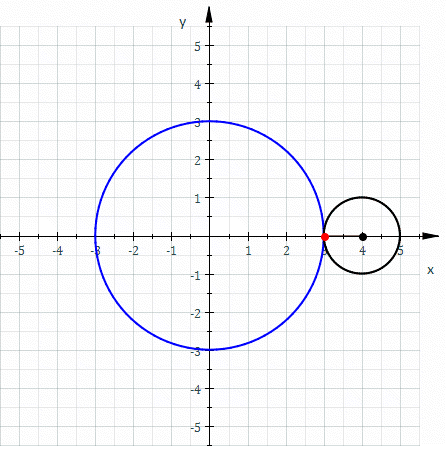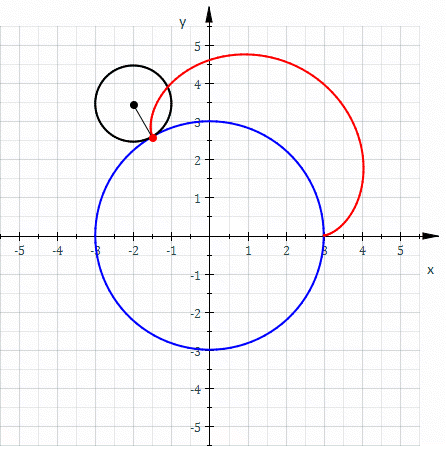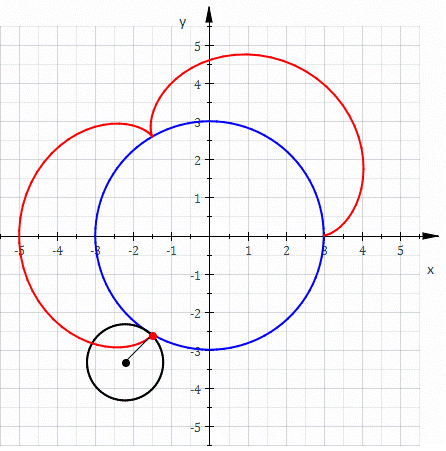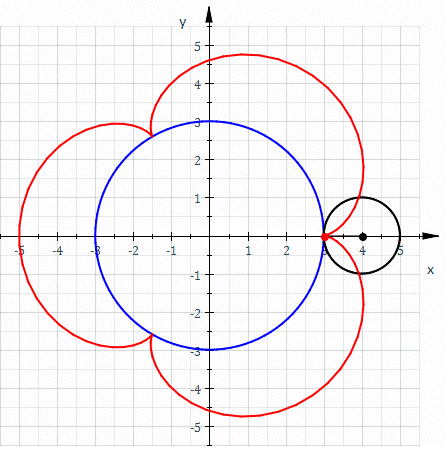
An epicycloid with a minor radius (R2) of 0 is a circle. This is a degenerate form.

Equations

If the smaller circle has radius ${\displaystyle r}$, and the larger circle has radius ${\displaystyle R=kr}$, then the parametric equations for the curve can be given by either:

${\displaystyle {\begin{aligned}&x(\theta )=(R+r)\cos \theta \ -r\cos \left({\frac {R+r}{r}}\theta \right)\\&y(\theta )=(R+r)\sin \theta \ -r\sin \left({\frac {R+r}{r}}\theta \right)\end{aligned}}}$

or:

${\displaystyle {\begin{aligned}&x(\theta )=r(k+1)\cos \theta -r\cos \left((k+1)\theta \right)\\&y(\theta )=r(k+1)\sin \theta -r\sin \left((k+1)\theta \right).\end{aligned}}}$

This can be written in a more concise form using complex numbers as^[2]

${\displaystyle z(\theta )=r\left((k+1)e^{i\theta }-e^{i(k+1)\theta }\right)}$

where

• the angle ${\displaystyle \theta \in [0,2\pi ],}$
• the smaller circle has radius ${\displaystyle r}$, and
• the larger circle has radius ${\displaystyle kr}$.

Area and Arc Length

(Assuming the initial point lies on the larger circle.) When ${\displaystyle k}$ is a positive integer, the area ${\displaystyle A}$ and arc length ${\displaystyle s}$ of this epicycloid are

${\displaystyle A=(k+1)(k+2)\pi r^{2},}$

${\displaystyle s=8(k+1)r.}$

It means that the epicycloid is ${\displaystyle {\frac {(k+1)(k+2)}{k^{2}}}}$ larger in area than the original stationary circle.

If ${\displaystyle k}$ is a positive integer, then the curve is closed, and has k cusps (i.e., sharp corners).

If ${\displaystyle k}$ is a rational number, say ${\displaystyle k=p/q}$ expressed as irreducible fraction, then the curve has ${\displaystyle p}$ cusps.

To close the curve and

complete the 1st repeating pattern :

θ = 0 to q rotations

α = 0 to p rotations

total rotations of outer rolling circle = p + q rotations

Count the animation rotations to see p and q

If ${\displaystyle k}$ is an irrational number, then the curve never closes, and forms a dense subset of the space between the larger circle and a circle of radius ${\displaystyle R+2r}$.

The distance ${\displaystyle {\overline {OP}}}$ from the origin to the point ${\displaystyle p}$ on the small circle varies up and down as

${\displaystyle R\leq {\overline {OP}}\leq R+2r}$

where

• ${\displaystyle R}$ = radius of large circle and
• ${\displaystyle 2r}$ = diameter of small circle .

• Epicycloid examples
• 
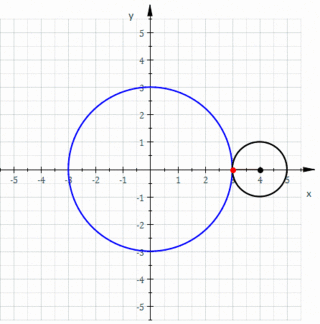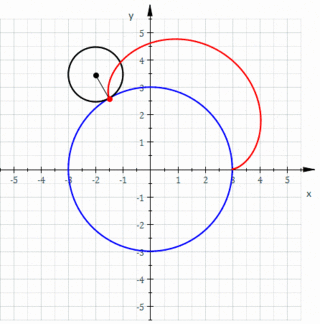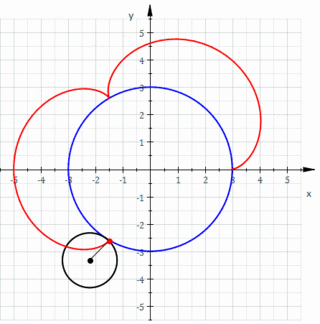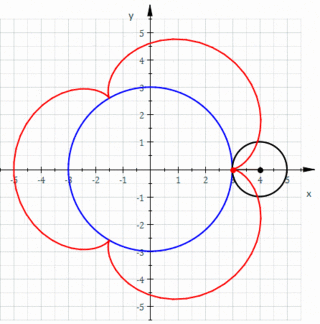
  k = 1; a cardioid
• 
  k = 2; a nephroid
• 
  k = 3; a trefoiloid
• 
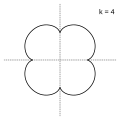
  k = 4; a quatrefoiloid
• 
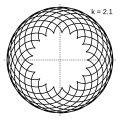
  k = 2.1 = 21/10
• 
  k = 3.8 = 19/5
• 
  k = 5.5 = 11/2
• 
  k = 7.2 = 36/5

The epicycloid is a special kind of epitrochoid.

An epicycle with one cusp is a cardioid, two cusps is a nephroid.

An epicycloid and its evolute are similar.^[3]

Proof

sketch for proof

We assume that the position of ${\displaystyle p}$ is what we want to solve, ${\displaystyle \alpha }$ is the angle from the tangential point to the moving point ${\displaystyle p}$, and ${\displaystyle \theta }$ is the angle from the starting point to the tangential point.

Since there is no sliding between the two cycles, then we have that

${\displaystyle \ell _{R}=\ell _{r}}$

By the definition of angle (which is the rate arc over radius), then we have that

${\displaystyle \ell _{R}=\theta R}$

and

${\displaystyle \ell _{r}=\alpha r}$.

From these two conditions, we get the identity

${\displaystyle \theta R=\alpha r}$.

By calculating, we get the relation between ${\displaystyle \alpha }$ and ${\displaystyle \theta }$, which is

${\displaystyle \alpha ={\frac {R}{r}}\theta }$.

From the figure, we see the position of the point ${\displaystyle p}$ on the small circle clearly.

${\displaystyle x=\left(R+r\right)\cos \theta -r\cos \left(\theta +\alpha \right)=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y=\left(R+r\right)\sin \theta -r\sin \left(\theta +\alpha \right)=\left(R+r\right)\sin \theta -r\sin \left({\frac {R+r}{r}}\theta \right)}$

See also

Animated gif with turtle in MSWLogo (Cardioid)^[4]

• List of periodic functions
• Cycloid
• Cyclogon
• Deferent and epicycle
• Epicyclic gearing
• Epitrochoid
• Hypocycloid
• Hypotrochoid
• Multibrot set
• Roulette (curve)
• Spirograph

References

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 161, 168–170, 175. ISBN 978-0-486-60288-2.

2. Epicycloids and Blaschke products by Chunlei Cao, Alastair Fletcher, Zhuan Ye
3. Epicycloid Evolute - from Wolfram MathWorld
4. Pietrocola, Giorgio (2005). "Tartapelago". Maecla.

External links

• Weisstein, Eric W. "Epicycloid". MathWorld.
• "Epicycloid" by Michael Ford, The Wolfram Demonstrations Project, 2007
• O'Connor, John J.; Robertson, Edmund F., "Epicycloid", MacTutor History of Mathematics Archive, University of St Andrews
• Animation of Epicycloids, Pericycloids and Hypocycloids
• Spirograph -- GeoFun
• Historical note on the application of the epicycloid to the form of Gear Teeth