Clausius–Clapeyron relation

"Clapeyron equation" and "Clapeyron's equation" redirect here. For a state equation, see ideal gas law.

The Clausius–Clapeyron relation, in chemical thermodynamics, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. It is named after Rudolf Clausius^[1] and Benoît Paul Émile Clapeyron.^[2] However, this relation was in fact originally derived by Sadi Carnot in his Reflections on the Motive Power of Fire, which was published in 1824 but largely ignored until it was rediscovered by Clausius, Clapeyron, and Lord Kelvin decades later.^[3] Kelvin said of Carnot's argument that "nothing in the whole range of Natural Philosophy is more remarkable than the establishment of general laws by such a process of reasoning."^[4]

Kelvin and his brother James Thomson confirmed the relation experimentally in 1849–50, and it was historically important as a very early successful application of theoretical thermodynamics.^[5] Its relevance to meteorology and climatology is the increase of the water-holding capacity of the atmosphere by about 7% for every 1 °C (1.8 °F) rise in temperature.

Definition

Exact Clapeyron equation

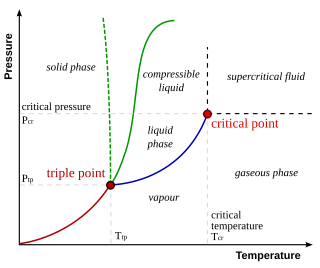
On a pressure–temperature (P–T) diagram, for any phase change the line separating the two phases is known as the coexistence curve. The Clapeyron relation^[6][7] gives the slope of the tangents to this curve. Mathematically, $${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {L}{T\,\Delta v}}={\frac {\Delta s}{\Delta v}},}$$ where ${\displaystyle \mathrm {d} P/\mathrm {d} T}$ is the slope of the tangent to the coexistence curve at any point, ${\displaystyle L}$ is the molar change in enthalpy (latent heat, the amount of energy absorbed in the transformation), ${\displaystyle T}$ is the temperature, ${\displaystyle \Delta v}$ is the molar volume change of the phase transition, and ${\displaystyle \Delta s}$ is the molar entropy change of the phase transition. Alternatively, the specific values may be used instead of the molar ones.

Clausius–Clapeyron equation

The Clausius–Clapeyron equation^[8]: 509 applies to vaporization of liquids where vapor follows ideal gas law using the ideal gas constant ${\displaystyle R}$ and liquid volume is neglected as being much smaller than vapor volume V. It is often used to calculate vapor pressure of a liquid.^[9]

$${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {PL}{T^{2}R}},}$$

$${\displaystyle v={\frac {V}{n}}={\frac {RT}{P}}.}$$

The equation expresses this in a more convenient form just in terms of the latent heat, for moderate temperatures and pressures.

Derivations

A typical phase diagram. The dotted green line gives the anomalous behavior of water. The Clausius–Clapeyron relation can be used to find the relationship between pressure and temperature along phase boundaries.

Derivation from state postulate

Using the state postulate, take the molar entropy ${\displaystyle s}$ for a homogeneous substance to be a function of molar volume ${\displaystyle v}$ and temperature ${\displaystyle T}$.^[8]: 508 $${\displaystyle \mathrm {d} s=\left({\frac {\partial s}{\partial v}}\right)_{T}\,\mathrm {d} v+\left({\frac {\partial s}{\partial T}}\right)_{v}\,\mathrm {d} T.}$$

The Clausius–Clapeyron relation describes a Phase transition in a closed system composed of two contiguous phases, condensed matter and ideal gas, of a single substance, in mutual thermodynamic equilibrium, at constant temperature and pressure. Therefore,^[8]: 508 $${\displaystyle \mathrm {d} s=\left({\frac {\partial s}{\partial v}}\right)_{T}\,\mathrm {d} v.}$$

Using the appropriate Maxwell relation gives^[8]: 508 $${\displaystyle \mathrm {d} s=\left({\frac {\partial P}{\partial T}}\right)_{v}\,\mathrm {d} v,}$$ where ${\displaystyle P}$ is the pressure. Since pressure and temperature are constant, the derivative of pressure with respect to temperature does not change.^{[10][11]: 57, 62, 671} Therefore, the partial derivative of molar entropy may be changed into a total derivative $${\displaystyle \mathrm {d} s={\frac {\mathrm {d} P}{\mathrm {d} T}}\,\mathrm {d} v,}$$ and the total derivative of pressure with respect to temperature may be factored out when integrating from an initial phase ${\displaystyle \alpha }$ to a final phase ${\displaystyle \beta }$,^[8]: 508 to obtain $${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {\Delta s}{\Delta v}},}$$ where ${\displaystyle \Delta s\equiv s_{\beta }-s_{\alpha }}$ and ${\displaystyle \Delta v\equiv v_{\beta }-v_{\alpha }}$ are respectively the change in molar entropy and molar volume. Given that a phase change is an internally reversible process, and that our system is closed, the first law of thermodynamics holds: $${\displaystyle \mathrm {d} u=\delta q+\delta w=T\,\mathrm {d} s-P\,\mathrm {d} v,}$$ where ${\displaystyle u}$ is the internal energy of the system. Given constant pressure and temperature (during a phase change) and the definition of molar enthalpy ${\displaystyle h}$, we obtain $${\displaystyle \mathrm {d} h=T\,\mathrm {d} s+v\,\mathrm {d} P,}$$ $${\displaystyle \mathrm {d} h=T\,\mathrm {d} s,}$$ $${\displaystyle \mathrm {d} s={\frac {\mathrm {d} h}{T}}.}$$

Given constant pressure and temperature (during a phase change), we obtain^[8]: 508 $${\displaystyle \Delta s={\frac {\Delta h}{T}}.}$$

Substituting the definition of molar latent heat ${\displaystyle L=\Delta h}$ gives $${\displaystyle \Delta s={\frac {L}{T}}.}$$

Substituting this result into the pressure derivative given above (${\displaystyle \mathrm {d} P/\mathrm {d} T=\Delta s/\Delta v}$), we obtain^{[8]: 508 [12]} $${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {L}{T\,\Delta v}}.}$$

This result (also known as the Clapeyron equation) equates the slope ${\displaystyle \mathrm {d} P/\mathrm {d} T}$ of the coexistence curve ${\displaystyle P(T)}$ to the function ${\displaystyle L/(T\,\Delta v)}$ of the molar latent heat ${\displaystyle L}$, the temperature ${\displaystyle T}$, and the change in molar volume ${\displaystyle \Delta v}$. Instead of the molar values, corresponding specific values may also be used.

Derivation from Gibbs–Duhem relation

Suppose two phases, ${\displaystyle \alpha }$ and ${\displaystyle \beta }$, are in contact and at equilibrium with each other. Their chemical potentials are related by $${\displaystyle \mu _{\alpha }=\mu _{\beta }.}$$

Furthermore, along the coexistence curve, $${\displaystyle \mathrm {d} \mu _{\alpha }=\mathrm {d} \mu _{\beta }.}$$

One may therefore use the Gibbs–Duhem relation $${\displaystyle \mathrm {d} \mu =M(-s\,\mathrm {d} T+v\,\mathrm {d} P)}$$ (where ${\displaystyle s}$ is the specific entropy, ${\displaystyle v}$ is the specific volume, and ${\displaystyle M}$ is the molar mass) to obtain $${\displaystyle -(s_{\beta }-s_{\alpha })\,\mathrm {d} T+(v_{\beta }-v_{\alpha })\,\mathrm {d} P=0.}$$

Rearrangement gives $${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {s_{\beta }-s_{\alpha }}{v_{\beta }-v_{\alpha }}}={\frac {\Delta s}{\Delta v}},}$$

from which the derivation of the Clapeyron equation continues as in the previous section.

Ideal gas approximation at low temperatures

When the phase transition of a substance is between a gas phase and a condensed phase (liquid or solid), and occurs at temperatures much lower than the critical temperature of that substance, the specific volume of the gas phase ${\displaystyle v_{\text{g}}}$ greatly exceeds that of the condensed phase ${\displaystyle v_{\text{c}}}$. Therefore, one may approximate $${\displaystyle \Delta v=v_{\text{g}}\left(1-{\frac {v_{\text{c}}}{v_{\text{g}}}}\right)\approx v_{\text{g}}}$$ at low temperatures. If pressure is also low, the gas may be approximated by the ideal gas law, so that $${\displaystyle v_{\text{g}}={\frac {RT}{P}},}$$

where ${\displaystyle P}$ is the pressure, ${\displaystyle R}$ is the specific gas constant, and ${\displaystyle T}$ is the temperature. Substituting into the Clapeyron equation $${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {L}{T\,\Delta v}},}$$ we can obtain the Clausius–Clapeyron equation^[8]: 509 $${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {PL}{T^{2}R}}}$$ for low temperatures and pressures,^[8]: 509 where ${\displaystyle L}$ is the specific latent heat of the substance. Instead of the specific, corresponding molar values (i.e. ${\displaystyle L}$ in kJ/mol and R = 8.31 J/(mol⋅K)) may also be used.

Let ${\displaystyle (P_{1},T_{1})}$ and ${\displaystyle (P_{2},T_{2})}$ be any two points along the coexistence curve between two phases ${\displaystyle \alpha }$ and ${\displaystyle \beta }$. In general, ${\displaystyle L}$ varies between any two such points, as a function of temperature. But if ${\displaystyle L}$ is approximated as constant, $${\displaystyle {\frac {\mathrm {d} P}{P}}\cong {\frac {L}{R}}{\frac {\mathrm {d} T}{T^{2}}},}$$ $${\displaystyle \int _{P_{1}}^{P_{2}}{\frac {\mathrm {d} P}{P}}\cong {\frac {L}{R}}\int _{T_{1}}^{T_{2}}{\frac {\mathrm {d} T}{T^{2}}},}$$ $${\displaystyle \ln P{\Big |}_{P=P_{1}}^{P_{2}}\cong -{\frac {L}{R}}\cdot \left.{\frac {1}{T}}\right|_{T=T_{1}}^{T_{2}},}$$ or^{[11]: 672 [13]} $${\displaystyle \ln {\frac {P_{2}}{P_{1}}}\cong -{\frac {L}{R}}\left({\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}\right).}$$

These last equations are useful because they relate equilibrium or saturation vapor pressure and temperature to the latent heat of the phase change without requiring specific-volume data. For instance, for water near its normal boiling point, with a molar enthalpy of vaporization of 40.7 kJ/mol and R = 8.31 J/(mol⋅K), $${\displaystyle P_{\text{vap}}(T)\cong 1~{\text{bar}}\cdot \exp \left[-{\frac {40\,700~{\text{K}}}{8.31}}\left({\frac {1}{T}}-{\frac {1}{373~{\text{K}}}}\right)\right].}$$

Clapeyron's derivation

In the original work by Clapeyron, the following argument is advanced.^[14] Clapeyron considered a Carnot process of saturated water vapor with horizontal isobars. As the pressure is a function of temperature alone, the isobars are also isotherms. If the process involves an infinitesimal amount of water, ${\displaystyle \mathrm {d} x}$, and an infinitesimal difference in temperature ${\displaystyle \mathrm {d} T}$, the heat absorbed is $${\displaystyle Q=L\,\mathrm {d} x,}$$ and the corresponding work is $${\displaystyle W={\frac {\mathrm {d} p}{\mathrm {d} T}}\,\mathrm {d} T(V''-V'),}$$ where ${\displaystyle V''-V'}$ is the difference between the volumes of ${\displaystyle \mathrm {d} x}$ in the liquid phase and vapor phases. The ratio ${\displaystyle W/Q}$ is the efficiency of the Carnot engine, ${\displaystyle \mathrm {d} T/T}$.^[a] Substituting and rearranging gives $${\displaystyle {\frac {\mathrm {d} p}{\mathrm {d} T}}={\frac {L}{T(v''-v')}},}$$ where lowercase ${\displaystyle v''-v'}$ denotes the change in specific volume during the transition.

Applications

Chemistry and chemical engineering

For transitions between a gas and a condensed phase with the approximations described above, the expression may be rewritten as ^[7] $${\displaystyle \ln \left({\frac {P_{1}}{P_{0}}}\right)={\frac {L}{R}}\left({\frac {1}{T_{0}}}-{\frac {1}{T_{1}}}\right)}$$ where ${\displaystyle P_{0},P_{1}}$ are the pressures at temperatures ${\displaystyle T_{0},T_{1}}$ respectively and ${\displaystyle R}$ is the ideal gas constant. For a liquid–gas transition, ${\displaystyle L}$ is the molar latent heat (or molar enthalpy) of vaporization; for a solid–gas transition, ${\displaystyle L}$ is the molar latent heat of sublimation. If the latent heat is known, then knowledge of one point on the coexistence curve, for instance (1 bar, 373 K) for water, determines the rest of the curve. Conversely, the relationship between ${\displaystyle \ln P}$ and ${\displaystyle 1/T}$ is linear, and so linear regression is used to estimate the latent heat.

Meteorology and climatology

Atmospheric water vapor drives many important meteorologic phenomena (notably, precipitation), motivating interest in its dynamics. The Clausius–Clapeyron equation for water vapor under typical atmospheric conditions (near standard temperature and pressure) is

$${\displaystyle {\frac {\mathrm {d} e_{s}}{\mathrm {d} T}}={\frac {L_{v}(T)e_{s}}{R_{v}T^{2}}},}$$

where

• ${\displaystyle e_{s}}$ is saturation vapor pressure,
• ${\displaystyle T}$ is temperature,
• ${\displaystyle L_{v}}$ is the specific latent heat of evaporation of water,
• ${\displaystyle R_{v}}$ is the gas constant of water vapor.

The temperature dependence of the latent heat ${\displaystyle L_{v}(T)}$ can be neglected in this application. The August–Roche–Magnus formula provides a solution under that approximation:^[15][16] $${\displaystyle e_{s}(T)=6.1094\exp \left({\frac {17.625T}{T+243.04}}\right),}$$ where ${\displaystyle e_{s}}$ is in hPa, and ${\displaystyle T}$ is in degrees Celsius (whereas everywhere else on this page, ${\displaystyle T}$ is an absolute temperature, e.g. in kelvins).

This is also sometimes called the Magnus or Magnus–Tetens approximation, though this attribution is historically inaccurate.^[17] But see also the discussion of the accuracy of different approximating formulae for saturation vapour pressure of water.

Under typical atmospheric conditions, the denominator of the exponent depends weakly on ${\displaystyle T}$ (for which the unit is degree Celsius). Therefore, the August–Roche–Magnus equation implies that saturation water vapor pressure changes approximately exponentially with temperature under typical atmospheric conditions, and hence the water-holding capacity of the atmosphere increases by about 7% for every 1 °C rise in temperature.^[18]

Example

One of the uses of this equation is to determine if a phase transition will occur in a given situation. Consider the question of how much pressure is needed to melt ice at a temperature ${\displaystyle {\Delta T}}$ below 0 °C. Note that water is unusual in that its change in volume upon melting is negative. We can assume $${\displaystyle \Delta P={\frac {L}{T\,\Delta v}}\,\Delta T,}$$ and substituting in

• ${\displaystyle L=3.34\times 10^{5}~\mathrm {J/kg} }$ (latent heat of fusion for water),
• ${\displaystyle T=273\,\mathrm {K} }$ (absolute temperature in kelvins),
• ${\displaystyle \Delta v=-9.05\times 10^{-5}~\mathrm {m^{3}/kg} }$ (change in specific volume from solid to liquid),

we obtain $${\displaystyle {\frac {\Delta P}{\Delta T}}=-13.5~{\text{MPa}}/{\text{K}}.}$$

To provide a rough example of how much pressure this is, to melt ice at −7 °C (the temperature many ice skating rinks are set at) would require balancing a small car (mass ~ 1000 kg^[19]) on a thimble (area ~ 1 cm²). This shows that ice skating cannot be simply explained by pressure-caused melting point depression, and in fact the mechanism is quite complex.^[20]

Second derivative

While the Clausius–Clapeyron relation gives the slope of the coexistence curve, it does not provide any information about its curvature or second derivative. The second derivative of the coexistence curve of phases 1 and 2 is given by^[21] $${\displaystyle {\begin{aligned}{\frac {\mathrm {d} ^{2}P}{\mathrm {d} T^{2}}}&={\frac {1}{v_{2}-v_{1}}}\left[{\frac {c_{p2}-c_{p1}}{T}}-2(v_{2}\alpha _{2}-v_{1}\alpha _{1}){\frac {\mathrm {d} P}{\mathrm {d} T}}\right]\\{}&+{\frac {1}{v_{2}-v_{1}}}\left[(v_{2}\kappa _{T2}-v_{1}\kappa _{T1})\left({\frac {\mathrm {d} P}{\mathrm {d} T}}\right)^{2}\right],\end{aligned}}}$$ where subscripts 1 and 2 denote the different phases, ${\displaystyle c_{p}}$ is the specific heat capacity at constant pressure, ${\displaystyle \alpha =(1/v)(\mathrm {d} v/\mathrm {d} T)_{P}}$ is the thermal expansion coefficient, and ${\displaystyle \kappa _{T}=-(1/v)(\mathrm {d} v/\mathrm {d} P)_{T}}$ is the isothermal compressibility.

See also

• Van 't Hoff equation
• Antoine equation
• Lee–Kesler method

References

1. Clausius, R. (1850). "Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen" [On the motive power of heat and the laws which can be deduced therefrom regarding the theory of heat]. Annalen der Physik (in German). 155 (4): 500–524. Bibcode:1850AnP...155..500C. doi:10.1002/andp.18501550403. hdl:2027/uc1.$b242250.
2. Clapeyron, M. C. (1834). "Mémoire sur la puissance motrice de la chaleur". Journal de l'École polytechnique [fr] (in French). 23: 153–190. ark:/12148/bpt6k4336791/f157.
3. Feynman, Richard (1963). "Illustrations of Thermodynamics". The Feynman Lectures on Physics. California Institute of Technology. Retrieved 13 December 2023. This relationship was deduced by Carnot, but it is called the Clausius-Clapeyron equation.
4. Thomson, William (1849). "An Account of Carnot's Theory of the Motive Power of Heat; with Numerical Results deduced from Regnault's Experiments on Steam". Transactions of the Edinburgh Royal Society. 16 (5): 541–574. doi:10.1017/S0080456800022481.
5. Pippard, Alfred B. (1981). Elements of classical thermodynamics: for advanced students of physics (Repr ed.). Cambridge: Univ. Pr. p. 116. ISBN 978-0-521-09101-5.
6. Koziol, Andrea; Perkins, Dexter. "Teaching Phase Equilibria". serc.carleton.edu. Carleton University. Retrieved 1 February 2023.
7. "Clausius-Clapeyron Equation". Chemistry LibreTexts. 2014-06-01. Retrieved 2024-10-21.
8. Wark, Kenneth (1988) [1966]. "Generalized Thermodynamic Relationships". Thermodynamics (5th ed.). New York, NY: McGraw-Hill, Inc. ISBN 978-0-07-068286-3.
9. Clausius; Clapeyron. "The Clausius-Clapeyron Equation". Bodner Research Web. Purdue University. Retrieved 1 February 2023.
10. Carl Rod Nave (2006). "PvT Surface for a Substance which Contracts Upon Freezing". HyperPhysics. Georgia State University. Retrieved 2007-10-16.
11. Çengel, Yunus A.; Boles, Michael A. (1998) [1989]. Thermodynamics – An Engineering Approach. McGraw-Hill Series in Mechanical Engineering (3rd ed.). Boston, MA.: McGraw-Hill. ISBN 978-0-07-011927-7.
12. Salzman, William R. (2001-08-21). "Clapeyron and Clausius–Clapeyron Equations". Chemical Thermodynamics. University of Arizona. Archived from the original on 2007-06-07. Retrieved 2007-10-11.
13. Masterton, William L.; Hurley, Cecile N. (2008). Chemistry : principles and reactions (6th ed.). Cengage Learning. p. 230. ISBN 9780495126713. Retrieved 3 April 2020.
14. Clapeyron, E (1834). "Mémoire sur la puissance motrice de la chaleur". Journal de l ́École Polytechnique. XIV: 153–190.
15. Alduchov, Oleg; Eskridge, Robert (1997-11-01), Improved Magnus' Form Approximation of Saturation Vapor Pressure, NOAA, doi:10.2172/548871 Equation 21 provides these coefficients.
16. Alduchov, Oleg A.; Eskridge, Robert E. (1996). "Improved Magnus Form Approximation of Saturation Vapor Pressure". Journal of Applied Meteorology. 35 (4): 601–609. Bibcode:1996JApMe..35..601A. doi:10.1175/1520-0450(1996)035<0601:IMFAOS>2.0.CO;2. Equation 25 provides these coefficients.
17. Lawrence, M. G. (2005). "The Relationship between Relative Humidity and the Dewpoint Temperature in Moist Air: A Simple Conversion and Applications" (PDF). Bulletin of the American Meteorological Society. 86 (2): 225–233. Bibcode:2005BAMS...86..225L. doi:10.1175/BAMS-86-2-225.
18. IPCC, Climate Change 2007: Working Group I: The Physical Science Basis, "FAQ 3.2 How is Precipitation Changing?". Archived 2018-11-02 at the Wayback Machine.
19. Zorina, Yana (2000). "Mass of a Car". The Physics Factbook.
20. Liefferink, Rinse W.; Hsia, Feng-Chun; Weber, Bart; Bonn, Daniel (2021-02-08). "Friction on Ice: How Temperature, Pressure, and Speed Control the Slipperiness of Ice". Physical Review X. 11 (1): 011025. doi:10.1103/PhysRevX.11.011025.
21. Krafcik, Matthew; Sánchez Velasco, Eduardo (2014). "Beyond Clausius–Clapeyron: Determining the second derivative of a first-order phase transition line". American Journal of Physics. 82 (4): 301–305. Bibcode:2014AmJPh..82..301K. doi:10.1119/1.4858403.

Bibliography

• Yau, M. K.; Rogers, R. R. (1989). Short Course in Cloud Physics (3rd ed.). Butterworth–Heinemann. ISBN 978-0-7506-3215-7.
• Iribarne, J. V.; Godson, W. L. (2013). "4. Water-Air systems § 4.8 Clausius–Clapeyron Equation". Atmospheric Thermodynamics. Springer. pp. 60–. ISBN 978-94-010-2642-0.
• Callen, H. B. (1985). Thermodynamics and an Introduction to Thermostatistics. Wiley. ISBN 978-0-471-86256-7.

Notes

1. In the original work, ${\displaystyle 1/T}$ was simply called the Carnot function and was not known in this form. Clausius determined the form 30 years later and added his name to the eponymous Clausius–Clapeyron relation.