In ten-dimensional geometry, a rectified 10-simplex is a convex uniform 10-polytope, being a rectification of the regular 10-simplex.
 10-simplex    |
 Rectified 10-simplex |
 Birectified 10-simplex | |
 Trirectified 10-simplex |
 Quadrirectified 10-simplex | ||
| Orthogonal projections in A9 Coxeter plane | |||
|---|---|---|---|
These polytopes are part of a family of 527 uniform 10-polytopes with A10 symmetry.
There are unique 5 degrees of rectifications including the zeroth, the 10-simplex itself. Vertices of the rectified 10-simplex are located at the edge-centers of the 10-simplex. Vertices of the birectified 10-simplex are located in the triangular face centers of the 10-simplex. Vertices of the trirectified 10-simplex are located in the tetrahedral cell centers of the 10-simplex. Vertices of the quadrirectified 10-simplex are located in the 5-cell centers of the 10-simplex.
Rectified 10-simplex
| Rectified 10-simplex | |
|---|---|
| Type | uniform polyxennon |
| Schläfli symbol | t1{3,3,3,3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 9-faces | 22 |
| 8-faces | 165 |
| 7-faces | 660 |
| 6-faces | 1650 |
| 5-faces | 2772 |
| 4-faces | 3234 |
| Cells | 2640 |
| Faces | 1485 |
| Edges | 495 |
| Vertices | 55 |
| Vertex figure | 9-simplex prism |
| Petrie polygon | decagon |
| Coxeter groups | A10, [3,3,3,3,3,3,3,3,3] |
| Properties | convex |
The rectified 10-simplex is the vertex figure of the 11-demicube.
Alternate names
- Rectified hendecaxennon (Acronym ru) (Jonathan Bowers)[1]
Coordinates
The Cartesian coordinates of the vertices of the rectified 10-simplex can be most simply positioned in 11-space as permutations of (0,0,0,0,0,0,0,0,0,1,1). This construction is based on facets of the rectified 11-orthoplex.
Images
| Ak Coxeter plane | A10 | A9 | A8 |
|---|---|---|---|
| Graph | |
 |
 |
| Dihedral symmetry | [11] | [10] | [9] |
| Ak Coxeter plane | A7 | A6 | A5 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Birectified 10-simplex
| Birectified 10-simplex | |
|---|---|
| Type | uniform 9-polytope |
| Schläfli symbol | t2{3,3,3,3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 8-faces | |
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 1980 |
| Vertices | 165 |
| Vertex figure | {3}x{3,3,3,3,3,3} |
| Coxeter groups | A10, [3,3,3,3,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Birectified hendecaxennon (Acronym bru) (Jonathan Bowers)[2]
Coordinates
The Cartesian coordinates of the vertices of the birectified 10-simplex can be most simply positioned in 11-space as permutations of (0,0,0,0,0,0,0,0,1,1,1). This construction is based on facets of the birectified 11-orthoplex.
Images
| Ak Coxeter plane | A10 | A9 | A8 |
|---|---|---|---|
| Graph | |
 |
 |
| Dihedral symmetry | [11] | [10] | [9] |
| Ak Coxeter plane | A7 | A6 | A5 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Trirectified 10-simplex
| Trirectified 10-simplex | |
|---|---|
| Type | uniform polyxennon |
| Schläfli symbol | t3{3,3,3,3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 8-faces | |
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 4620 |
| Vertices | 330 |
| Vertex figure | {3,3}x{3,3,3,3,3} |
| Coxeter groups | A10, [3,3,3,3,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Trirectified hendecaxennon (Jonathan Bowers)[3]
Coordinates
The Cartesian coordinates of the vertices of the trirectified 10-simplex can be most simply positioned in 11-space as permutations of (0,0,0,0,0,0,0,1,1,1,1). This construction is based on facets of the trirectified 11-orthoplex.
Images
| Ak Coxeter plane | A10 | A9 | A8 |
|---|---|---|---|
| Graph | |
 |
 |
| Dihedral symmetry | [11] | [10] | [9] |
| Ak Coxeter plane | A7 | A6 | A5 |
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Quadrirectified 10-simplex
| Quadrirectified 10-simplex | |
|---|---|
| Type | uniform polyxennon |
| Schläfli symbol | t4{3,3,3,3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 8-faces | |
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 6930 |
| Vertices | 462 |
| Vertex figure | {3,3,3}x{3,3,3,3} |
| Coxeter groups | A10, [3,3,3,3,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Quadrirectified hendecaxennon (Acronym teru) (Jonathan Bowers)[4]
Coordinates
The Cartesian coordinates of the vertices of the quadrirectified 10-simplex can be most simply positioned in 11-space as permutations of (0,0,0,0,0,0,1,1,1,1,1). This construction is based on facets of the quadrirectified 11-orthoplex.
Images
| Ak Coxeter plane | A10 | A9 | A8 |
|---|---|---|---|
| Graph | |
 |
 |
| Dihedral symmetry | [11] | [10] | [9] |
| Ak Coxeter plane | A7 | A6 | A5 |
| Graph |  |
 |
 |
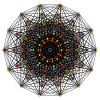| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
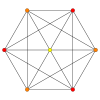| Dihedral symmetry | [5] | [4] | [3] |
Notes
References
External links
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
