Loading AI tools
From Wikipedia, the free encyclopedia
In geometry, the small stellated 120-cell or stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol {5/2,5,3}. It is one of 10 regular Schläfli-Hess polytopes.
| Small stellated 120-cell | |
|---|---|
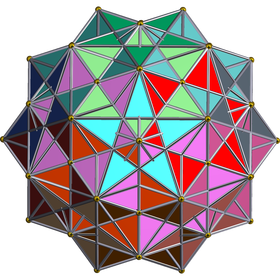Orthogonal projection | |
| Type | Schläfli-Hess polytope |
| Cells | 120 {5/2,5} |
| Faces | 720 {5/2} |
| Edges | 1200 |
| Vertices | 120 |
| Vertex figure | {5,3} |
| Schläfli symbol | {5/2,5,3} |
| Coxeter-Dynkin diagram |       |
| Symmetry group | H4, [3,3,5] |
| Dual | Icosahedral 120-cell |
| Properties | Regular |
It has the same edge arrangement as the great grand 120-cell, and also shares its 120 vertices with the 600-cell and eight other regular star 4-polytopes. It may also be seen as the first stellation of the 120-cell. In this sense it could be seen as analogous to the three-dimensional small stellated dodecahedron, which is the first stellation of the dodecahedron. Indeed, the small stellated 120-cell is dual to the icosahedral 120-cell, which could be taken as a 4D analogue of the great dodecahedron, dual of the small stellated dodecahedron.
The edges of the small stellated 120-cell are τ2 as long as those of the 120-cell core inside the 4-polytope.
| H3 | A2 / B3 / D4 | A3 / B2 |
|---|---|---|
 |
 |
 |
 | This 4-polytope article is a stub. You can help Wikipedia by expanding it. |
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
