Τετραγωνική ρίζα του 3

Η τετραγωνική ρίζα του 3 είναι ο θετικός πραγματικός αριθμός που, όταν πολλαπλασιαστεί με τον εαυτό του, δίνει τον αριθμό 3. Συμβολίζεται με ${\textstyle {\sqrt {3}}}$ ή ${\displaystyle 3^{1/2}}$. Ονομάζεται ακριβέστερα η κύρια τετραγωνική ρίζα του 3 για να διακρίνεται από τον αρνητικό αριθμό με την ίδια ιδιότητα. Η τετραγωνική ρίζα του 3 είναι ένας άρρητος αριθμός. Είναι επίσης γνωστή ως η σταθερά του Θεοδώρου, από τον Θεόδωρο τον Κυρηναίο που απέδειξε την αρρητότητά της.

Τετραγωνική ρίζα του 3

Η τετραγωνική ρίζα του 3 είναι ίση με το μήκος της κάθετης στο ορθογώνιο τρίγωνο όπου η υποτείνουσα έχει μήκος 2 και η άλλη κάθετη μήκος 1.
Αναπαραστάσεις
Δεκαδική	1.7320508075688772...
Συνεχές κλάσμα	${\displaystyle 1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+\ddots }}}}}}}}}}}$
Δυαδική	1.1011101101100111...
Δεκαεξαδική	1.BB67AE8584CAA73B...

Ως τις Ιουνίου 2024^[update], η αριθμητική της τιμή είχε υπολογιστεί σε τουλάχιστον 3 τρισεκατομμύρια ψηφία.^[1] Η δεκαδική της επέκταση, γραμμένη εδώ σε 60 δεκαδικά ψηφία, δίνεται από την ακολουθία:

1.732050807568877293527446341505872366942805253810380628055806... (ακολουθία A002194 στην OEIS)

Το κλάσμα ${\textstyle {\tfrac {97}{56}}}$ (1.732142857...) μπορεί να χρησιμοποιηθεί ως καλή προσέγγιση. Παρόλο που έχει παρονομαστή μόνο 56, διαφέρει από τη σωστή τιμή κατά λιγότερο από ${\textstyle {\frac {1}{10,000}}}$ (περίπου ${\textstyle 9.2\times 10^{-5}}$, με σχετικό σφάλμα ${\textstyle 5\times 10^{-5}}$). Η στρογγυλοποιημένη τιμή του, 1.732, έχει σχετικό σφάλμα μόλις 0,01%.

Το κλάσμα ${\textstyle {\frac {716,035}{413,403}}}$ ( 1.73205080756...) έχει σχετικό σφάλμα ${\textstyle 1\times 10^{-11}}$.

Ο Αρχιμήδης ανέφερε ένα εύρος για την τιμή της: ${\textstyle ({\frac {1351}{780}})^{2}>3>({\frac {265}{153}})^{2}}$.^[2]

Το κατώτερο όριο ${\textstyle {\frac {1351}{780}}}$ είναι μια ακριβής προσέγγιση για το ${\displaystyle {\sqrt {3}}}$ που διαφέρει από τη σωστή τιμή κατά λιγότερο από ${\textstyle {\frac {1}{608,400}}}$ (έξι δεκαδικά ψηφία, σχετικό σφάλμα ${\textstyle 3\times 10^{-7}}$) και το ανώτατο όριο ${\textstyle {\frac {265}{153}}}$ διαφέρει από τη σωστή τιμή κατά λιγότερο από ${\textstyle {\frac {2}{23,409}}}$ (τέσσερα δεκαδικά ψηφία, σχετικό σφάλμα ${\textstyle 1\times 10^{-5}}$).

Σχέσεις

Το ${\displaystyle {\sqrt {3}}}$ μπορεί να εκφραστεί ως το συνεχές κλάσμα [1; 1, 2, 1, 2, 1, 2, 1, …] (ακολουθία A040001 στην OEIS).

Επόμενως, για τον πίνακα

${\displaystyle {\begin{bmatrix}1&2\\1&3\end{bmatrix}}^{n}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}}$,

ισχύει ότι, καθώς ${\displaystyle n\to \infty }$

${\displaystyle {\sqrt {3}}=2\cdot {\frac {a_{22}}{a_{12}}}-1}$.

Επίσης μπορεί να αναπαρασταθεί με το γενικευμένο συνεχές κλάσμα όπως το

${\displaystyle [2;-4,-4,-4,...]=2-{\cfrac {1}{4-{\cfrac {1}{4-{\cfrac {1}{4-\ddots }}}}}}}$,

που είναι το [1; 1, 2, 1, 2, 1, 2, 1, …] όπου υπολογίζεται σε κάθε δεύτερο όρο.

Γεωμετρία και τριγωνομετρία

Το ύψος ενός ισόπλευρου τριγώνου με μήκος πλευράς 2 είναι ίσο με √3. Επίσης, η πλευρά αυτή είναι η υποτείνουσα ενός τριγώνου 30-60-90 με μήκος 2.

Το ύψος ενός κανονικού εξαγώνου με πλευρές μήκους 1 είναι ίσο με √3.

Η διαγώνιος του μοναδιαίου κύβου είναι √3.

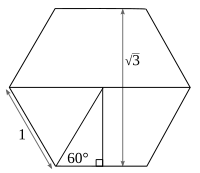
Η τετραγωνική ρίζα του 3 μπορεί να βρεθεί ως το μήκος του ύψους ενός ισόπλευρου τριγώνου με πλευρά μήκους 2.

Σε ένα ισόπλευρο τρίγωνο με πλευρές μήκους 1 κοπεί σε δύο ίσα μισά, διχοτομώντας μια εσωτερική γωνία για να σχηματιστεί μια ορθή γωνία στη μία πλευρά, η υποτείνουσα του τριγώνου της ορθής γωνίας έχει μήκος ένα και οι πλευρές του έχουν μήκος ${\textstyle {\frac {1}{2}}}$ και ${\textstyle {\frac {\sqrt {3}}{2}}}$. Από αυτό, προκύπτουν οι τριγωνομετρικοί αριθμοί

${\textstyle \tan {60^{\circ }}={\sqrt {3}}}$, ${\textstyle \sin {60^{\circ }}={\frac {\sqrt {3}}{2}}}$ και ${\textstyle \cos {30^{\circ }}={\frac {\sqrt {3}}{2}}}$.

Η τετραγωνική ρίζα του 3 εμφανίζεται επίσης σε αλγεβρικές σχέσεις για διάφορες άλλες τριγωνομετρικές σταθερές, συμπεριλαμβανομένων^[3] των ημιτόνων των 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84° και 87°.

Επίσης σε ένα κανονικό εξάγωνο με πλευρές μήκους 1, η απόσταση μεταξύ παράλληλων πλευρών είναι ${\textstyle {\sqrt {3}}}$.

Στον μοναδιαίο κύβο το μήκος της διαγωνίου είναι ίσο με ${\textstyle {\sqrt {3}}}$.

Άλλες χρήσεις και εμφανίσεις

Δυναμική μηχανική

Στην δυναμική μηχανική, η τάση μεταξύ δύο φάσεων σε ένα τριφασικό σύστημα είναι ίση με ${\textstyle {\sqrt {3}}}$ φορές τη γραμμή προς την ουδέτερη τάση. Αυτό συμβαίνει επειδή οποιεσδήποτε δύο φάσεις απέχουν 120° μεταξύ τους και δύο σημεία σε έναν κύκλο με απόσταση 120 μοιρών χωρίζονται μεταξύ τους με ${\textstyle {\sqrt {3}}}$ φορές την ακτίνα (δείτε παραδείγματα γεωμετρίας παραπάνω).

Ειδικές συναρτήσεις

Είναι γνωστό ότι οι περισσότερες ρίζες της ν-οστής παραγώγου της ${\displaystyle J_{\nu }^{(n)}(x)}$ (όπου ${\displaystyle n<18}$ και ${\displaystyle J_{\nu }(x)}$ είναι η συνάρτηση Μπέσελ πρώτου τύπου τάξης ${\displaystyle \nu }$) είναι υπερβατικές. Οι μόνες εξαιρέσεις είναι οι αριθμοί ${\displaystyle \pm {\sqrt {3}}}$, που είναι οι αλγεβρικές ρίζες της ${\displaystyle J_{1}^{(3)}(x)}$ και της ${\displaystyle J_{0}^{(4)}(x)}$.^[4]

Δείτε επίσης

• Τετραγωνική ρίζα του 2
• Τετραγωνική ρίζα του 5

Παραπομπές

Commons logo

Τα Wikimedia Commons έχουν πολυμέσα σχετικά με το θέμα    Τετραγωνική ρίζα του 3

1. Yee, Alexander. «Records Set by y-cruncher».
2. Knorr, Wilbur R. (June 1976). «Archimedes and the measurement of the circle: a new interpretation». Archive for History of Exact Sciences 15 (2): 115–140. doi:10.1007/bf00348496.

   MR 0497462

   . https://link.springer.com/article/10.1007/BF00348496. Ανακτήθηκε στις November 15, 2022.
3. Wiseman, Julian D. A. (Ιουνίου 2008). «Sin and Cos in Surds». JDAWiseman.com. Ανακτήθηκε στις 15 Νοεμβρίου 2022.
4. Lorch, Lee; Muldoon, Martin E. (1995). «Transcendentality of zeros of higher dereivatives of functions involving Bessel functions». International Journal of Mathematics and Mathematical Sciences 18 (3): 551–560. doi:10.1155/S0161171295000706.