Regressionsparameter

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (beispielsweise Einzelnachweisen) ausgestattet. Angaben ohne ausreichenden Beleg könnten demnächst entfernt werden. Bitte hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst.

Regressionsparameter, auch Regressionskoeffizienten oder Regressionsgewichte genannt, messen den Einfluss einer Variablen in einer Regressionsgleichung.^[1] Dazu lässt sich mit Hilfe der Regressionsanalyse der Beitrag einer unabhängigen Variablen (des Regressors) für die Prognose der abhängigen Variablen herleiten.

Bei einer multiplen Regression kann es sinnvoll sein, die standardisierten Regressionskoeffizienten zu betrachten, um die Erklärungs- oder Prognosebeiträge der einzelnen unabhängigen Variablen (unabhängig von den bei der Messung der Variablen gewählten Einheiten) miteinander vergleichen zu können, z. B. um zu sehen, welcher Regressor den größten Beitrag zur Prognose der abhängigen Variablen leistet.

Interpretation des Absolutglieds und der Steigung

Gegeben sei das multiple lineare Modell

${\displaystyle y_{i}=\beta _{0}+x_{i1}\beta _{1}+\dotsc +x_{ik}\beta _{k}+\varepsilon _{i}=\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }}+\varepsilon _{i}}$ bzw. in Matrixschreibweise ${\displaystyle \mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}}$.

Den Parameter ${\displaystyle \beta _{0}}$ bezeichnet man als Niveauparameter, Achsenabschnitt, Absolutglied, Regressionskonstante oder kurz Konstante (engl. intercept).

Die Parameter ${\displaystyle \beta _{1},\dotsc ,\beta _{k}}$ nennt man Steigungsparameter, Steigungskoeffizienten oder Anstieg (engl. slope).

Die ${\displaystyle \varepsilon _{i}}$ sind Störgrößen.

Man unterscheidet bei der Interpretation der Regressionskoeffizienten die folgenden Fälle:

Level-Level-Transformation

Im Fall, bei der die endogene Variable untransformiert (level) ist und die exogene Variable ebenfalls (level) gilt aufgrund von ${\displaystyle \operatorname {E} (\mathbf {y} |\mathbf {X} )=\mathbf {X} {\boldsymbol {\beta }}}$

${\displaystyle \operatorname {E} (y_{i}|\mathbf {x} _{i})=\beta _{0}+x_{i1}\beta _{1}+\dotsc +x_{ik}\beta _{k}}$.

Damit gilt für den Niveau- und den Steigungsparameter:

${\displaystyle \beta _{0}=\operatorname {E} (y_{i}|x_{i1}=x_{i2}=\dotsc =x_{ik}=0)}$

und

${\displaystyle \beta _{j}={\frac {\partial \,(y_{i}|\mathbf {x} _{i})}{\partial \,x_{ij}}}}$, ceteris paribus (c.p.), ${\displaystyle j=1,\ldots ,k}$

Der Niveauparameter lässt sich wie folgt interpretieren: Die Zielgröße ${\displaystyle y}$ beträgt im Mittel ${\displaystyle \beta _{0}}$ (bzw. ${\displaystyle {\hat {\beta }}_{0}}$) wenn alle Regressoren ${\displaystyle 0}$ sind.

Für den jeweiligen Steigungsparameter ${\displaystyle \beta _{j}}$ gilt: Steigt ${\displaystyle x_{ij}}$ c.p. um eine Einheit, dann steigt ${\displaystyle y_{i}}$ im Mittel um ${\displaystyle \beta _{j}}$-Einheiten.

Log-Log-Transformation

Im Fall, bei der die endogene Variable logarithmisch transformiert (log) ist und die exogene Variable ebenfalls (log) gilt

${\displaystyle \beta _{j}={\frac {\partial \,(\ln(y_{i}^{\dagger })|\mathbf {x} _{i})}{\partial \,\ln(x_{ij}^{\dagger })}}={\frac {\frac {\partial \,((y_{i}^{\dagger })|\mathbf {x} _{i})}{y_{i}^{\dagger }|\mathbf {x} _{i}}}{\frac {\partial \,(x_{ij}^{\dagger })}{x_{ij}^{\dagger }}}}}$, ceteris paribus (c.p.), ${\displaystyle j=1,\ldots ,k}$

Dies kann wie folgt interpretiert werden: Steigt das transformierte ${\displaystyle x_{ij}}$ c.p. um 1 %, dann steigt das transformierte ${\displaystyle y_{i}}$ im Mittel um ${\displaystyle \beta _{j}}$-Prozent. Ökonomisch würde dies der Interpretation als Elastizität entsprechen.

Standardisierte Regressionskoeffizienten

Die standardisierten Regressionskoeffizienten ${\displaystyle \beta _{j}}$ (gelegentlich auch Beta-Werte oder Beta-Gewicht genannt) ergeben sich aus einer linearen Regression, in der die unabhängigen und abhängigen Variablen standardisiert worden sind, das heißt, der Erwartungswert gleich Null und die Varianz gleich Eins gesetzt wurde. Sie können auch direkt berechnet werden aus den Regressionskoeffizienten der linearen Regression:

${\displaystyle \beta _{j}=b_{j}\cdot {\frac {s_{x_{j}}}{s_{y}}}}$

• wobei ${\displaystyle b_{j}}$ der Regressionskoeffizient für Regressor ${\displaystyle x_{j}}$,
• ${\displaystyle s_{x_{j}}}$ Standardabweichung der unabhängigen Variable ${\displaystyle x_{j}}$
• und ${\displaystyle s_{y}}$ Standardabweichung der abhängigen Variable ${\displaystyle y}$

Sind die standardisierten erklärenden Variablen ${\displaystyle Z(X_{j})}$ untereinander unabhängig und auch unabhängig vom Störterm ${\displaystyle \varepsilon }$ (Voraussetzung im klassischen Regressionsmodell), dann gilt

${\displaystyle {\begin{aligned}1={\rm {Var}}(Z(Y))&={\rm {Var}}(\beta _{0}+\beta _{1}Z(X_{1})+\ldots +\beta _{p}Z(X_{p})+\varepsilon )\\&=\beta _{1}^{2}\underbrace {{\rm {Var}}(Z(X_{1}))} _{=1}+\ldots +\beta _{p}^{2}\underbrace {{\rm {Var}}(Z(X_{p}))} _{=1}+{\rm {Var}}(\varepsilon ),\end{aligned}}}$

das heißt die Summe der quadrierten standardisierten Regressionskoeffizienten ist kleiner gleich Eins. Sind einer oder mehrere der standardisierten Regressionskoeffizienten größer als Eins bzw. kleiner als minus Eins, weist dies auf Multikollinearität hin.

Beispiel

Regressionskoeffizienten in der linearen Regression im Boston Housing Datensatz.

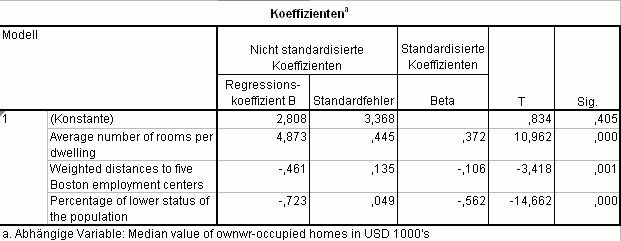
Für die abhängige Variable Mittlerer Hauspreis in selbstbewohnten Häusern pro Bezirk (in 1000 US$) aus dem Boston Housing Datensatz ergibt sich das nebenstehende Regressionsmodell:

• Jedes Zimmer zusätzlich im Haus verteuert den Kaufpreis um 4873 US$,
• jeder Kilometer mehr zu einer Arbeitsstätte reduziert den Kaufpreis um 461 US$ und
• jeder Prozentpunkt mehr beim Anteil der Unterschichtbevölkerung reduziert den Kaufpreis um 723 US$.

Standardisiert man alle Variablen, kann man den Einfluss einer erklärenden Variablen auf die abhängige Variable abschätzen:

• Den größten Einfluss hat die Variable Anteil der Unterschichtbevölkerung: −0,562,
• den zweitgrößten Einfluss hat die Variable Anzahl Zimmer: 0,372 und
• die Variable Entfernung zu Arbeitsstätten hat den geringsten Einfluss: −0,106.

Wären die Variablen unabhängig voneinander, könnte man anhand der quadrierten Regressionskoeffizienten den Anteil der erklärten Varianz angeben:

• Die Variable Anteil der Unterschichtbevölkerung erklärt knapp 32 % der Varianz des mittleren Hauspreises (${\displaystyle 0{,}316=(-0{,}562)^{2}}$),
• die Variable Anzahl Zimmer erklärt knapp 14 % der Varianz des mittleren Hauspreises (${\displaystyle 0{,}138=0{,}372^{2}}$) und
• die Variable Entfernung zu Arbeitsstätten erklärt etwas mehr als 1 % der Varianz des mittleren Hauspreises (${\displaystyle 0{,}011=(-0{,}106)^{2}}$).

Literatur

• Jürgen Bortz, Christof Schuster: Statistik für Human- und Sozialwissenschaftler. 7., vollständig überarbeitete und erweiterte Auflage. Springer, Berlin 2010, ISBN 978-3-642-12769-4.

Einzelnachweise

1. Bortz, Schuster: Statistik für Human- und Sozialwissenschaftler. Springer, Berlin / Heidelberg / New York 2010, ISBN 978-3-642-12769-4, S. 342 ff.