Hardy-Weinberg-ligevægt

Hardy-Weinberg-ligevægten (også kaldet -loven eller -fordelingen) er en model for fordelingen af genotyper givet frekvenserne af forskellige alleler. Ligevægten optræder, når man gør en række forenklende antagelser. Den benyttes ofte som samligningsgrundlag. Hvis Hardy-Weinberg-modellens forudsigelser ikke er opfyldt, må en eller flere af forudsætningerne være overtrådt.

Der er for få eller ingen kildehenvisninger i denne artikel, hvilket er et problem. Du kan hjælpe ved at angive troværdige kilder til de påstande, som fremføres i artiklen.

Hardy-Weinberg-loven illustreret ved to alleller.

Modellen

I modellen antages:

• Arten er diploid.
• Tilfældig parring, dvs., at forældrene til alle individer er tilfældigt udvalgt fra den foregående generation.
• Uendelig populationsstørrelse; i praksis kræves, at man kan se bort fra genetisk drift.
• Ingen migration, så næste generations genetiske sammensætning afspejler foregående generations genetiske sammensætning
• Ingen selektion, så den næste generation har samme genetiske sammensætning som foregående generation.
• Ikke-overlappende generationer.
• Ingen mutation.

Forskellige kilder formulerer forudsætningerne lidt forskelligt.

Hardy-Weinberg-proportioner

Hvis forudsætningerne i Hardy-Weinberg-ligevægten er opfyldt, er frekvenserne af genotyperne nemme at forudsige givet allelfrekvenserne.

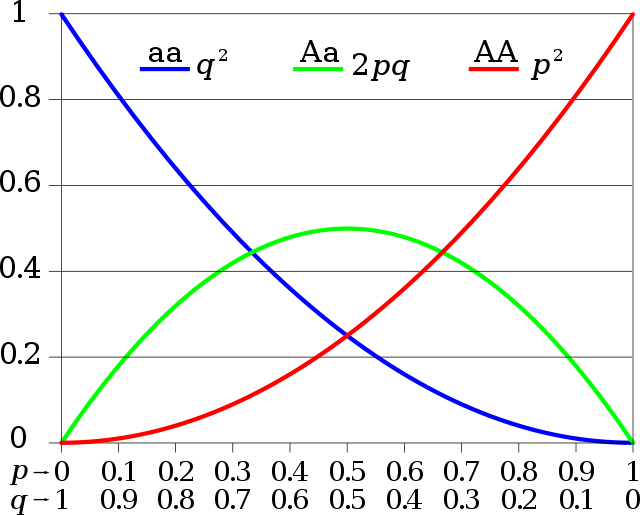
For tilfældet med to alleler A og a hhv. med frekvenserne p og q (p+q=1), forventes følgende frekvenser:^[1]

Genotype	AA	Aa	aa
Forventet frekvens	p2	2pq	q2

Denne frekvensfordeling kaldes Hardy-Weinberg proportioner. Det, at en populations genotypesammensætning er i Hardy-Weinberg proportioner, er ikke i sig selv nok til at sige, at forudsætningerne for Hardy-Weinberg Ligevægten er opfyldt. Men på den anden side gælder det, at hvis der konstateres en afvigelse fra Hardy-Weinberg proportionerne, så er en eller flere af forudsætningerne for Hardy-Weinberg Ligevægten overtrådt.

Afvigelser fra Hardy-Weinberg-proportioner

Afvigelser fra Hardy-Weinberg-proportionerne måles ved koefficienten F, som måler underskuddet af heterozygoter. Allelfrekvensen p for en allel A findes som den observerede andel af alle gener, som tilhører A-allelen. Under antagelse af Hardy-Weinberg proportionerne findes da som H_e=2p(1-p)=2pq. Den observerede andel af heterozygoter betegnes H_o. Underskuddet af heterozygoter findes da som:

${\displaystyle F={\frac {H_{e}-H_{o}}{H_{e}}}}$.

F er maksimalt 1, når der slet ikke observeres nogen heterozygoter. Under visse omstædigheder kan F blive negativ.

Test for Hardy-Weinberg-proportioner

For at undersøge, om en observeret genotypefordeling kan være fra en population i Hardy-Weinberg-proportioner, foretages normalt en χ²-test med 1 frihedsgrad. Grunden til, at der kun er 1 frihedsgrad, er, at allelfrekvensen p estimeres fra data.

Kildehenvisninger

1. Stearns, Stephen C.; Hoekstra, Rolf F. (2005). "Genetic appendix". Evolution: an introduction (engelsk) (2. udgave). Oxford University Press. s. 517-518. ISBN 978-0-19-925563-4.