Elementární (základní nebo jednotková) buňka je nejmenší část krystalické struktury. Je to rovnoběžnostěn, který je jednoznačně určen třemi translačními vektory a úhly jimi sevřenými. Mnohonásobným opakováním této buňky se beze zbytku vyplní prostor krystalu. Podle obsazení částicemi (atomy, ionty nebo molekulami) se elementární buňky rozdělují na primitivní (prosté) a složené (centrované).


V pevných látkách vytváří opakující se elementární buňka krystalové mřížky. Krystalová mřížka je pak charakterizována geometrií její elementární buňky. Elementární buňka krystalové mřížky je libovolný rovnoběžnostěn, jehož vrcholy jsou mřížkové uzly. Tato buňka je určena velikostí mřížkových vektorů umístěných do hran rovnoběžnostěnu a třemi úhly, které tyto vektory svírají. Tyto hodnoty (délka hran a, b, c, velikost úhlů α, β, γ) se označují jako parametry buňky. Jsou uspořádány podle pravotočivé vektorové soustavy, takže úhel α je mezi b a c, úhel β mezi a a c a úhel γ mezi a a b.
Dělení elementárních buněk
Podle obsazení částicemi (atomy, ionty nebo molekulami) se elementární buňky rozdělují na primitivní (prosté) a složené (centrované). Primitivní buňky jsou označované P a obsahují jeden mřížkový bod na buňku. Složené buňky obsahují více mřížkových bodů na buňku.
Všechny typy elementárních buněk a z nich vytvořených krystalových mřížek popisují prostorové Bravaisovy mřížky. Tyto mřížky reprezentují 14 jedině možných způsobů, jak je možné vyplnit prostor uzlovými body při zachování periodického uspořádání. Dělí se na 7 primitivních a 7 složených mřížek (buněk). Všechny krystalické látky mají za základ jednu z těchto mřížek. Každá krystalová struktura může mít pouze jednu Bravaisovu mřížku.[1]
Primitivní (prostá, P) buňka
Částice jsou pouze ve vrcholech rovnoběžnostěnu.
Složená (centrovaná) buňka
1.A, B, C - bazálně centrovaná, částice jsou i ve středech dvou rovnoběžných stěn a dělí se na:
- A - částice jsou umístěny ve středech přední a zadní stěny
- B - částice jsou umístěny ve středech bočních stěn
- C - částice jsou umístěny ve středech horní a dolní stěny
2. F- plošně centrovaná, částice ve středech všech stěn
3. I - prostorově centrovaná, jedna částice navíc v průsečíku tělesových úhlopříček
- Primitivní buňka (P)
- Bazálně centrovaná (C)
- Plošně centrovaná (F)
- Prostorově centrovaná (I)
Bravaisovy mřížky
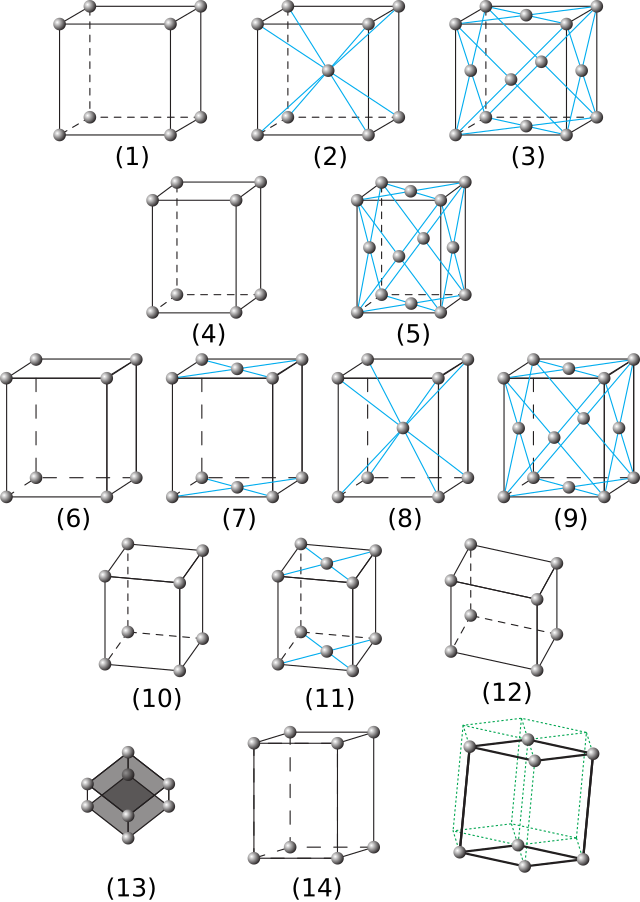
Existuje pouze 14 jedinečných možností, jak v prostoru poskládat elementární buňky a tím vznikne 14 prostorových Bravaisových mřížek. Dělí se na 7 primitivních a 7 složených mřížek (buněk). Elementární buňka musí splňovat tato Bravaisova pravidla:[2]
- Počet pravých úhlů v základní buňce musí být maximální.
- Symetrie základní buňky musí být shodná se symetrií celé mřížky.
- Při dodržení předchozích podmínek musí být objem základní buňky minimální.
- V případě, kdy symetrie nemůže rozhodnout, vybírá se základní buňka, tak aby její hrany byly co nejkratší.
Každá Bravaisova mřížka je popsána šesti základními mřížkovými parametry:
- Základní vektory (a, b, c) jsou definovány hranami základní buňky a jejich délky jsou základní periody mřížky.
- Tři úhly (α, β, γ), které svírají hrany základní buněk.
Krystalografické soustavy
Na základě vzájemného vztahu základních vektorů, můžeme vyčlenit sedm osních systémů, které odpovídají sedmi možným primitivním Bravaisovým mřížkám (buňkám). Tyto osní systémy se nazývají krystalografické soustavy. Všechny krystalické struktury, které mohou být definovány stejným systémem souřadných os, patří k téže krystalografické soustavě.
Rozlišuje se následujících sedm krystalografických soustav:
- triklinická (trojklonná), a0 ≠ b0 ≠ c0, α ≠ β ≠ γ
- monoklinická (jednoklonná), a0 ≠ b0 ≠ c0, α = γ, β > 90°
- ortorombická (kosočtverečná), a0 ≠ b0 ≠ c0, α = β = γ = 90°
- tetragonální (čtverečná), a0 = b0 ≠ c0, α = β = γ = 90°
- trigonální (klencová), a0 = b0 ≠ c0 resp. a1 = a2 = a3 ≠ c0, α = β = 90°, γ = 120°
- hexagonální (šesterečná), a0 = b0 ≠ c0 resp. a1 = a2 = a3 ≠ c0, α = β = 90°, γ = 120°
- kubická (krychlová), a = b = c, α = β = γ = 90°
Hexagonální a trigonální soustava mají sice stejný osní systém, ale zpravidla se vyčleňují zvlášť. Pro hexagonální soustavu je charakteristická přítomnost šestičetných rotačních a inverzních os symetrie, pro trigonální soustavu jsou charakteristické osy trojčetné a trojčetné inverzní.
Reference
Související články
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.




