instrument de mesura From Wikipedia, the free encyclopedia
El nònius[1] o vernier[2] és un mecanisme que permet augmentar la precisió a l'hora de mesurar distàncies o altres magnituds. Fa servir una escala secundària per indicar en aquesta escala, amb més aproximació, quan la mesura es troba entre dues marques de l'escala principal.[3][4]
En la seva forma actual va ser inventat pel matemàtic francés Pierre Vernier (1580-1637).

El nònius o vernier és una segona escala auxiliar que té algun instrument de mesura, que permet apreciar una mesura amb més precisió al complementar les divisions del regle o escala principal de l'instrument de mesura.[5]

En Pedro Nunes, conegut també pel seu nom llatí com Petrus Nonius (Alcácer do Sal, Portugal, 1492 - Coïmbra, 1577), matemàtic, astrònom i geògraf portuguès, del segle xvi, va inventar el 1514 el nònius: un dispositiu de mesura d'angles (o de longituds) que permet -quan s'incorpora a un astrolabi o aparell similar- mesurar fraccions de grau d'angle, mitjançant una escala auxiliar.
Pierre Vernier (Ornans, 1580 - Ornans, 1637) fou un matemàtic francès, és conegut per la invenció en 1631 de l'escala vernier per mesurar longituds amb gran precisió i basat en el de Pedro Nunes.[6]
Com s'ha dit la primera invenció va ser de Pedro Nunes (1514) i el posterior desenvolupament de Pierre Vernier (1631), en l'actualitat aquesta escala se sol denominar tant nònius com vernier, emprant un o altre terme segons de quin entorn es tracti. A la branca tècnica industrial sol ser més utilitzat nònius, en canvi el terme vernier és comú en l'ensenyament i en les ciències aplicades. Aquí s'ha escollit el terme nònius per ser el més antic i per tant el que va aportar la idea original, considerant, en tot cas, nònius i vernier com termes sinònims.
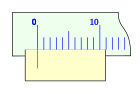
El sistema consisteix en un regle sobre el qual s'han gravat una sèrie de divisions segons el sistema d'unitats emprat, i un carro mòbil, amb un punt de mesura, que es mou al llarg del regle.
 |
 |
 |
 |
 |
En una escala de mesura podem apreciar fins a la seva unitat de divisió més petita, sent aquesta l'apreciació amb la que es pot donar la mesura; és fàcil adonar-se que entre una divisió i la següent hi ha més divisions, que unes vegades estan més a prop de la primera i altres cops de la següent.

Per poder apreciar diferents valors entre dues divisions consecutives, es va idear una segona escala que s'anomena nònius o vernier, gravada sobre la corredora i el punt zero és la línia de referència. El nònius o vernier és aquesta segona escala, no l'instrument de mesura o el tipus de mesura a realitzar, tant si és una mesura lineal, angular, o d'una altra naturalesa, i sigui quina sigui la unitat de mesura. Això és, si fem servir un regle per fer una mesura, només podem apreciar fins a la divisió més petita d'aquest regle, si a més disposem de l'esmentada segona escala, anomenada nònius o vernier, podem distingir valors més petits.
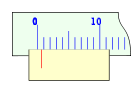
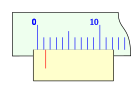
El nònius o vernier pren un fragment del regle -que en el sistema decimal és un múltiple de deu menys un: 9, 19, etc .- i el divideix en un nombre més de divisions: 10, 20, ... A la figura es prenen 9 divisions del regle i es divideixen en deu parts iguals, és el cas més senzill, de tal manera que cadascuna d'aquestes divisions sigui de 0,9 unitats del regle. Això fa que si la divisió zero del nònius coincideix amb la divisió zero del regle, la distància entre la primera divisió del regle i la primera del nònius sigui de 0,1, que entre la segona divisió del regle i la segona del nònius hi hagi una diferència de 0,2, i així, successivament, de manera que entre la desena divisió del regle i la desena del nònius hagi 1,0, és a dir: la desena divisió del nònius coincideix amb la novena del regle, segons s'ha dit en la forma de construcció del nònius. Això fa que en tots els casos en què el punt 0 del nònius coincideix amb una divisió del regle el punt deu del nònius també ho fa.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
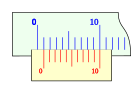
Quan la divisió un del nònius coincideix amb una divisió del regle, el fidel està separat 0,1 endavant. De manera general, el fidel indica el nombre sencer de divisions del regle, i el nònius indica la seva posició entre dues divisions successives del regle.



Una escala Nònius té quatre característiques que la defineixen:
D'aquestes variables només n i k són independents i A i L depenen de les primeres de la manera següent. L'apreciació és:
i la longitud del nònius és:
on k és un nombre enter major o igual que 1. Normalment és 1, o bé 2 quan es vol facilitar la lectura.
En el cas vist fins ara, amb n = 10, tenim que:
en el cas vist k = 1, per tant:
En el cas que k = 2, tindríem:
un nònius de 19 mm de longitud i 10 divisions tindria la mateixa apreciació en el doble de longitud, cosa que en facilita la lectura perquè les divisions estan més separades.
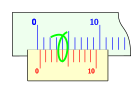
Un altre exemple de nònius amb n = 10 i k = 4 és el de la imatge. L'apreciació de l'instrument serà:
i la seva longitud és:
Aquest cas de nònius a un peu de rei no és molt usual. La seva característica més destacada és la facilitat de lectura gràcies a la gran distància entre les seves divisions. A la imatge es veu un peu de rei tancat amb aquest nònius, amb lectura 0 mm.

Podem veure un altre exemple, que juntament amb l'anterior, són els més utilitzats en el sistema decimal. Amb un nònius de 19 de longitud i 20 divisions, amb el que tindríem una apreciació:
el cas més normal és amb k = 1, per tant:
Les longituds del nònius de 10 divisions i k = 2, i de 20 divisions i k = 1 és la mateixa: 19 mm, com es pot veure, però en aquest segon cas les 20 divisions donen una apreciació de 0,05. En el cas anterior és de 0,1 per la diferència en el nombre de divisions.
Per a un peu de rei és la major apreciació, atès que divisions més petites no serien apreciables a simple vista, i seria necessari un equip òptic auxiliar.


Un nònius de 50 divisions és el de la fotografia.
L'apreciació d'aquest peu de rei com en els casos anteriors, correspon a l'expressió:
En aquesta imatge, l'apreciació del peu de rei està gravada a la part superior.
La seva longitud amb k = 1, és:
L'apreciació de l'instrument, una divisió del nònius, equival a 0,02 cada cinc divisions són
En el nònius o escala vernier, es pot veure que cada cinc divisions estan marcades amb els nombres 0, per indicar el punt de mesura i començament de l'escala, i correlativament de l'1 al 10 indicant les dècimes de mil·límetre. La segona fotografia representa en detall el nònius de la mateixa imatge, indicant la lectura: 3,58, amb dos traços vermells, un indica el 3, el valor del regle anterior al punt de mesura, i l'altra la quarta marca després del 5 al nònius.
Tot i tractar-se d'una fotografia ampliada, l'assenyalar una lectura amb més precisió de 3,6 és dificultosa. És fàcil adonar-se de les dificultats d'aquest peu de rei per diferenciar mesures d'aquesta precisió, i encara que si es fabriquen i comercialitzen peus de rei d'aquesta apreciació, en la pràctica, resultaria poc útil intentar realitzar mesures de més apreciació que 0,05 mm en un peu de rei a primera vista.
L'ús del nònius en els instruments de mesura està molt generalitzat, i es fa servir en tota mena de mesures, però és el peu de rei, sense cap dubte, on la seva utilització és més general i popular.

Aquest instrument de mesura, de gran precisió, pel seu baix cost, i per ser versàtil i pràctic, ha assolit una àmplia difusió en els més diversos àmbits.

Fins ara hem vist nònius o escala vernier, en el sistema decimal, quan una unitat inferior és la desena part, això és, un dígit a la dreta de l'anterior. En sistemes no decimals, com per exemple el sexagesimal, també es fa servir aquest sistema de mesura i l'escala del nònius es pot representar a la unitat inferior.
En el sistema sexagesimal, el de mesura d'angles per exemple, en graus, minuts i segons, on un grau són seixanta minuts i un minut seixanta segons, podem emprar un nònius de la manera següent:
Partint d'un regle graduat en graus sexagesimal podem veure que l'apreciació del nònius és:
on n és el nombre de divisions, i l'aprecia vindrà donada en graus sexagesimal, per tant podem dir:
on l'apreciació vindrà donada en minuts sexagesimal.

Buscant el nombre n de divisions entre els divisors de seixanta, tindrem una escala en minuts, per exemple per n = 6, l'apreciació serà de 10 minuts:
La longitud del Nònius en unitats del regle de mesura serà:
que per a un valor k = 1, ens donarà una longitud del nònius de:
això és:
la longitud del Nònius o vernier és de 5 graus.

Si fem k = 2, tindrem una longitud major, de manera que aconseguim unes divisions més separades, donant més claredat a la lectura i permetent gravar els valors de les divisions en alguns casos:
el que resulta:
Això és vàlid per a diferents valors de n, procurant en tot cas, que el valor de l'apreciació, resulti pràctica donant nombres rodons en la unitat que ens interessa, vegem un altre exemple.

Si prenem un valor de n = 12 i k = 1, ens donarà:
Amb el que tenim una apreciació de 5 minuts de grau, en una escala clara i perfectament coherent amb el sistema de mesura emprat.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.