Transformada de Legendre

En matemàtica es diu que dues funcions diferenciables f i g són una transformada de Legendre si cadascuna de les seves primeres derivades són funció inversa de l'altra:

${\displaystyle Df=\left(Dg\right)^{-1}}$

Interpretació geomètrica de la Transformada de Legendre.

Aleshores es diu de f i g que estan relacionades per una transformada de Legendre. Són unívoques fins a una constant additiva que normalment es fixa mitjançant el requisit addicional de

${\displaystyle f(x)+g(y)=x\,y.}$

La transformada de Legendre és la seva pròpia inversa, i està relacionada amb la integració per parts.

Aquestes funcions reben aquest nom per Adrien-Marie Legendre.

Motivació

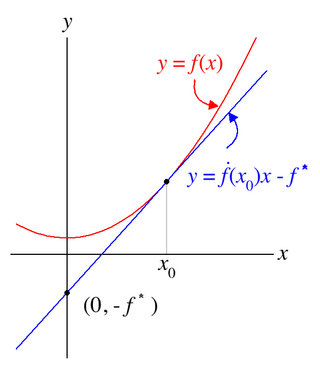
En certs problemes matemàtics o físics es desitja expressar una certa magnitud f (com l'energia interna) com funció diferent g on els arguments siguin les derivades de la funció respecte a les antigues variables. Si designem al nou argument y es té que la relació amb l'antic argument és y = df/dx.

La transformació de Legendre permet la construcció anterior, mitjançant el teorema de la funció implícita, d'una nova funció g que satisfà els requisits anteriors:

${\displaystyle g(y):=({\mathcal {L}}f)(y)=x(y)y-f(x(y))}$

on ${\displaystyle f(x)\,}$ és la funció original i ${\displaystyle {\mathcal {L}}:{\mathcal {C}}^{(2)}(D,\mathbb {R} )\to {\mathcal {C}}^{(2)}(D,\mathbb {R} )}$ és l'operador transformada de Legendre. Una funció ${\displaystyle f(x)\,}$ admet transformada de Legendre, si existeix la seva derivada segona i no s'anul·la mai.

En aquestes condicions el Teorema de la Funció Implícita aplicat a la funció:

${\displaystyle {\begin{array}{lcr}F:\mathbb {R} ^{3}&\to &\mathbb {R} \\F(x,y)&=&y-{\frac {df}{dx}}\end{array}}}$

garanteix que existeix la funció diferenciable, x(y).

Referències

• Alberty, R.A. «Use of Legendre transforms in chemical thermodynamics». Pure Appl. Chem., 73, 8, 2001. pp. 1349–1380 .
• Arnol'd, Vladimir Igorevich. Mathematical Methods of Classical Mechanics (second edition). Springer, 1989. ISBN 0-387-96890-3.
• Rockafellar, Ralph Tyrell. Convex Analysis. Princeton University Press, 1996. ISBN 0-691-01586-4.