From Wikipedia, the free encyclopedia
Una simulació d'ordinador, un model de simulació per ordinador o un model informatitzat és un programa informàtic o una xarxa d'ordinadors la finalitat del qual és crear una simulació d'un model abstracte d'un determinat sistema que està dissenyat per predir el comportament o el resultat d'un sistema físic o del món real. La fiabilitat d'alguns d'aquests models es pot determinar comparant els resultats obtinguts computacionalment amb els observats empíricament al món real. Les simulacions per ordinador s'han convertit en una part rellevant i útil dels models matemàtics de molts sistemes naturals de ciències com la física, l'astrofísica, la climatologia la química i la biologia; així com de sistemes humans d'economia, psicologia, ciències socials, ciències de la salut i enginyeria. A més es fa servir en el disseny de nova tecnologia per arribar a comprendre millor el seu funcionament.[1]
|
|
Aquest article o secció no cita les fonts o necessita més referències per a la seva verificabilitat. |
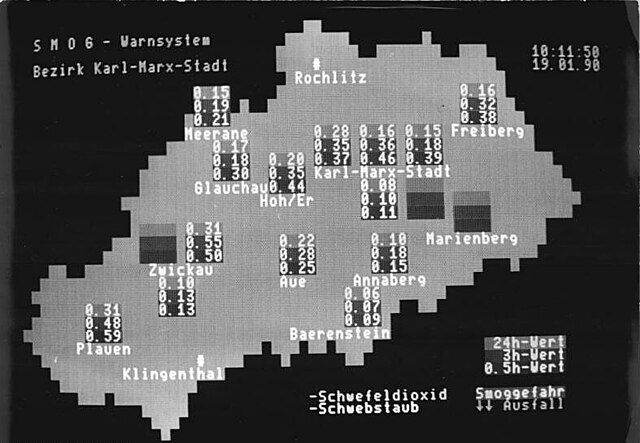
Les simulacions per ordinador abasten des de programes informàtics l'execució dels quals dura uns minuts fins a conjunts d'ordinadors connectats en xarxa l'execució dels quals dura hores o fins i tot dies. És tal el nivell de complexitat que pot arribar a assolir una simulació per ordinador, que per alguns models seria impossible (o més aviat inimaginable) reproduir els mateixos resultats fent la simulació de manera tradicional amb paper i llapis.

Un exemple de simulació de llarga durada és el projecte Blue Brain de l'Escola Politècnica federal de Lausana a Suïssa que es va iniciar el maig de 2005 per a fer la simulació per ordinador de tot el cervell humà, arribant fins i tot al nivell molecular.[2]
Cal diferenciar entre un model i una simulació. Parlem de model per a referir-nos al conjunt d'algorismes i equacions que capturen i reprodueixen el comportament del sistema que s'està simulant. Per contra, una simulació per ordinador és l'execució d'aquests algorismes i equacions. Per tant, una simulació per ordinador és com denominem al procés de fer correr un model. Segons aquest criteri, no diríem "construir una simulació", sinó "construir un model (o simulador)". Similarment, no diríem "fer correr el model", sinó que diríem "fer correr una simulació".
La simulació per ordinador es va desenvolupar alhora que es va produir el vertiginós progrés de l'ordinador. El seu primer desplegament a gran escala va ser en el Projecte Manhattan, durant la Segona Guerra Mundial, per recrear una detonació nuclear. Es tractava d'una simulació de dotze esferes emprant el mètode de Montecarlo. Les simulacions per ordinador de vegades complementen o fins i tot substitueixen els sistemes de modelització per als quals no és possible trobar solucions analítiques de forma tancada. Hi ha molts tipus de simulació per ordinador, però tots comparteixen una característica comuna: tracten de generar una mostra d'escenaris representatius per a un model en què una relació completa de tots els estats possibles seria molt costós o impossible. Els models informatitzats es van emprar inicialment com a suplement d'altres paràmetres, però més endavant el seu ús es va estendre a altres àmbits.
Els requeriments per a les dades externes de simulacions i models varia àmpliament. Per alguns models, les dades d'entrada poden ser simplement un conjunt de nombres (per exemple, la simulació d'una ona d'electricitat a un cable elèctric), mentre d'altres poden requerir terabytes sencers d'informació (com ara un model de predicció meteorològic).
Les fonts de les dades d'entrada poden variar molt. Poden donar-se en forma de:
Finalment, el moment en què podem accedir a les dades també pot mostrat variabilitat. Podem trobar:
A causa d'aquesta varietat, i també perquè diversos sistemes de simulació comparteixen molts elements, hi ha un gran ombre de llenguatges de simulació especialitzats. El més conegut podria ser Simula. Actualment n'hi ha molts més.
Els sistemes que accepten dades de fonts externes han de tenir present què és el que estan rebent exactament. Mentre que per a un ordinador és una tasca fàcil llegir dades a partir d'un fitxer de text o d'un arxiu binari, el que és molt més difícil és saber la precisió dels valors. Normalment expressem aquesta precisió amb "barres d'error", la desviació mínima i màxima dins del rang de valors per al qual esperem trobar el valor real. Com que la computació matemàtica digital no és perfecta, l'error que causen l'arrodoniment i el truncament es multiplica, per tant és útil i recomanable realitzar una «anàlisi d'error»[3] per a confirmar que els valors de les dades de sortida de la simulació seran útilment precisos.
Les simulacions per ordinador es poden classificar segons diferents parells d'atributs:
Una altra manera de categoritzar els models és mirar les estructures de dades subjacents. Per a les simulacions de temps, hi ha dues classes principals:
Les equacions defineixen les relacions existents entre els elements del sistema modelat i tracten de trobar un estat en què el sistema estigui en equilibri. Aquesta classe de models es fan servir habitualment per simular sistemes físics, és a dir, a mode de modelatge més senzill abans de passar al modelatge dinàmic.
Prèviament, a l'hora de presentar els resultats obtinguts d'una simulació per ordinador, es feien servir taules o matrius on es mostrava com les dades es veien afectades per diversos canvis als paràmetres de la simulació. L'ús d'aquest format es devia a la influencia de l'ús de matrius clàssic en l'estudi de models matemàtics. Psicòlegs i d'altres experts van adonar-se que les persones podem percebre tendències ràpidament simplement observant gràfics o fins i tot imatges en moviment generades a partir de les dades.
Fins i tot quan l'observador no és capaç d'interpretar els nombres o les fórmules, simplement mirant les gràfiques pot ser capaç d'entendre què és el que està passant a la simulació. Un bon exemple d'aquest fenomen són els mapes de simulacions meteorològiques. Gairebé qualsevol persona pot interpretar correctament una simulació del mapa de pluges dels dies vinents, i fins i tot si no som capaços de dir que és el que està passant exactament, podem arribar a la conclusió correcta ("la pluja s'apropa o s'allunya d'on sóc jo").
Similarment, les imatges generades per ordinador (Computer Generated Imagery, o CGI per les seves sigles en anglès) d'escanejos de TC poden simular com un tumor podría encongir-se o canviar durant un període estès de tractament mèdic.
Exemples genèrics de simulació per ordinador a la ciència, els quals es deriven d'una descripció matemàtica subjacent:
Exemples específics de simulacions per ordinador a la ciència:
Algunes simulacions per ordinador destacades, i polèmiques en algunes ocasions, inclouen el World3 (Món3) de Donella Meadows utilitzat en l'informe Limits to Growth (Els límits del creixement), el DaisyWorld (Món de margarides) de James Lovelock i la Tierra de Thomas Ray.
En ciències socials, la simulacio per ordinador és un component integral dels cinc angles de l'anàlisi promoguda per la metodologia de filtració de dades, que també inclou mètodes qualitatius i quantitatius, revisions en la literatura (incloent també la literatura escolar) i entrevistes amb experts. Evidentment, com a qualsevol altre mètode científic, la reproducció és una part molt important en el simulació per ordinador.
Les simulacions per ordinadors són utilitzades en molts contextos pràctics, com:
La fiabilitat i la confiança que la gent li dona a les simulacions per computador depèn en la validesa del model de simulació, per tant, la verificació i validació són crucials en el desenvolupament de simulacions per computador. Un altre aspecte important de simulacions per computador és la reproducibilitat dels resultats, és a dir, un model de simulació no hauria de donar diferents resultats a cada execució. Encara que això sembli obvi, és un punt d'atenció especial a simulacions estocàstiques, on nombres aleatoris, haurien de ser semi-aleatoris. Una excepció en la reproducibilitat són les simulacions d'homes-en-bucle, com simulacions de vol i videojocs. Aquí, l'humà és part de la simulació i per tant, influencia el resultat d'una forma que fa molt difícil, si no impossible, de reproduir exactament.
Els fabricants de vehicles utilitzen simulació per computador per testejar aparells de seguretat en nous dissenys. Mitjançant una copia d'un cotxe en una simulació física de l'entorn, poden estalviar centenars de milers d'euros, que d'altra manera, haurien estat requerits per construir i testejar un únic prototipus. Els enginyers poden realitzar una simulació en mil·lisegons per determinar els punts exactes d'estrès del prototipus en cada secció.
Els gràfics de computador poden ser utilitzats per visualitzar els resultats d'una simulació per computador. Les animacions poden ser utilitzades per experimentar una simulació a temps real, per exemple, simulacions d'entrenament. En alguns casos, les animacions poden ser també útils sent més ràpid inclús més lents que la realitat. Per exemple, animacions més ràpides que temps real poden ser útils per visualitzar la creació de cues en una simulació d'humans evacuant un edifici. A més, els resultats d'una simulació, solen estar afegits a imatges estàtiques utilitzant varies formes de visualització científica.
En la detecció d'errors, simular l'execució d'un programa sota un test (en comptes d'executar-lo sense depurar) pot permetre detectar més errors dels que la maquinària podria detectar per si mateixa i, al mateix temps, retornar informació rellevant sobre la depuració com la traça, alteracions en la memoria i el còmput d'instruccions. Aquesta tècnica també permet detectar desbordament del búffer i errors similars "difícils de detectar", a més de produir informació sobre el rendiment i ajustament de les dades.
Encara que de vegades s'ignora en les simulacions per ordinador, és molt important realitzar una anàlisi de sensibilitat per assegurar-se que la precisió dels resultats s'entén correctament. Per exemple, l'anàlisi probabilística del risc dels factors que determinen l'èxit d'un programa d'exploració de jaciments petroliers implica la combinació de mostres d'una varietat de distribucions estadístiques mitjançant el mètode de Montecarlo. Si, per exemple, un dels paràmetres clau (p.e., la proporció neta d'estrats que contenen petroli) només es coneix per una xifra significativa, aleshores el resultat de la simulació podria no ser més precís que una xifra significativa, tot i que podria (enganyosament) ser presentat amb a quatre xifres significatives.
S'han d'utilitzar els tres passos següents per produir models de simulació precisos: calibratge, verificació i validació. Les simulacions per ordinador són bones per representar i comparar escenaris teòrics, però per tal de modelar amb precisió els estudis de casos reals han de coincidir amb el que realment està passant. S'ha de crear i calibrar un model base perquè coincideixi amb l'àrea que s'està estudiant. Aleshores s'ha de verificar el model calibrat per assegurar-se que el model funciona com s'esperava en funció de les entrades. Un cop verificat el model, l'últim pas és validar el model comparant els resultats amb les dades històriques de l'àrea d'estudi. Això es pot fer utilitzant tècniques estadístiques i assegurant un valor R-quadrat adequat. A menys que s'utilitzin aquestes tècniques, el model de simulació creat produirà resultats inexactes i no serà una eina de predicció útil.
La calibració del model s'aconsegueix ajustant qualsevol paràmetre disponible per tal d'ajustar la forma en que el model opera i simula el procés. Per exemple, en una simulació de tràfic, els paràmetres més comuns inlouen la distància al front, la sensitivitat de seguiment de coches, i el temps perdut d'arrencada entre d'altres. Aquests paràmetres incluencien comportaments del conductor com ara quant de temps triga en canviar de carril, o com de ràpid comença a accelerar en creuar una intersecció. L'ajust d'aquests paràmetres tindrà un efecte directe en la quantitat de tràfic que circularà a la xarxa de carreteres del model, podent modificar-los de manera que simulin una conducció general més o menys agressiva, per exemple. Aquestes característiques són exemples de calibració que es poden afinar per tal que coincideixin amb el que es dona al món real. La gran majoria de models de simulació de tràfic tenen uns valors per defecte típics que s'ajusten prou bé a la realitat en molts dels casos, però aquests valors poden ser modificats en cas que calgui representar de forma més precisa casos o ubicacions concretes.
La verificació del model s'aconsegueix obtenint les dades de sortida del model i comprarant-les amb el que s'esperaria en funció de les dades d'entrada. Per exemple, tornant a la simulació del tràfic, podem verificar el volum de coches per assegurar-nos que el volum calculat durant tota la simulació es raonablement proper al volum de tràfic en iniciar el model. Un deu percent es considera un llindar típic a les simulacions de tràfic per a determinar si les dades de sortida s'apropen suficient a les dades d'entrada. Diferents models gestionen les dades d'entrada de diferents maneres, de manera que el tràfic que s'introdueix a la xarxa pot o no arribar a la destinació desitjada. A més a més, tràfic que podria voler introduir-se a la xarxa podria no tenir-hi accés si hi ha congestió. És per això que la verificació del model és una part molt important del procés de modelització.
L'últim pas és validar el model comparant els resultats amb el que s'esperava obtenir tenint en compte les dades històriques de l'àrea d'estudi. Idealment, el model hauria de produir uns resultats similars al que ha passat històricament. Això es verifica a través del valor R-quadrat del calibratge. Aquest valor mesura la fracció de variabilitat que s'associa al model. Un valor R-quadrat elevat no implica necessàriament que el model estigui ben entrenat. Una altra eina utilitzada per validar models és l'anàlisi de les gràfiques de residus. Si els resultats del model són completament diferents del de les dades històriques, probablement hi hagi un error en el model. Abans d'utilitzar aquest model com una base per produir nous models, és important validar-lo amb diferents escenaris i comprovar que el model funciona correctament per a cadascun d'ells. Si els resultats no concorden amb les dades històriques durant el procés de validació, s'ha de revisar el model i actualitzar-lo perquè produeixi uns resultats més similars al que s'espera. És un procés iteratiu que permet produir models més realistes.
Validar models de simulació de tràfic requereix comparar el tràfic calculat per un model amb el tràfic observat a les carreteres i als sistemes de trànsit. Les comparacions inicials es fan amb itineraris entre quadrants, sectors o altres grans zones d'interès. El pas següent és comparar el tràfic estimat pels models amb el tràfic real, incloent el nombre de viatges, que creua barreres artificials creades en l'àrea d'estudi. Aquestes barreres es solen anomenar línies de control i poden ser barreres imaginàries o físiques. Aquestes línies de control delimiten unes zones concretes de l'àrea d'estudi com poden ser el districte empresarial principal de la ciutat o altres zones que representin el centre d'activitats importants. El nombre de viatges s'acostumen a validar comparant-los amb el nombre real de vehicles que creuen les línies de control que envolten el districte empresarial principal.
Tres fonts d'error que poden causar baixa correlació durant la calibració: error d'entrada, error del model, i error de paràmetres. En general, l'error d'entrada i el de paràmetres, poden ser ajustats fàcilment per l'usuari. L'error del model, en canvi, és causat per la metodologia emprada en el model i pot no ser tan fàcil d'arreglar. Els models de simulació, normalment són construïts mitjançant diferents teories de modelatge que poden produir conflictes en els errors. Alguns models són més generals, mentre altres són més detallats. Si hi ha algun error en el model com a resultat, podria ser necessari ajustar la metodologia del model per fer els resultats més consistents.
Per tal de produir bons models que puguin retornar resultats realistes, aquests són els passos necessaris que s'han de seguir per tal de garantir que els models de simulació estan funcionant correctament. Els models de simulació poden ser utilitzats com a eina per verificar teories d'enginyeria, però són vàlids només si són ben calibrats. Una vegada s'han obtingut estimacions satisfactories dels paràmetres per tots els models, aquests han de ser comprobats per assegurar que es comporten de forma adecuada a l'executar les funcions esperades. El procés de validació estableix la credibilitat del model demostrant l'habilitat de replicar la realitta. La importància de la validació del model subralla la necessitat de planejar de forma curosa, minuciosa i precisa del programa de col·lecció de dades d'entrada que tenen aquest propòsit. Per exemple, en anàlisi de tràfic, és típic per un enginyer de tràfic fer una visita per verificar la quantitat de tràfic i familiaritzar-se amb els patrons de tràfic de l'àrea. Els models resultants i prediccions no seran millors que les dades emprades per l'estimació i validació del model.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.