qualsevol dels deu símbols (0, 1, 2, 3, 4, 5, 6, 7, 8, i 9) From Wikipedia, the free encyclopedia
Els nombres (o numerals) aràbics, també anomenats nombres indoaràbics, són els símbols més utilitzats per representar nombres. Se'ls diu «aràbics» perquè els andalusins els introduïren a Europa per la seua acció cultural, tot i que, en realitat, sorgiren a l'Índia. El món li deu a la cultura índia l'invent transcendental del sistema de numeració posicional, així com el descobriment del zero, anomenat śūnya (shuunia) o bindu en sànscrit, tot i que els maies també coneixien tant el zero com la numeració posicional. Els matemàtics perses de l'Índia n'adoptaren el sistema, dels quals el prengueren els àrabs. Quan es comencen a usar al nord d'Àfrica, ja tenien la forma actual, d'allí foren adoptats a Europa en l'edat mitjana. El seu ús augmentà arreu del món per la colonització europea.[1]
_2013-04-9_15-59.jpg)
El sistema «aràbic» es representa utilitzant conjunts de glifs diferents, que es poden dividir en dues grans famílies: els numerals aràbics occidentals i els orientals. Els orientals, que es desenvoluparen en el qual ara és l'Iraq, es representen en la taula que ve tot seguit com a «arabigoíndics». Els arabigoíndics orientals són una varietat dels glifs arabigoíndics. Els numerals aràbics occidentals, desenvolupats a l'Àndalus i al Magrib, es mostren en la taula com a «nombres aràbics moderns»:
| Nombres aràbics moderns | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Arabigoíndic | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ |
| Arabigoíndic oriental
(persa i urdu) |
۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ |
| Devanagari
(hindi) |
० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ |
| Tamil | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ |
Al Japó, els nombres «aràbics» i l'alfabet llatí formen part del sistema d'escriptura rōmaji. Així, si un nombre està escrit amb glifs «aràbics», al Japó diran que «està escrit en rōmaji» en contraposició a la numeració japonesa.
El sistema de numeració aràbic es considera un dels avanços més significatius de les matemàtiques. La majoria d'historiadors coincideixen que s'originà a l'Índia (els àrabs es refereixen a aquest sistema de numeració com a «nombres indis»), s'expandí pel món islàmic i d'ací, per l'Àndalus, a la resta d'Europa.
Sembla que l'origen del sistema posicional de base 10 emprat a l'Índia tingué l'origen a la Xina. El sistema xinés Hua Ma (vegeu numeració xinesa) és també posicional i de base 10 i pogué haver inspirat el sistema indi. Aquesta hipòtesi cobra força pel fet que entre els s. V i viii (període durant el qual s'expandeix el sistema numèric indi) hi hagué una gran afluència de pelegrins budistes entre Xina i l'Índia. En l'època de Bhaskara I (s. VII) a l'Índia s'usava un sistema numeral posicional de base 10 amb 9 glifs, i es coneixia el concepte del zero, representat per un punt.
Aquest sistema de numeració arriba a l'Orient Mitjà cap a l'any 670. Alguns matemàtics musulmans de l'actual l'Iraq, com al-Khwarazmí, estaven familiaritzats amb la numeració babilònica, que usava el zero entre dígits diferents de zero (tot i que no després de dígits diferents de zero), així que el nou sistema no tingué bona rebuda. Al segle x els matemàtics àrabs inclogueren en el seu sistema de numeració les fraccions. Al-Khwarazmí escrigué Sobre els càlculs amb els nombres de l'Índia cap a l'any 825 i Al-Kindí escrigué L'ús dels nombres de l'Índia en quatre volums. El seu treball fou molt important en la difusió del sistema de l'Índia en l'Orient Mitjà i en l'Occident.[2]
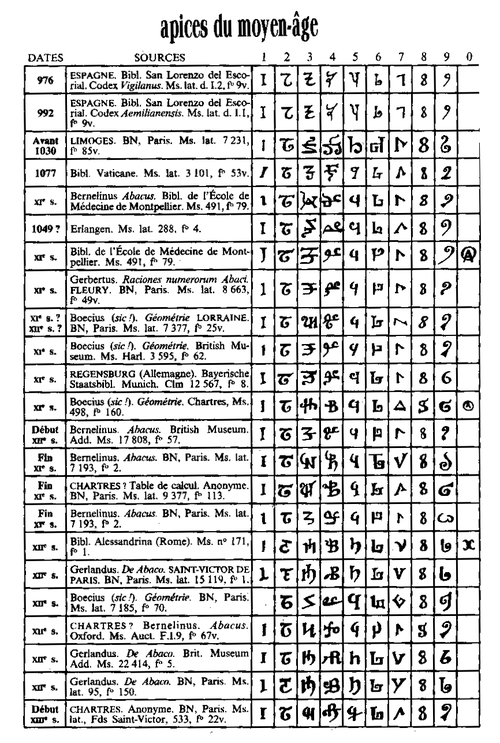
Els primers esments d'aquests numerals a Occident apareixen en el Codex Vigilanus de l'any 976.[3] A partir de 980 Gerbert d'Orlhac (més tard papa amb el nom de Silvestre II) difongué el coneixement del sistema a Europa. Leonardo de Pisa, un matemàtic italià que havia estudiat a Bugia (a actual Algèria), contribuí a la difusió per Europa del sistema aràbic amb el seu llibre Liber Abaci, publicat al 1202. Entre els primers països hi havia Gran Bretanya, en tenien escrits del 1448 a Berkshire (Anglaterra) i a Escòcia al 1470, a la tomba d'Eral de Huntly.[4] En l'Europa central, el rei d'Hongria Ladislau el Pòstum començà a usar els nombres aràbics a partir del 1456.[5]
Amb la invenció de la impremta per part de Gutenberg al 1450 aquest sistema de numeració s'usa de manera generalitzada a Europa; al s. XV s'utilitzava àmpliament; d'altra banda, els nombres aràbics reemplaçaren la numeració ciríl·lica a Rússia al voltant de 1700, quan els introduí el tsar Pere I de Rússia.
 |
|
Curiosament, en el món musulmà només els matemàtics usaven el sistema de numeració aràbic fins a temps relativament recents. Els científics hi usaven el sistema babilònic i els comerciants el grec i hebreu.
D'entre les diverses explicacions folklòriques i pseudocientífiques sobre l'origen dels numerals aràbics moderns, n'hi ha diverses d'ençà del segle xi que proposen que les formes originals dels símbols indicaven el seu valor amb la quantitat d'angles que contenien, o que cada nombre és la suma d'una distribució visual de punts o de ratlles sobre un pla.[6]
Aquestes hipòtesis són propagades amb arguments aparentment ben construïts, però estan basades en especulacions d'individus sense coneixement dels fets arqueològics, historiogràfics o cal·ligràfics rellevants ni evidències científiques.[6][7]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
