Efecte geodèsic

L'efecte geodèsic (també conegut com a precessió geodèsica, precessió de Sitter o efecte de Sitter) representa l'efecte de la curvatura de l'espai-temps, predit per la relativitat general, sobre un vector transportat amb un cos en òrbita. Per exemple, el vector podria ser el moment angular d'un giroscopi que orbita la Terra, tal com va dur a terme l'experiment Gravity Probe B. L'efecte geodèsic va ser predit per primera vegada per Willem de Sitter el 1916, que va proporcionar correccions relativistes al moviment del sistema Terra-Lluna. L'obra de De Sitter va ser ampliada el 1918 per Jan Schouten i el 1920 per Adriaan Fokker.^[1] També es pot aplicar a una precessió secular particular d'òrbites astronòmiques, equivalent a la rotació del vector Laplace–Runge–Lenz.^[2]

Una representació de l'efecte geodèsic, amb valors de Gravity Probe B.

El terme efecte geodèsic té dos significats lleugerament diferents, ja que el cos en moviment pot estar girant o no girant. Els cossos que no giren es mouen en geodèsics, mentre que els cossos que giren es mouen en òrbites lleugerament diferents.

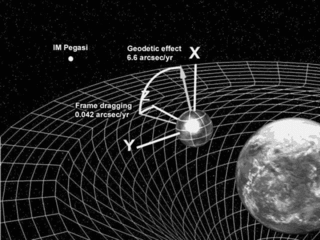
La diferència entre la precessió de De Sitter i la precessió Lense-Thirring (arrossegament del marc) és que l'efecte de Sitter es deu simplement a la presència d'una massa central, mentre que la precessió Lense-Thirring es deu a la rotació de la massa central. La precessió total es calcula combinant la precessió de De Sitter amb la precessió Lense-Thirring.^[3]

Confirmació experimental

L'efecte geodèsic es va verificar amb una precisió superior al 0,5% per cent per Gravity Probe B, un experiment que mesura la inclinació de l'eix de gir dels giroscopis en òrbita al voltant de la Terra.^[4] Els primers resultats es van anunciar el 14 d'abril de 2007 a la reunió de l'American Physical Society.

Fórmules

Per derivar la precessió, suposem que el sistema està en una mètrica de Schwarzschild rotativa. La mètrica no rotativa és

${\displaystyle ds^{2}=dt^{2}\left(1-{\frac {2m}{r}}\right)-dr^{2}\left(1-{\frac {2m}{r}}\right)^{-1}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi '^{2}),}$

on c = G = 1.

Introduïm un sistema de coordenades giratori, amb una velocitat angular ${\displaystyle \omega }$, de manera que un satèl·lit en òrbita circular a la θ = El pla π/2 roman en repòs. Això ens dóna

En aquest sistema de coordenades, un observador a la posició radial r veu que un vector situat a r gira amb freqüència angular ω. Aquest observador, però, veu un vector posicionat en algun altre valor de r com a rotació a una velocitat diferent, a causa de la dilatació relativista del temps. Transformant la mètrica de Schwarzschild en el marc giratori, i assumint això ${\displaystyle \theta }$ és una constant, trobem

${\displaystyle {\begin{aligned}ds^{2}&=\left(1-{\frac {2m}{r}}-r^{2}\beta \omega ^{2}\right)\left(dt-{\frac {r^{2}\beta \omega }{1-2m/r-r^{2}\beta \omega ^{2}}}\,d\phi \right)^{2}-\\&-dr^{2}\left(1-{\frac {2m}{r}}\right)^{-1}-{\frac {r^{2}\beta -2mr\beta }{1-2m/r-r^{2}\beta \omega ^{2}}}\,d\phi ^{2},\end{aligned}}}$

amb ${\displaystyle \beta =\sin ^{2}(\theta )}$. Per a un cos que orbita en el θ = pla π/2, tindrem β = 1, i la línia mundial del cos mantindrà les coordenades espacials constants durant tot el temps. Ara, la mètrica està en la forma canònica

${\displaystyle ds^{2}=e^{2\Phi }\left(dt-w_{i}\,dx^{i}\right)^{2}-k_{ij}\,dx^{i}\,dx^{j}.}$

A partir d'aquesta forma canònica, podem determinar fàcilment la velocitat de rotació d'un giroscopi en el moment adequat

${\displaystyle {\begin{aligned}\Omega &={\frac {\sqrt {2}}{4}}e^{\Phi }[k^{ik}k^{jl}(\omega _{i,j}-\omega _{j,i})(\omega _{k,l}-\omega _{l,k})]^{1/2}=\\&={\frac {{\sqrt {\beta }}\omega (r-3m)}{r-2m-\beta \omega ^{2}r^{3}}}={\sqrt {\beta }}\omega .\end{aligned}}}$

on l'última igualtat és certa només per als observadors de caiguda lliure per als quals no hi ha acceleració, i per tant ${\displaystyle \Phi ,_{i}=0}$. Això porta a

${\displaystyle \Phi ,_{i}={\frac {2m/r^{2}-2r\beta \omega ^{2}}{2(1-2m/r-r^{2}\beta \omega ^{2})}}=0.}$

La resolució d'aquesta equació per a ω s'obté

${\displaystyle \omega ^{2}={\frac {m}{r^{3}\beta }}.}$

Aquesta és essencialment la llei de períodes de Kepler, que resulta ser relativistament exacta quan s'expressa en termes de la coordenada temporal t d'aquest sistema de coordenades giratori particular. En el marc giratori, el satèl·lit roman en repòs, però un observador a bord del satèl·lit veu el vector de moment angular del giroscopi precesant a la velocitat ω. Aquest observador també veu que les estrelles llunyanes giren, però giren a una velocitat lleugerament diferent a causa de la dilatació del temps. Sigui τ el temps propi del giroscopi. Aleshores

${\displaystyle \Delta \tau =\left(1-{\frac {2m}{r}}-r^{2}\beta \omega ^{2}\right)^{1/2}\,dt=\left(1-{\frac {3m}{r}}\right)^{1/2}\,dt.}$

El terme −2 m / r s'interpreta com la dilatació del temps gravitatòria, mentre que el −m / r addicional es deu a la rotació d'aquest marc de referència. Sigui α' la precessió acumulada en el marc giratori. Des que ${\displaystyle \alpha '=\Omega \Delta \tau }$, la precessió al llarg d'una òrbita, en relació amb les estrelles llunyanes, ve donada per:

${\displaystyle \alpha =\alpha '+2\pi =-2\pi {\sqrt {\beta }}{\Bigg (}\left(1-{\frac {3m}{r}}\right)^{1/2}-1{\Bigg )}.}$

Amb una sèrie de Taylor de primer ordre trobem

${\displaystyle \alpha \approx {\frac {3\pi m}{r}}{\sqrt {\beta }}={\frac {3\pi m}{r}}\sin(\theta ).}$

Referències

1. Jean Eisenstaedt. Studies in the History of General Relativity (en anglès). Birkhäuser, 1988, p. 42. ISBN 0-8176-3479-7.
2. de Sitter, W Mon. Not. R. Astron. Soc., 77, 1916, pàg. 155–184. Bibcode: 1916MNRAS..77..155D. DOI: 10.1093/mnras/77.2.155 [Consulta: free].
3. jonah. «The Geodetic Effect: Measuring the Curvature of Spacetime» (en anglès americà), 28-12-2015. [Consulta: 22 setembre 2024].
4. Everitt, C.W.F.. «Gravity Probe B Science Results—NASA Final Report» (en anglès). [Consulta: 2 maig 2009].