Conjunt de les parts

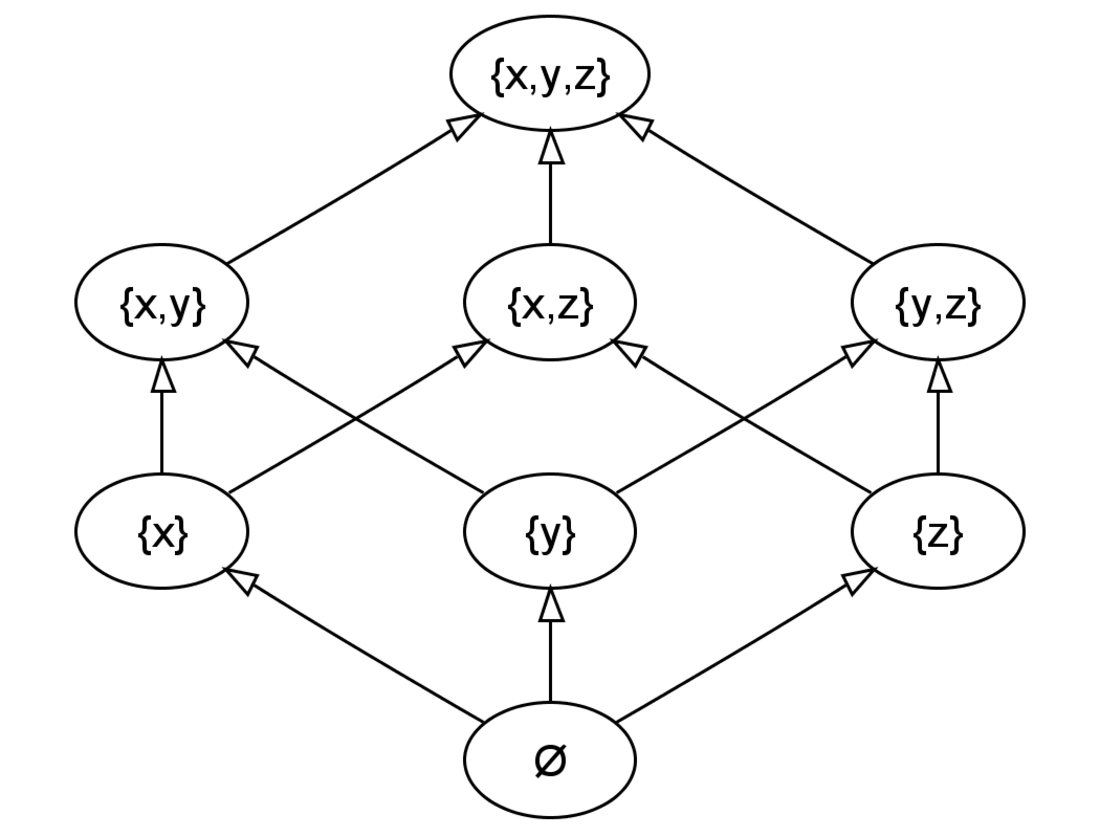
Donat un conjunt S, es defineix el conjunt de les parts de S o conjunt potència de S, escrit ${\displaystyle {\mathcal {P}}(S)}$, P(S), ℘(S), o 2^S, com el conjunt de tots els subconjunts de S. Per exemple, si S és el conjunt {a, b, c} aleshores la llista completa dels subconjunts de S és:

• {Ø} (conjunt buit)
• {a}
• {b}
• {c}
• {a,b}
• {a,c}
• {b,c}
• {a,b,c}

Diagrama del conjunt de les parts.

Per tant, el conjunt de les parts de S serà:

${\displaystyle {\mathcal {P}}(S)=\{\varnothing ,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}}$

Si S és un conjunt finit amb card (S) = n elements, aleshores el conjunt de les parts de S conté card(℘(S))= 2ⁿ elements.

La notació 2S

En la teoria de conjunts, X^Y és el conjunt de totes les funcions d'Y a X. Com que 2 pot ser definit com a {0, 1} (vegeu nombre natural), 2^S és el conjunt de totes les funcions de S a {0, 1}. Cada funció en 2^S està en correspondència bijectiva amb un subconjunt de S (l'antiimatge d'1) i, per tant, els dos conjunts 2^S i ${\displaystyle {\mathcal {P}}(S)}$ són equipotents.