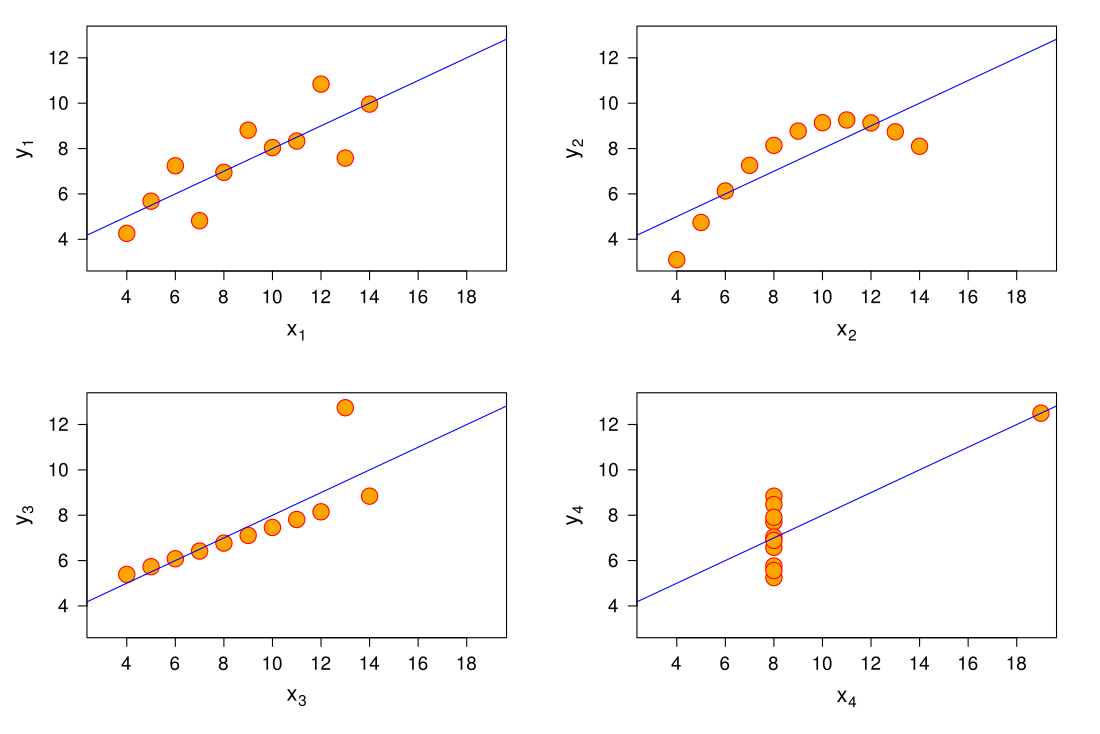
El quartet d'Anscombe comprèn quatre conjunts de dades que tenen les mateixes propietats estadístiques (mitjana, variància, etc.), però que són evidentment diferents quan s'inspeccionen visualment les seves gràfiques.

Cada conjunt està compost per 11 punts en el pla (x,y) i van ser creats per l'estadístic F. J. Anscombe. El quartet és una demostració de la importància de realitzar una inspecció visual de les dades abans d'analitzar-les.[1]
Pels quatre conjunts de dades es compleix:
El primer gràfic (a dalt a l'esquerra) mostra el que sembla una relació lineal típica, corresponent a dues variables correlacionades, cumplint amb la suposició de normalitat. El segon gràfic (a dalt a la dreta) no està distribuït normalment, tot i que s'observa una relació entre les dades, no lineal, sent en aquest cas el coeficient de correlació de Pearson irrellevant. A la tercera gràfica (a baix a l'esquerra) la distribució és lineal excepte per la presencia d'un punt que fa canviar la recta de regressió i disminuir el coeficient de correlació del valor 1 a 0.816. Finalment, la quarta gràfica (a baix a la dreta) és un altre exemple de com un valor atípic és suficient per a obtenir una correlació elevada entre dues variables fins i tot quan la relació no és lineal.
| I | II | III | IV | ||||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
Edward Tufte va usar el quartet en la primera pàgina del primer capítol del seu llibre The Visual Display of Quantitative Information, per a emfatitzar la importància de mirar les dades abans d'analitzar-les.[2]
Referències
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
 ...
...