Mitjana harmònica

La mitjana harmònica d'una quantitat finita de n nombres ${\displaystyle a_{1},a_{2},...,a_{n}}$, és igual a:^[1][2][3]

${\displaystyle {H}={n \over {\sum _{i=1}^{n}{1 \over a_{i}}}}={n \over ({1 \over a_{1}}+\cdots +{1 \over a_{n}})}}$

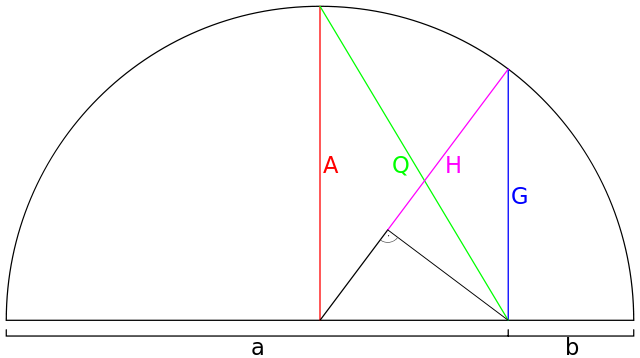Construcció geomètrica per a trobar les mitjanes aritmètica (A), quadràtica (Q), geomètrica (G) i harmònica (H) de dos nombres a i b.

Per exemple, la mitjana harmònica de 2, 6 i 12 és:

${\displaystyle {H}={3 \over ({1 \over 2}+{1 \over 6}+{1 \over 12})}=4}$

Avantatges

• Per al seu càlcul s'utilitzen totes les dades.
• És recursiva.
• Si canviem l'escala de les unitats en què es mesura la variable, la mesura canvia d'igual manera.
• És única.
• Els valors extrems (molt grans) influeixen poc.
• És senzilla de calcular.

Inconvenients

• No sempre existeix. De fet, la mitjana harmònica no està definida per a valors nuls.
• Els valors propers a zero influeixen molt en el seu valor.
• En ser sensible al canvi d'escala en les unitats, no es pot utilitzar per comparar variables que es mesurin en unitats diferents.
• El seu significat és poc intuïtiu.
• No sol incloure's en calculadores i programes per a ordinador.

Referències

1. «Calculadora mitjana harmònica». [Consulta: 25 gener 2022].
2. «HarmonicMean—Wolfram Language Documentation». [Consulta: 25 gener 2022].
3. «Averages, Arithmetic and Harmonic Means». [Consulta: 25 gener 2022].