A continuació donem una llista de tensors d'inèrcia mesurats respecte als eixos principals d'inèrcia . Juntament amb el teorema de Steiner i canvis de base, podem obtenir, en tots els casos, el tensor d'inèrcia en un altre punt del sòlid i amb una altra orientació.
Més informació
Descripció Figura Tensor d'inèrcia
Esfera sòlida de radi r i massa m .
I
=
[
2
5
m
r
2
0
0
0
2
5
m
r
2
0
0
0
2
5
m
r
2
]
{\displaystyle I={\begin{bmatrix}{\frac {2}{5}}mr^{2}&0&0\\0&{\frac {2}{5}}mr^{2}&0\\0&0&{\frac {2}{5}}mr^{2}\end{bmatrix}}}
Esfera buida de radi r i massa m .
I
=
[
2
3
m
r
2
0
0
0
2
3
m
r
2
0
0
0
2
3
m
r
2
]
{\displaystyle I={\begin{bmatrix}{\frac {2}{3}}mr^{2}&0&0\\0&{\frac {2}{3}}mr^{2}&0\\0&0&{\frac {2}{3}}mr^{2}\end{bmatrix}}}
El·lipsoide sòlid de semieixos a , b , c i massa m .
I
=
[
1
5
m
(
b
2
+
c
2
)
0
0
0
1
5
m
(
a
2
+
c
2
)
0
0
0
1
5
m
(
a
2
+
b
2
)
]
{\displaystyle I={\begin{bmatrix}{\frac {1}{5}}m(b^{2}+c^{2})&0&0\\0&{\frac {1}{5}}m(a^{2}+c^{2})&0\\0&0&{\frac {1}{5}}m(a^{2}+b^{2})\end{bmatrix}}}
Con circular recte de radi r , altura h i massa m , respecte al seu vèrtex.
I
=
[
3
5
m
h
2
+
3
20
m
r
2
0
0
0
3
5
m
h
2
+
3
20
m
r
2
0
0
0
3
10
m
r
2
]
{\displaystyle I={\begin{bmatrix}{\frac {3}{5}}mh^{2}+{\frac {3}{20}}mr^{2}&0&0\\0&{\frac {3}{5}}mh^{2}+{\frac {3}{20}}mr^{2}&0\\0&0&{\frac {3}{10}}mr^{2}\end{bmatrix}}}
Prisma rectangular ple d'amplada w, altura h, profunditat d, i massa m.
Prisma rectangular
I
=
[
1
12
m
(
h
2
+
d
2
)
0
0
0
1
12
m
(
w
2
+
d
2
)
0
0
0
1
12
m
(
w
2
+
h
2
)
]
{\displaystyle I={\begin{bmatrix}{\frac {1}{12}}m(h^{2}+d^{2})&0&0\\0&{\frac {1}{12}}m(w^{2}+d^{2})&0\\0&0&{\frac {1}{12}}m(w^{2}+h^{2})\end{bmatrix}}}
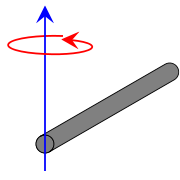
Vareta lineal orientada segons l'eix y, de longitud l , massa m i gruix despreciable, que gira respecte al seu extrem. Vareta lineal orientada segons l'eix y, de longitud l , massa m i gruix despreciable, que gira respecte al seu extrem.
I
=
[
1
3
m
l
2
0
0
0
0
0
0
0
1
3
m
l
2
]
{\displaystyle I={\begin{bmatrix}{\frac {1}{3}}ml^{2}&0&0\\0&0&0\\0&0&{\frac {1}{3}}ml^{2}\end{bmatrix}}}
Vareta lineal orientada segons l'eix y, de longitud l , massa m i gruix despreciable, que gire respecte el centre. Vareta lineal orientada segons l'eix y, de longitud l , massa m i gruix despreciable, que gire respecte el centre.
I
=
[
1
12
m
l
2
0
0
0
0
0
0
0
1
12
m
l
2
]
{\displaystyle I={\begin{bmatrix}{\frac {1}{12}}ml^{2}&0&0\\0&0&0\\0&0&{\frac {1}{12}}ml^{2}\end{bmatrix}}}
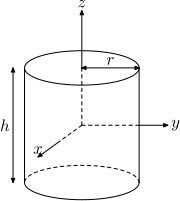
Cilindre sòlid de radi r , altura h i massa m .
I
=
[
1
12
m
(
3
r
2
+
h
2
)
0
0
0
1
12
m
(
3
r
2
+
h
2
)
0
0
0
1
2
m
r
2
]
{\displaystyle I={\begin{bmatrix}{\frac {1}{12}}m(3r^{2}+h^{2})&0&0\\0&{\frac {1}{12}}m(3r^{2}+h^{2})&0\\0&0&{\frac {1}{2}}mr^{2}\end{bmatrix}}}
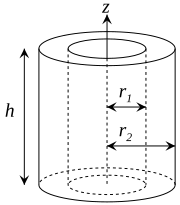
Escorça cilíndrica, amb radi interior r 1 , radi exterior r ₂, altura h i massa m .
I
=
[
1
12
m
(
3
(
r
1
2
+
r
2
2
)
+
h
2
)
0
0
0
1
12
m
(
3
(
r
1
2
+
r
2
2
)
+
h
2
)
0
0
0
1
2
m
(
r
1
2
+
r
2
2
)
]
{\displaystyle I={\begin{bmatrix}{\frac {1}{12}}m(3({r_{1}}^{2}+{r_{2}}^{2})+h^{2})&0&0\\0&{\frac {1}{12}}m(3({r_{1}}^{2}+{r_{2}}^{2})+h^{2})&0\\0&0&{\frac {1}{2}}m({r_{1}}^{2}+{r_{2}}^{2})\end{bmatrix}}}
Tanca
, 
...
, 
...
