From Wikipedia, the free encyclopedia
En ciències de la computació i matemàtiques un graf acíclic dirigit (o grafo acíclic dirigit ) conegut com a DAG per les seves sigles en anglès, és un graf dirigit que no té cicles; això significa que per a cada vèrtex v , no hi ha un camí directe que comenci i acabi en v . Els DAG apareixen en models on no té sentit que un vèrtex tingui un camí directe a ell mateix, per exemple, si un arc o → v indica que v és part de o , crear un cicle v → o indicaria que o és subconjunt de si mateix i de v , la qual cosa és impossible. Informalment un DAG "flueix" en només una direcció.
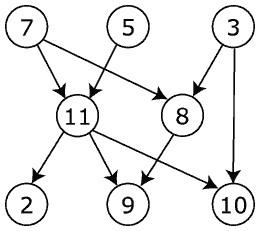
Cada DAG dona lloc a un ordenament parcial ≤ sobre els seus vèrtexs, on o ≤ v exactament quan hi ha un camí directe des de o a v . Molts DAG poden generar el mateix ordenament parcial dels vèrtexs sent el de menor nombre d'arcs anomenat la reducció transitiva i el que major nombre d'arcs la Cloenda transitiva. En particular, la clausura transitiva és l'ordre d'accessibilitat ≤ .
Una font és un vèrtex sense fluxos (relacions) d'entrada, mentre que un sifó és un vèrtex sense fluxos (relacions) de sortida.
Un DAG finit té com a mínim una font i un sifó.
La profunditat d'un vèrtex, en un DAG finit, és la longitud del camí més llarg que hi ha des d'una font a aquest vèrtex, l'alçada d'un vèrtex és la longitud més llarga del camí que hi hagi des del vèrtex a un sifó.
La longitud d'un DAG finit és la longitud (nombre d'arcs) del camí directe més llarg. Aquesta longitud és igual a la màxima alçada de totes les fonts i igual a la màxima profunditat de tots els sifons.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.