Električna mreža

Električne mreže su spojevi električnih elemenata kao što su otpornici, zavojnice i kondenzatori.

Jednostavno električno kolo

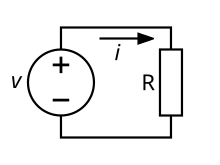
Električni ili strujni krug je takva mreža u kojoj zatvorena petlja omogućuje protjecanje struje. U najednostavnijem se obliku sastoji od izvora, vodiča i trošila.^[1]

Osnovni spojevi

Od početka su korišteni serijski, paralelni kao i kombinovani spoj:

Serijski spoj

Otpornik

Serijski spoj otpornika

Kod serijskog sklopa je ukupni napon suma napona pojedinačnih elemenata, napon na pojedinim elementima je proporcionalan njihovom otporu, kroz koje teče ista jačina struje.^[2]:

${\displaystyle R_{\mathrm {eq} }=R_{1}+R_{2}+\cdots +R_{n}}$

Kondenzator

Serijski spoj kondenzatora

Kod kondenzatora sabira se recipročna vrijednost kapaciteta odnosno saberu se električni naboji Q.^[3]

${\displaystyle Q=Q1+Q2+Q3+Q4...Qn={\frac {1}{C1}}+{\frac {1}{C2}}+{\frac {1}{C3}}+{\frac {1}{C4}}+...{\frac {1}{Cn}}}$ ukupni kapacitet je :${\displaystyle C={\frac {1}{Q}}}$

Zavojnica

Zavojnicne u serijskom spoju

Ukupan induktivitet dobija se sabirenjem induktivnih elemenata u spoju. Kroz induktivitete teče ista jačina struje.^[4]

${\displaystyle L_{\mathrm {eq} }=L_{1}+L_{2}+\cdots +L_{n}}$

Paralelni spoj

Paralelni spoj s otpornicima

Kod paralelnog spoja struja se dijeli na paralelne elemente, dok je napon svugdje isti isti.

Otpornik

Otpor se računa preko sume recipročnih vrijednosti pojedinih otpornika. Otpor se dobija sabiranjem recipročne vrijednosti pojedinih otpornika, u praksi se zove i vodljivost G:^[5]

${\displaystyle {\frac {1}{R_{\mathrm {eq} }}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}=G1+G2+....Gn}$ i tako se dobija :${\displaystyle R={1 \over G}}$

Kondenzator

Paralelni spoj kondenzatora

Kod paralelnog spoja kondenzatora sabiraju se kapaciteti.:^[6]:

${\displaystyle C_{\mathrm {eq} }=C_{1}+C_{2}+\cdots +C_{n}}$

Zavojnica

Paralelni sklop zavojnica

Induktivitet se računa preko sume recipročnih vrijednosti pojedinih zavojnica (induktiviteta).^[7] Recipročna vrijednost induktiviteta naziva se i reluktansa R^[8]:

${\displaystyle {\frac {1}{L_{\mathrm {eq} }}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}=R1+R2+....Rn}$ i tako se dobija :${\displaystyle L={1 \over R}}$

Kombinovani sklop

U analizi električnih mreža potrebno je odrediti struje i napone u krugu. Za mreže sastavljene od linearnih elemenata koristi se harmonijska analiza, pri čemu se sve veličine izražavaju kao kompleksni brojevi ovisni o frekvenciji.

Složene električne mreže

Složene električne mreže su mreže koje sadrže potrošače, prekidače, električne izvore struje, provodnike, kao i proste električne mreže. Za razliku od prostih električnih mreža, u složenim električnim mrežama dolazi do grananja električne struje.

Kao posljedica grananja električne struje, javljaju se topološke varijable. U ove varijable spadaju strujna čvorišta, strujne grane i konture.

• Čvor je dio složene električne mreže u kojoj dolazi do spajanja tri ili više elemenata.
• Grana je dio složene električne mreže sastavljen od serijski spojenih elemenata kroz koje teče ista struja (nalazi se između dva čvora).
• Kontura je dio složene električne mreže koji i sam predstavlja zatvoreni strujni krug, a sastoji se od najmanje dviju grana. Svaka kontura ima svoj smjer obilaženja koji je određen električnim varijablama kao što su napon i struja koja teče kroz električnu mrežu.

Metode analize složene električne mreže

Analizirati složenu električnu mrežu znači izračunati vrijednosti svih struja pod predpostavkom da je napon i otpor u električnoj mreži poznat.

Metoda Kirhofovih pravila

Analiza složene električne mreže metodom Kirhofovih pravila znači izračunati broj potrebnih jednačina za složenu električnu mrežu, zatim primjeniti prvo i drugi Kirhofovo pravilo u električnu mrežu. Broj jednačina potrebno za analizu složene mreže je jednaku broju strujnih grana iste.

Broj jednačina koji će se pisati prvim Kirhofovim pravilom je jednak broju čvorova u električnoj mreži manje jedan, dok je broj jednačina koji će se pisati drugim Kirhofovim pravilom jednak broju ukupno-potrebnih jednačina, odnosno grana, manje broj čvorova više jedan.

Metoda konturnih struja

Analizom složene električne mreže metodom konturnih struja će se koristiti broj jednačina koji bi bio jednak primjenom drugog Kirhofovog pravila. Opšta jednačina za metod konturnih struja:

${\displaystyle U_{I}=R_{11}\times I_{I}+R_{12}\times I_{II}}$

${\displaystyle U_{II}=R_{21}\times I_{I}+R_{22}\times I_{II}}$

Gdje je:

• ${\displaystyle U_{I}}$ - Zbir svih napona u prvoj konturi
• ${\displaystyle U_{II}}$ - Zbir svih napona u drugoj konturi
• ${\displaystyle R_{11}}$ - Zbir svih otpora u prvoj konturi
• ${\displaystyle R_{22}}$ - Zbir svih otpora u drugoj konturi
• ${\displaystyle R_{12}}$ / ${\displaystyle R_{21}}$- Otpori koji pripadaju prvoj i drugoj konturi

Metoda napona čvorova

Analiza složene električne mreže metodom napona čvorova, uzemljit ćemo jedan od čvorova tako da je njegov potencijal jednak nuli. Na osnovu uzemljenog čvora, traži se potencijal preostalih čvorova pa se tako struje između čvorova izračunavaju primjenom Ohmovog zakona.

Kao posljedica uzemljenja čvora, koristit će se samo jedna jednačina:

${\displaystyle I_{I}=G_{11}\times V_{1}}$

Gdje je:

• ${\displaystyle I_{I}}$ - Omov zakon za napone svih grana
• ${\displaystyle G_{11}}$ - Recipročna vrijednost zbira otpora u svakoj grani pojedinačno
• ${\displaystyle V_{1}}$ (φ) - Električni potencijal

Nakon izračunavanja ${\displaystyle I_{I}}$ i ${\displaystyle G_{11}}$, slijedi da je struja koja teče kroz prvu granu jednaka omjeru razlike napona prve grane, elekričnog potencijala i otpora u prvoj grani. Struja koja teče kroz drugu granu je jednaka omjeru razlike napona prve grane, električnog potencijala i otpora u drugoj grani dok je struja koja teče kroz treću granu jednaka omjeru električnog potencijala i otpora u trećoj grani.

Metoda ukupnog otpora

Još nazvana i Medićeva metoda, analiza složene električne mreže ovom metodom znači zamjeniti sve otpore u strujnoj grani sa jednim otporom. Nakon toga ukupni otpori se svrstavaju u razlomke, koji se sabiru ili množe nakon čega se dobiva vrijednost struja.

Reference

1. GrundschaltungenElektronik Kompendium, pristupljeno 20.8.2015 (de)
2. Reihenschaltung von WiderständenElektronik Kompendium, pristupljeno 20.8.2015 (de)
3. Reihenschaltung von KondensatorenElektronik Kompendium, pristupljeno 20.8.2015 (de)
4. Reihenschaltung von InduktivitätenElektrotechnik Fachwissen , pristupljeno 21.8.2015 (de)
5. Parallelschaltung von WiderständenElektronik Kompendium, pristupljeno 21.8.2015 (de)
6. Parallelschaltung von KondensatorenElektronik Kompendium, pristupljeno 21.8.2015 (de)
7. Parallelschaltung von InduktivitätenElektrotechnik Fachwissen, pristupljeno 21.8.2015 (de)
8. ReluktanzWissen, pristupljeno 21.8.2015 (de)

Vanjski linkovi

• FET Fakultet elektrotehnike Tuzla^{[mrtav link]}
• e-learning Univerzitet u Frankfurtu (de)