জ্যোতির্বিজ্ঞান ও বিশ্বতত্ত্বে তমোপদার্থ, গুপ্ত পদার্থ বা অদৃশ্য পদার্থ (ডার্ক ম্যাটার নামেও পরিচিত) এক ধরনের অনুকল্পিত (hypothesized) পদার্থ যার প্রকৃতি এখন পর্যন্ত জানা সম্ভব হয়নি। অন্য পদার্থের সাথে এরা কেবল মহাকর্ষ বলের মাধ্যমে ক্রিয়া করে বলে ধারণা করা হয়; সে হিসেবে এদেরকে শনাক্ত করার একমাত্র উপায় এদের মহাকর্ষীয় প্রভাব। মনে করা হয়, মহাবিশ্বের মোট ভরের পাঁচ ভাগের চার ভাগের জন্যই দায়ী তমোপদার্থ। এরা তড়িচ্চুম্বকীয় তরঙ্গ (যেমন, আলো) নিঃসরণ বা শোষণ কোনটাই করে না, এমনকি এরা এসব তরঙ্গের সাথে কোন ধরনের মিথস্ক্রিয়াই করে না, তাই দূরবীন দিয়ে এদের সরাসরি দেখার কোন উপায় নেই।[১] ধারণা করা হয় তমোপদার্থ মহাবিশ্বের মোট পদার্থের ৮৩% এবং মোট ভর-শক্তির ২৩%।[২]
তমোপদার্থ প্রথম মনোযোগ আকর্ষণ করেছিল ভর গণনায় একটি অসামঞ্জস্যের কারণে। বিজ্ঞানীরা দুইভাবে আমাদের ছায়াপথের ভর নির্ণয় করেছিলেন: মহাকর্ষের প্রভাবে তারাগুলো ছায়াপথের কেন্দ্রকে আবর্তন করে, এই আবর্তন অনুসরণ করে প্রকৃত ভর নির্ণয় করা হয়, এর পাশাপাশি প্রতিটি তারা এবং গ্যাসপিণ্ডের নিজস্ব ভর যোগ করে সমগ্র ছায়াপথে দৃশ্যমান বা উজ্জ্বল পদার্থের ভর নির্ণয় করা হয়। দেখা যায় প্রকৃত ভর দৃশ্যমান ভরের চেয়ে অনেক বেশি। ১৯৩২ সালে ইয়ান ওর্ট আকাশগঙ্গার মধ্যকার তারাগুলোর কক্ষীয় বেগ ব্যাখ্যার জন্য এবং ১৯৩৩ সালে ফ্রিৎস জুইকি ছায়াপথ স্তবকে ছায়াপথগুলোর কক্ষীয় বেগ ব্যাখ্যার জন্য এই বাড়তি ভরের প্রয়োজনীয়তা উল্লেখ করেছিলেন। এরপর তমোপদার্থের উপস্থিতির পক্ষে আরও অনেক ধরনের পর্যবেক্ষণমূলক প্রমাণ পাওয়া যেতে থাকে। যেমন: ছায়াপথের ঘূর্ণন বেগ, বুলেট স্তবকের মত ছায়াপথ স্তবকের কারণে পটভূমির বস্তুর মহাকর্ষীয় লেন্সিং এবং ছায়াপথ ও ছায়াপথ স্তবকের উত্তপ্ত গ্যাসের তাপমাত্রা বণ্টন। বিশ্বতত্ত্ববিদরা মনে করেন, তমোপদার্থ এমন কিছু অতি-আণবিক কণা দিয়ে গঠিত যা মানুষ এখনও আবিষ্কার করতে পারেনি।[৩][৪]
তমোপদার্থ গঠনকারী এই অতি-আণবিক কণাগুলো আবিষ্কার করা বর্তমানে কণা পদার্থবিজ্ঞানের একটি অন্যতম বৃহৎ গবেষণা ক্ষেত্র।[৫] অন্যদিকে আমাদের সৌরজগতে এমনকি আমাদের আশেপাশেই প্রচুর তমোপদার্থ আছে ধরে নিয়ে বিজ্ঞানীরা ভূগর্ভস্থ পরীক্ষাগারে এদের শনাক্ত করার চেষ্টাও চালিয়ে যাচ্ছেন। অবশ্য ২০১২ সালের এপ্রিলে ইউরোপিয়ান সাউদার্ন অবজারভেটরির একটি পরীক্ষায় দেখা গেছে আমাদের প্রতিবেশী প্রায় ৪০০টি তারা এমন আচরণ করছে যেন কোন তমোপদার্থ নেই। এটি সত্যি হলে ভূগর্ভস্থ পরীক্ষাগুলোর ভবিষ্যৎ হুমকির সম্মুখীন হবে।[৬] অধিকাংশ জ্যোতির্বিজ্ঞানী তমোপদার্থ আছে এবং ভবিষ্যতে এটা আবিষ্কৃত হবে মনে করলেও অনেকে আবার বিকল্প কিছু তত্ত্ব সমর্থন করেন। মহাকর্ষের যে নীতির কারণে তমোপদার্থ অবতারণার প্রয়োজন পড়ে স্বয়ং সেই নীতিকেই বিশেষ ক্ষেত্রে সংশোধনের পরামর্শ দিয়েছেন অনেকে।[৭]
তমোপদার্থ গবেষণার ইতিহাস
কোন অদৃশ্য পদার্থকে তার মহাকর্ষীয় প্রভাবের মাধ্যমে প্রথম শনাক্ত করা হয়েছিল ১৮০১ সালে। সে বছর ফ্রিডরিশ ভিলহেল্ম বেসেল ঘোষণা করেন যে, লুব্ধক ও প্রসিয়ন তারা দুটির অবস্থান কয়েক দশক ধরে পরিমাপ করার পর মনে হচ্ছে তাদের দুজনেরই একটি করে সঙ্গী তারা রয়েছে যাদের ভর আবার তাদের ভরের সমতুল্য। ১৮৬২ সালে অবশ্য এই অদৃশ্য ভর আর অদৃশ্য থাকেনি, তখন আরেক জ্যোতির্বিজ্ঞানী অ্যালান জি ক্লার্ক দেখতে পান যে লুব্ধকের একটি সঙ্গী তারা রয়েছে, নাম লুব্ধক (সিরিয়াস) বি। লুব্ধক ও লুব্ধক বি একে অপরকে আবর্তন করছে। তবে সেকালের সেই অদৃশ্য পদার্থ আসলে তমোপদার্থ নয়, আমাদের পর্যবেক্ষণ পদ্ধতি যথেষ্ট উন্নত না হওয়ায় আমরা তাদের দেখতে পারিনি কেবল। তমোপদার্থ একেবারে অন্যরকম।
বেসেল ও ক্লার্কের কয়েক প্রজন্ম পর ঊনবিংশ শতকের প্রথমার্ধে পরপর দুটি পর্যবেক্ষণ অন্য ধরনের কিছু অদৃশ্য পদার্থের আভাস দিতে শুরু করে। প্রথমে, ইয়ান ওর্ট সূর্যের প্রতিবেশী তারার সংখ্যা, অবস্থান ও গতিবেগ নির্ণয় করে সেই বেগ থেকে ভর নির্ণয় করেন যাকে বলা যায় মহাকর্ষীয় ভর। কিন্তু লক্ষ্য করেন, সবগুলো তারার ভরের যোগফল এই মহাকর্ষীয় ভরের অর্ধেক বা তারও কম। এরপর ১৯৩৩ সালে বেতার জ্যোতির্বিজ্ঞানী ফ্রিৎস জুইকি ছায়াপথ স্তবকের ভিন্ন ভিন্ন ছায়াপথের বিচ্ছুরণ বেগ নির্ণয় করে একইভাবে তা থেকে স্তবকের মোট ভর নির্ণয় করেন। তিনিও অবাক হয়ে লক্ষ্য করেন যে, এত অধিক বেগের ছায়াপথগুলোকে স্তবকের মাঝে ধরে রাখতে হলে সেখানে দৃশ্যমান ভরের চেয়ে ১০ থেকে ১০০ গুণ বেশি ভর থাকা প্রয়োজন। দুটি ফলাফলই তমোপদার্থের ইঙ্গিত দিলেও সে সময় জুইকির তুলনায় ওর্টের গবেষণা বেশি স্বীকৃতি লাভ করেছিল।
এর পরের দশকগুলোতেও এ বিষয়ক গবেষণা চলতে থাকে। তবে তমোপদার্থ গবেষণার আধুনিক যুগ শুরু হয় ১৯৭০-এর দশকে। ১৯৭৪ সালে একদিকে জিম পিবলস, জেরেমায়াহ ওস্ট্রাইকার ও এ ইয়াহিল এবং অন্যদিকে Einasto, Kraasik ও Saar অনেকগুলো ছায়াপথের ব্যাসার্ধভিত্তিক ভর নির্ণয় করেন। অর্থাৎ ছায়াপথের কেন্দ্র থেকে বিভিন্ন ব্যাসার্ধ্য পর্যন্ত মোট ভরের পরিমাণ তালিকাবদ্ধ করেন। তারা দেখতে পান কেন্দ্র থেকে প্রায় ১০০ কিলোপারসেক পর্যন্ত ভর রৈখিকভাবে বৃদ্ধি পায় এবং সাধারণ সর্পিলাকার ও উপবৃত্তীয় ছায়াপথের মোট ভর আনুমানিক ১০১২সৌর ভর। তখন থেকেই তমোপদার্থের ধারণাটি বিজ্ঞানী মহলে বিপুল জনপ্রিয়তা পেতে শুরু করে।[১]
এর আগে ১৯৫৯ সালে লুইস ভোল্ডার্স দেখিয়েছিলেন যে ত্রিকোণ মণ্ডলে অবস্থিত এম৩৩ নামক সর্পিলাকার ছায়াপথের ঘূর্ণন কেপলারীয় গতিবিদ্যা দিয়ে ব্যাখ্যা করা যায় না।[৮] এই গবেষণা অনুসরণ করে ১৯৬০-এর দশকের শেষদিকে ও ১৯৭০-এর দশকের শুরুতে তরুণ মার্কিন জ্যোতির্বিজ্ঞানী ভেরা রুবিন সে সময়কার সবচেয়ে উন্নত স্পেকট্রোগ্রাফ দিয়ে কিছু সর্পিলাকার ছায়াপথের ঘূর্ণন চক্র তৈরি করেন। অর্থাৎ তিনি বিভিন্ন ছায়াপথের ব্যাসার্ধ্যের সাপেক্ষে ঘূর্ণন বেগের পরিমাণ একটি লেখচিত্রে অঙ্কন করেন।[৯] তিনি অবাক হয়ে লক্ষ্য করেন যে, বেগের বক্ররেখাটি নিউটনের মহাকর্ষ সূত্র অনুসারে যেমন নিচের দিকে নেমে যাওয়ার কথা ছিল তেমন হচ্ছে না। তাই ১৯৭৫ সালে অ্যামেরিকান অ্যাস্ট্রোনমিক্যাল সোসাইটির মিটিংয়ে তিনি ঘোষণা করেন যে সর্পিলাকার ছায়াপথের অধিকাংশ তারার বেগ ধ্রুব থাকে। ১৯৭৮ সালে তার এই ফলাফল আরেকজন বিজ্ঞানী সত্য প্রমাণ করেন।[১০] অবশেষে ১৯৮০ সালে একটি অত্যন্ত প্রভাবশালী গবেষণাপত্রে রুবিন তার পরিপূর্ণ ফলাফল প্রকাশ করেন। তার ফলাফলের অর্থ দাঁড়ায়, হয় নিউটনের মহাকর্ষ সূত্র বিশেষ কিছু ক্ষেত্রে সঠিক নয়, নয়তো ছায়াপথের মোট ভরের একটি বিশাল অংশ গুপ্ত অবস্থায় আছে।[১১] এভাবেই প্রোথিত হয় তমোপদার্থের শক্ত ভিত্তি। তমোপদার্থের উপস্থিতির পর্যবেক্ষণমূলক প্রমাণ অংশে এই পর্যবেক্ষণের বৈজ্ঞানিক ভিত্তি নিয়ে বিস্তারিত আলোচনা করা হবে।
পর্যবেক্ষণমূলক প্রমাণ
ফ্রিৎস জুইকি কোমা স্তবকে ভিরিয়াল উপপাদ্য প্রয়োগ করে বুঝতে পেরেছিলেন যে মোট ভরের বিশাল একটা অংশ দেখা যাচ্ছে না। তিনি স্তবকের প্রান্তের দিকে অবস্থিত ছায়াপথগুলোর গতিবেগ থেকে মোট ভর নির্ণয় করেন, তারপর এই ভরকে তুলনা করেন মোট ছায়াপথের সংখ্যা ও স্তবকের সার্বিক উজ্জ্বলতা থেকে প্রাপ্ত ভরের সাথে তুলনা করে দেখেন,পর্যবেক্ষণযোগ্য ভরের তুলনায় ৪০০ গুণ বেশি ভর স্তবকটিতে থাকার কথা। প্রান্তের ছায়াপথগুলোর বেগ এতো বেশি যে দৃশ্যমান পদার্থের মহাকর্ষ বল দিয়ে তা ব্যাখ্যা করা যায় না। অন্য কথায়, স্তবকের মহাকর্ষ বল ছায়াপথগুলোকে ধরে রাখার জন্য যথেষ্ট নয়। সেই থেকে জুইকি অনুমান করেন যে অনেক পদার্থ অদৃশ্য বা গুপ্ত অবস্থায় আছে।[১২] পরবর্তীতে এর পক্ষে আরও অনেক পর্যবেক্ষণমূলক প্রমাণ পাওয়া গেছে।
ছায়াপথের ঘূর্ণন বক্র
তমোপদার্থের পক্ষে সবচেয়ে শক্তিশালী প্রমাণ এসেছে সর্পিল ছায়াপথ থেকে। এ ধরনের ছায়াপথের তারাগুলো বণ্টিত থাকে কেন্দ্রে অবস্থিত একটি গোলকাকার বাল্জ এবং একটি সরু চাকতিতে। বাল্জের পরই চাকতি শুরু হয়। ছায়াপথের মধ্যকার তারা এবং গ্যাসের কক্ষীয় আবর্তন বেগ তাদের থেকে আসা তড়িচ্চুম্বকীয় বিকিরণের ডপলার সরণ থেকে নির্ণয় করা যায়। কেন্দ্র থেকে বিভিন্ন ব্যাসার্ধ্যে অবস্থিত গ্যাসের গতিবেগ নির্ণয় করে ব্যাসার্ধ্য বনাম বেগের একটি লেখচিত্র আঁকা সম্ভব যাকে বলা হয় ছায়াপথের ঘূর্ণন বক্র। চাকতিতে সাধারণত প্রচুর নিরপেক্ষ হাইড্রোজেন গ্যাস থাকে এবং তাদের বিস্তৃতি তারার চেয়ে অনেক দূর পর্যন্ত। উপরন্তু এসব গ্যাস থেকে আসা ২১ সেন্টিমিটার তরঙ্গদৈর্ঘ্যের বেতার তরঙ্গের ডপলার সরণ থেকে তাদের বেগ নির্ণয় সম্ভব। এজন্যই ঘূর্ণন বেগের লেখচিত্র আঁকার জন্য অনেক সময়ই নিরপেক্ষ হাইড্রোজেন গ্যাস ব্যবহার করা হয়।
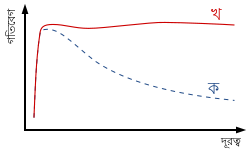
এমন একটি ঘূর্ণন লেখ পাশের চিত্রে দেখানো হয়েছে। সকল সর্পিলাকার ছায়াপথের ঘূর্ণন বক্রই এমন হয়। লেখ থেকে দেখা যাচ্ছে, গ্যাসের কক্ষীয় বেগ কেন্দ্র থেকে বাইরের দিকে বাড়তে থাকে এবং একটি নির্দিষ্ট বেগে পৌঁছুনোর পর আর পরিবর্তিত হয় না। এমনকি অনেক দূর পর্যন্তও সকল বস্তুকে একই বেগে আবর্তিত হতে দেখা যায়। ১৯৭০ সালেই কেন ফ্রিম্যান এমন ঘূর্ণন বক্র তৈরি করতে সমর্থ হয়েছিলেন।[১৩] এটি সম্পূর্ণ অনাকাঙ্ক্ষিত ছিল। কারণ ছায়াপথের চাকতির উজ্জ্বলতা কেন্দ্র থেকে যত বাইরের দিকে যাওয়া যায় তত কমতে থাকে। অর্থাৎ অধিকাংশ তারা এবং সেহেতু দৃশ্যমান ভর কেন্দ্রের কাছাকাছি একটি অঞ্চলে ঘনীভূত। ব্যাসার্ধ্যের সাথে সাথে পদার্থের পরিমাণ কমতে থাকে। কেপলারীয় ঘূর্ণনের ক্ষেত্রে নিউটনের মহাকর্ষ সূত্র অনুসারে আমরা জানি,
যেখানে v ঘূর্ণন বেগ, G মহাকর্ষীয় ধ্রুবক, M ছায়াপথের মোট ভর এবং r ব্যাসার্ধ্য। সূত্র থেকে দেখা যাচ্ছে ব্যাসার্ধ্য বাড়লে বেগ কমতে থাকার কথা। এই সূত্র বাল্জের ক্ষেত্রে প্রযোজ্য হবে না, কারণ সেখানে কেপলারীয় ঘূর্ণনের তুলনায় তারা এবং গ্যাসের বেগের বিচ্ছুরণ বেশি প্রভাবশালী। তাই লেখচিত্রের প্রথম অংশে ব্যাসার্ধ্যের সাথে বাড়তে থাকে। যে ব্যাসার্ধ্যে বেগ ধ্রুব হয় সেখান থেকে কেপলারীয় গতি প্রযোজ্য। তাই হিসেব মতে সেখান থেকে ব্যাসার্ধ্যের সাথে সাথে বেগ কমার কথা যা নীল ড্যাশ রেখাটি দিয়ে দেখানো হয়েছে। অর্থাৎ এই সূত্র অনুযায়ী একটি লেখচিত্র আঁকলে তা নীল রেখাটির মত হতো। কিন্তু পর্যবেক্ষণে পাওয়া যায় লাল রেখাটি, অর্থাৎ বেগ কমে না। সূত্র থেকে আরও দেখা যাচ্ছে ছায়াপথের মোট ভর M যদি বাড়ানো হয় তাহলে বেগ বেড়ে যায়। সুতরাং নীলের বদলে লাল রেখাটি পাওয়ার একটি উপায় হচ্ছে ভর বৃদ্ধি, অর্থাৎ প্রয়োজন অতিরিক্ত ভরের। এই অতিরিক্ত ভরই তমোপদার্থ।
ঠিক কতটুকু অতিরিক্ত ভর থাকলে লাল রেখা পাওয়া যাবে সেটা সহজেই পরিমাপ করা সম্ভব। সেটা করেই দেখা গেছে তমোপদার্থের পরিমাণ দৃশ্যমান পদার্থের তুলনায় অনেক বেশি। বেগ ধ্রুব রাখার জন্য ব্যাসার্ধ্যের সাথে সাথে উক্ত ব্যাসার্ধ্যের ভেতর অবস্থিত মোট তমোপদার্থের পরিমাণ বাড়তে হবে। উপরের সূত্র থেকেই দেখা যাচ্ছে v ধ্রুব রাখতে হলে,
হতে হবে যেখানে হচ্ছে ব্যাসার্ধ্যের ভেতর অবস্থিত তমোপদার্থের মোট ভর। পরোক্ষ উপায়ে তমোপদার্থ শনাক্ত করার জন্য আকাশগঙ্গা সবচেয়ে উপযুক্ত মাধ্যম। আকাশগঙ্গার ঘূর্ণন লেখ আঁকলে দেখা যায়, চাকতির প্রায় সকল তারার বেগ সেকেন্ডে আনুমানিক ২২০ কিলোমিটার।[১৪]
ছায়াপথে বেগের বিচ্ছুরণ
সর্পিলাকার ছায়াপথের ক্ষেত্রে তারা এবং গ্যাসের আবর্তন বেগের মাধ্যমে ঘূর্ণন বক্র তৈরি করা হয়। কিন্তু উপবৃত্তীয় ছায়াপথের ক্ষেত্রে আবর্তন বেগের বদলে বেগের বিচ্ছুরণ পরিমাপ বেশি কার্যকরী। পুরো উপবৃত্তীয় ছায়াপথকে তুলনা করা যেতে সর্পিলাকার ছায়াপথের বাল্জের সাথে। বাল্জে আবর্তন বেগের তুলনায় বিচ্ছুরণ বেগ বেশি প্রভাবশালী, আর উপবৃত্তীয় ছায়াপথের পুরোটাতেই বেগের বিচ্ছুরণ অনেক বেশি প্রভাবশালী। তারা এবং গ্যাসের বর্ণালীতে যেসব নিঃসরণ বা বিশোষণ রেখা পাওয়া যায় তাদের প্রস্থ পরিমাপের মাধ্যমে বিচ্ছুরণ নির্ণয় করা হয়।[১৫] বিচ্ছুরণ আসলে একটি গড় বেগের সাথে বিভিন্ন বস্তুর বেগের পার্থক্য বোঝায়। যেমন একটি তারা স্তবকের সকল তারার গড় বেগের সাথে প্রতিটি তারার বেগের পার্থক্য হচ্ছে বিচ্ছুরণ। দুটি তারার বেগ যথাক্রমে ১০০ ও ৪০০ কিমি/সে হলে গড় বেগ ২৫০ কিমি/সে এবং বেগের বিচ্ছুরণ ১৫০ কিমি/সে।
বেগের বিচ্ছুরণ জানা থাকলে ভিরিয়াল উপপাদ্যের মাধ্যমে সহজেই ছায়াপথটির ভর পরিমাপ করা যায়। পাশাপাশি নির্ণয় করা হয় ছায়াপথটির দীপন ক্ষমতা। এই দুটি রাশির অনুপাতকে বলে ভর-আলো অনুপাত যার আদর্শ একক হচ্ছে কেজি/ওয়াট। যেমন, সূর্যের ভর-আলো অনুপাত ৫১৩৩ কেজি/ওয়াট। আসলে সকল বস্তুর ভর-আলো অনুপাতকে সূর্যের সাপেক্ষে প্রকাশ করা হয়। কোন ছায়াপথের ভর-আলো অনুপাত ১০ বলার অর্থ হচ্ছে তার ভর-আলো অনুপাত সূর্যের তুলনায় ১০ গুণ বেশি। এই অনুপাত ১ এর বেশি হওয়ার অর্থই হচ্ছে সেখানে অদৃশ্য ভর আছে। সাধারণ অর্থে, বেগের বিচ্ছুরণ যত বেশি তার ভর তত বেশি, যথারীতি ভর-আলো অনুপাত তত বেশি এবং সেথায় তমোপদার্থও তত বেশি।[১৬]
উপবৃত্তীয় ছায়াপথ যেহেতু চাকতিবিশিষ্ট ছায়াপথের সাংঘর্ষিক মিলনের মাধ্যমে গঠিত হয় সেহেতু তারাও তমোপদার্থের হেলোতে প্রোথিত থাকবে বলে ধারণা করা হয়েছিল। এবং বাস্তবেও বেশ কিছু দানবীয় উপবৃত্তাকার ছায়াপথের এক্স-রশ্মি এবং মহাকর্ষীয় লেন্সিং পর্যবেক্ষণ করে তমোপদার্থের দেখা মিলেছে। কিন্তু সাধারণ উপবৃত্তীয় ছায়াপথের বেগের বিচ্ছুরণ থেকে পাওয়া ঘূর্ণন বক্র তমোপদার্থের মডেলের সাথে খাপ খাচ্ছিল না। দেখা যাচ্ছিল তাদের ক্ষেত্রে তারাদের বেগ প্রান্তের দিকে আসলেই কমতে থাকে। তাই একে তমোপদার্থের বিরুদ্ধে প্রমাণ হিসেবে দেখানো হয়েছিল। কিন্তু পরবর্তীতে দেখা গেছে পাশ দিয়ে অতিক্রম করে যাওয়া একটি ছায়াপথের আকর্ষণে এসব প্রান্তিক তারা তাদের ছায়াপথ থেকে বেরিয়ে পড়েছিল যে কারণে তাদের কক্ষপথ অনেক লম্বা হয়ে গেছে ও বেগ আগের চেয়ে কমে গেছে। সিম্যুলেশনে দেখা গেছে তমোপদার্থের হেলোর মধ্যেও এমন স্বল্প বেগের প্রান্তিক তারাবিশিষ্ট উপবৃত্তাকার ছায়াপথ গঠিত হওয়া সম্ভব।[১৭]
মহাবিশ্বের ঘনত্ব
মহাবিশ্বের বিভিন্ন উপাদানের ঘনত্বকে একটি ক্রান্তীয় ঘনত্বের সাপেক্ষে প্রকাশ করা হয়। কোন পদার্থের ঘনত্বকে ক্রান্তীয় ঘনত্ব দিয়ে ভাগ করলে যা পাওয়া তাকে বলা হয় ঘনত্ব রাশি, একে প্রকাশ করা হয় গ্রিক ওমেগা অক্ষরটি দিয়ে। যেমন মহাবিশ্বের মোট পদার্থের ঘনত্বকে ক্রান্তীয় ঘনত্ব দিয়ে ভাগ করলে যে রাশি পাওয়া যায় তাকে বলা হয়, আর মোট দৃশ্যমান বা উজ্জ্বল পদার্থকে ক্রান্তীয়টি দিয়ে ভাগ করলে পাওয়া যায়। এই ওমেগা রাশি আবার মহাবিশ্বের আকৃতি ও তথাপি পরিণতি নির্ধারণ করে।এর মান ১-এর কম হলে মহাবিশ্বের বক্রতা ঋণাত্মক এবং সেটি মুক্ত, ১-এর বেশি হলে বক্রতা ও ধনাত্মক ও মহাবিশ্ব বদ্ধ, আর ১-এর সমান হলে কোন বক্রতা নেই অর্থাৎ মহাবিশ্ব সমতল বা ইউক্লিডীয়। মহাবিশ্বের মোট উজ্জ্বল পদার্থের ঘনত্বকে ক্রান্তীয় ঘনত্ব দিয়ে ভাগ করে দেখা গেছে,
- যেখানেএবং= বর্তমানের হাবল ধ্রুবক
স্পষ্টতই কেবল দৃশ্যমান পদার্থ ধরলে ওমেগার মান ১-এর চেয়ে অনেক কম তথা মহাবিশ্বের ঘনত্ব ক্রান্তীয় ঘনত্বের চেয়ে অনেক কম। কিন্তু অনেক পরীক্ষা থেকেই জানা গেছে মহাবিশ্বে সামগ্রিক বক্রতা বর্তমানে শূন্যের কাছাকাছি, অর্থাৎ মহাবিশ্ব প্রায় সমতল। অন্য কথায় ওমেগা রাশির মান ১ এর খুব কাছাকাছি। একমাত্র তমোপদার্থের অস্তিত্ব থাকলেই ওমেগার মান বৃদ্ধি পেয়ে এমন হতে পারে। ছায়াপথ তমোপদার্থের বিশাল হেলোর মধ্যে প্রোথিত আছে ধরে নিলে ছায়াপথের গড় ভর-আলো অনুপাত পাওয়া যায় প্রায় ৩০। সে হিসেবে ওমেগার মান গিয়ে দাঁড়ায় ০.০৩ থেকে ০.০৫। তবে এই পরিমাপেও তমোপদার্থের পরিমাণ অনেক কম ধরা হয়েছে। উপ-ছায়াপথগুলোর গতি পর্যবেক্ষণ করে তমোপদার্থের যে পরিমাণ জানা গেছে তা অনুসারে ওমেগার মান ০.২ থেকে ০.৫ পর্যন্ত পৌঁছায়।[১৪]
ছায়াপথ স্তবক
ছায়াপথ স্তবকে কয়েক শত থেকে কয়েক হাজার ছায়াপথ এবং ছায়াপথগুলোর মধ্যবর্তী স্থান তথা আন্তঃছায়াপথীয় মাধ্যমে প্রচণ্ড উত্তপ্ত গ্যাস থাকে। এই উত্তপ্ত গ্যাস এক্স-রশ্মি নিঃসরণ করে। মহাকাশে স্থাপিত এক্স-রশ্মি দুরবিন দিয়ে জানা গেছে স্তবকের এই গ্যাসের মোট ভর সকল ছায়াপথের ভরের তুলনায় প্রায় ১০ গুণ। ওদিকে আবার শনাক্তকৃত এক্স-রশ্মির মাধ্যমে গ্যাসের তাপমাত্রা ও ঘনত্ব নির্ণয় করা যায়। আর ঘনত্ব ও তাপমাত্রা জানা থাকলে উদস্থিতিসাম্যের সমীকরণ দিয়ে স্তবকের মোট ভর (তমোপদার্থসহ) বের করা যায়। সেটি করে দেখা গেছে তমোপদার্থের ভর গ্যাসের মোট ভরেরও ১০ গুণ।[১৮]এবেল ২০২৯ স্তবকের এক্স-রশ্মি নিঃসরণকারী গ্যাসের তাপমাত্রা ও উজ্জ্বলতা পর্যবেক্ষণ করে বিজ্ঞানীরা স্তবকে তমোপদার্থের একটি বিস্তারিত মানচিত্র তৈরি করতে সক্ষম হয়েছেন। মানচিত্র থেকে দেখা গেছে তমোপদার্থের ঘনত্ব কেন্দ্রের দিকে ক্রমান্বয়ে বাড়তে থাকে এবং কেন্দ্রীয় ছায়াপথটির কাছে সর্বোচ্চ মানে পৌঁছায়।[১৯]

এছাড়া ছায়াপথ স্তবকের ভিন্ন ভিন্ন ছায়াপথের ঘূর্ণন বেগ থেকে ছায়াপথের মোট ভরের একটি ধারণা পাওয়া যায়। ডার্ক ম্যাটার নামটি যারা প্রথম ব্যবহার করেছিলেন তাদের একজন ফ্রিৎস জুইকি। জুইকি নিজেও এই প্রক্রিয়ায় প্রথমে স্তবকের ভর নির্ণয় করে অসঙ্গতি টের পেয়েছিলেন। ঘূর্ণন বেগ থেকে ভরের সাথে তিনি ছায়াপথের উজ্জ্বলতা থেকে অনুমানকৃত ভরের তুলনা করে বুঝতে পারেন যে, অনেক বেশি ভর লুক্কায়িত আছে। তবে তিনি জানতেন যে এই দুটি প্রক্রিয়ারই অনেক সীমাবদ্ধতা আছে। এজন্য ১৯৩৭ সালে প্রকাশিত একটি গবেষণাপত্রে জুইকি ছায়াপথ স্তবকের ভর নির্ণয়ের আরও উন্নত তিনটি পদ্ধতি প্রস্তাব করেন এবং তিন পদ্ধতিতেই কোমা স্তবকের ভর নির্ণয় করে সেগুলো তুলনা করেন। প্রথমত তিনি ভিরিয়াল উপপাদ্যের মাধ্যমে কোমা স্তবকের ভর নির্ণয় করে সেটাকে মোট উজ্জ্বলতার সাথে তুলনা করেন। তার প্রাথমিক হিসাবে কোমা স্তবকের ভর-আলো অনুপাত হয় প্রায় ৫০০, অর্থাৎ বিপুল পরিমাণ পদার্থ ধরা-ছোয়ার বাইরে। অবশ্য স্তবকটিকে স্থিতিশীল ধরে না নিয়ে আবার ভিরিয়াল উপপাদ্য প্রয়োগ করেন এবং সেক্ষেত্রে ভর-আলো অনুপাত বেশ কম পাওয়া যায়। তারপরও ব্যত্যয় রয়ে গিয়েছিল।
সেই ১৯৩০-এর দশকেই জুইকি বুঝতে পেরেছিলেন যে স্তবকের ভর নির্ণয়ের সবচেয়ে কার্যকরী উপায় হবে মহাকর্ষীয় লেন্সিং। আইনস্টাইনের সাধারণ আপেক্ষিকতা অনুসারে পটভূমির কোন বস্তু থেকে আসা আলো পুরোভূমির আরেকটি বস্তুর মহাকর্ষ বলের কারণে বেঁকে যায়। এই বেঁকে যাওয়ার পরিমাণ নির্ণয়ের মাধ্যমে পুরোভূমির বস্তুটির ভর নির্ণয় করা সম্ভব। এ ধরনের লেন্সিং এর প্রকৃত নাম সবল মহাকর্ষীয় লেন্সিং। এক্ষেত্রে সমীকরণটি হচ্ছে:
- যেখানেবেঁকে যাওয়ার পরিমাণ, M পুরোভূমির বস্তুর ভর এবং r পুরোভূমির বস্তু থেকে আলোকরশ্মির দূরত্ব
এই পদ্ধতিতে বর্তমানে ছায়াপথ স্তবকের সবচেয়ে নিখুঁত ভর নির্ণয় করা হয়। আর এটি মূলত তমোপদার্থের ভর। কারণ লেন্সিং ঘটে কেবল মহাকর্ষ বলের কারণে আর তমোপদার্থের ভর অনেক বেশি হওয়ায় লেন্সিং এ তার অবদানই সবচেয়ে বেশি। তমোপদার্থের কারণে পটভূমির বস্তু থেকে আসা আলো বিকৃত হয়ে বাঁকানো বৃত্তচাপের মত হয়ে যায়। পাশে এবেল ১৬৮৯ স্তবকের আলোকচিত্রে এমন অনেকগুলো বৃত্তচাপ দেখা যাচ্ছে।[২০] এসব বৃত্তচাপ বিশ্লেষণ করে তমোপদার্থের যে বণ্টন ও ভর পাওয়া গেছে তা গতিবিদ্যা থেকে পাওয়া মানের সাথে বেশ সামঞ্জস্যপূর্ণ।[২১]
১৯৯০-এর দশক থেকে ছায়াপথ স্তবকের ভর বণ্টন পরিমাপের আরেকটি অত্যন্ত কার্যকরী উপায় ব্যবহৃত হয়ে আসছে। এর নাম দুর্বল মহাকর্ষীয় লেন্সিং। একটি নির্দিষ্ট স্তবকের কারণে পটভূমির কোন বস্তু থেকে আসা আলোর বিকৃতি পর্যবেক্ষণের পরিবর্তে এক্ষেত্রে অসংখ্য ছায়াপথ এবং স্তবকের জরিপ চালানো হয়। আসলে যেকোন বস্তুর কারণেই আলো বেঁকে যায়। কিন্তু বস্তুর ভর অনেক বেশি না হলে আমাদের পক্ষে দুরবিন দিয়ে স্পষ্টভাবে সেই বক্রতা পর্যবেক্ষণ করা সম্ভব হয় না। মহাবিশ্বের অধিকাংশ লেন্সিং ই আসলে আপাতদৃষ্টিতে শনাক্তকরণের অযোগ্য। এসব সূক্ষ্ণ সূক্ষ্ণ লেন্সিং ঘটনা বোঝার জন্য পটভূমির অসংখ্য ছায়াপথের ক্ষুদ্রাতিক্ষুদ্র বিকৃতি পারিসাংখ্যিক পদ্ধতিতে নির্ণয় করা হয়। এভাবে পুরোভূমির তমোপদার্থের ভর বণ্টন নির্ণয় করা গেছে যা একইসাথে সবল মহাকর্ষীয় লেন্সিং ও গতিবিদ্যার ফলাফলের সাথে সঙ্গতিপূর্ণ।[২২]

তবে এযাবৎ তমোপদার্থের উপস্থিতির সবচেয়ে সরাসরি প্রমাণ পাওয়া গেছে বুলেট স্তবক থেকে। সাধারণত দৃশ্যমান ও তমোপদার্থ তাদের পারস্পরিক মহাকর্ষের কারণে সর্বত্রই একসাথে থাকে। কিন্তু বুলেট নামক ছায়াপথ স্তবকটিতে ব্যতিক্রম এক চিত্র দেখা গেছে। বুলেট স্তবক মূলত দুটি ছায়াপথ স্তবকের সংঘর্ষরত অবস্থা। সংঘর্ষের কারণে এই স্তবকযুগলের তমোপদার্থ ও দৃশ্যমান পদার্থ আলাদা হয়ে গেছে। বুলেট থেকে আসা এক্স-রশ্মি বিশ্লেষণ করে দেখা গেছে এর সব গ্যাস কেন্দ্রের কাছাকাছি অবস্থিত। দুটি স্তবক একে অপরের ভেতর দিয়ে অতিক্রম করা সময় দুটির গ্যাস পরস্পরের আকর্ষণে ধীর হতে হতে কেন্দ্রের কাছাকাছি থিতু হয়েছে। মনে রাখতে হবে এসব গ্যাসীয় কণা মহাকর্ষের পাশাপাশি তড়িচ্চুম্বকীয় বলের মাধ্যমেও একে অপরের সাথে ক্রিয়া করে। কিন্তু তমোপদার্থের তেমন সংঘর্ষ বা মিথস্ক্রিয়ার ক্ষমতা নেই, সে মহাকর্ষ ছাড়া অন্য কোন বলের মাধ্যমেই ক্রিয়া করে না। এজন্য এক স্তবকের তমোপদার্থ অন্য স্তবকের তমোপদার্থকে পাশ কাটিয়ে পরস্পর থেকে এবং গ্যাস থেকেও দূরে সরে গেছে। এক্স-রশ্মিতে ৭-৮ কিলো ইলেকট্রন ভোল্টের এসব গ্যাস দেখা যাচ্ছে। কিন্তু একই স্তবকের দুর্বল মহাকর্ষীয় লেন্সিং করার পর দেখা যায় স্তবকের মোট ভরের একটি বিশাল অংশ কেন্দ্রীয় গ্যাস থেকে বেশ দূরে অন্য একটি স্থানে অবস্থান করছে। অর্থাৎ এমন স্থানে অধিকাংশ ভর পাওয়া যাচ্ছে যেখানে কোন আলো বা দৃশ্যমান বস্তু নেই। তমোপদার্থের এই পর্যবেক্ষণে নিউটন-আইনস্টাইনীয় মহাকর্ষের কোন আশ্রয়ই নেয়া হয়নি, এটি তাই ছায়াপথের ঘূর্ণন বক্রের অনিশ্চয়তা থেকে মুক্ত। এজন্যই অনেক বিজ্ঞানী এই পর্যবেক্ষণকে তমোপদার্থের সবচেয়ে সরাসরি প্রমাণ হিসেবে আখ্যায়িত করেন।[২৩]
এবেল ৫২০ বা ট্রেন-রেক স্তবক নামে পরিচিত আরেকটি সংঘর্ষরত স্তবকসমষ্টির ক্ষেত্রে একটু ভিন্ন ফলাফল পাওয়া গেছে। ট্রেন-রেক ছায়াপথের তিনটি ভিন্ন ভিন্ন স্থানে তমোপদার্থের আধিক্য দেখা গেছে যার একটি স্থান কেন্দ্রের কাছাকাছি। কেন্দ্রের এই স্থানটিতে প্রচুর তমোপদার্থ থাকার সম্ভাবনা থাকলেও নেই কোন দৃশ্যমান ছায়াপথ। বুলেট স্তবকের মত এখানেও দৃশ্যমান ও তমোপদার্থের ছাড়াছাড়ি ঘটেছে তবে সেটা অতো সরল নয়। এজন্য অনেকে তমোপদার্থের কণাগুলো নিজেদের মধ্যে কোন এক অজানা প্রক্রিয়ায় মিথস্ক্রিয়া করে বলতে চাইছেন।[২৪] এই অন্তঃমিথস্ক্রিয়ার মাত্রা কতটুকু হতে পারে তা নিয়ে গবেষণা চলছে। এক্ষেত্রে মূল প্রশ্নটি হচ্ছে, তমোপদার্থের চাপ আছে কিনা এবং থাকলে তাকে একটি আদর্শ তরল হিসেবে বিবেচনা করা যায় কিনা। তবে স্পষ্টতই ট্রেন-রেক স্তবক এই অন্তঃমিথস্ক্রিয়ার পক্ষে কথা বললেও বুলেট স্তবক বেশ জোরালোভাবেই বিপক্ষে কথা বলে। এরা একসাথে তাই তমোপদার্থের মডেলগুলোকেই প্রশ্নবিদ্ধ করে তোলে।[২৫]
বৃহৎ স্কেলের প্রবাহ
মহাবিশ্ব তথা স্থানকাল ক্রমাগত প্রসারিত হচ্ছে। সে হিসেবে প্রতিটি ছায়াপথেরই একে অপরের থেকে দূরে সরে যাওয়ার কথা। কিন্তু এর ব্যতিক্র দেখা যায়। যেমন, আকাশগঙ্গা ও অ্যান্ড্রোমিডা ছায়াপথ পরস্পরের দিকে অগ্রসরমান। মোটকথা মহাবিশ্বের বিভিন্ন বৃহৎ স্কেলের কাঠামোর এক ধরনের সার্বিক প্রবাহ বা গতি আছে। যেমন, আমাদের ছায়াপথ একটি স্থানীয় পুঞ্জের সদস্য যা মহাজাগতিক অণুতরঙ্গ পটভূমি বিকিরণের সাপেক্ষে প্রতি সেকেন্ডে প্রায় ৬২৭ কিলোমিটার বেগে প্রবাহিত হচ্ছে। এ ধরনের প্রবাহ বা গতির কারণ হিসেবে মহা বিস্ফোরণের পর দীর্ঘ দেগ হাজার কোটি বছরে মহাকর্ষের প্রভাবকে দায়ী করা হচ্ছে।
মহা বিস্ফোরণের ঠিক পরপর আমাদের মহাবিশ্ব সমসত্ত্ব ছিল না যার প্রমাণ সেই পটভূমি বিকিরণ থেকেই পাওয়া গেছে। পটভূমি বিকিরণে দৃশ্যমান অতি ক্ষুদ্র ক্ষুদ্র ঘনত্ব ব্যত্যয়গুলোই পরবর্তীকালে প্রসারণের বিরুদ্ধে বিভিন্ন পদার্থকে জমাট বেঁধে ছায়াপথ, ছায়াপথ স্তবক, তারা ইত্যাদি গঠন করতে সাহায্য করেছে। এসব অসমসত্ত্ব গঠনই মহাকর্ষের প্রভাবের মাধ্যমে বৃহৎ স্কেলের প্রবাহ সৃষ্টি করেছে। মহাবিশ্বের বৃহৎ স্কেলের কাঠামোগুলোর গতিবেগের ভেক্টর, ছায়াপথসমূহের বণ্টন ইত্যাদি পর্যবেক্ষণ করে মহাবিশ্বের ঘনত্ব রাশির এমন একটি মান নির্ণয় করা সম্ভব যা বৃহৎ স্কেলের প্রবাহকে ব্যাখ্যা করতে পারে। হিসাব করে দেখা গেছে,হলেই কেবল বৃহৎ স্কেলের এমন প্রবাহ থাকতে পারে। আর বলাই বাহুল্য যে পদার্থের ঘনত্ব রাশির এমন মানের জন্য প্রচুর তমোপদার্থ থাকতে হবে।[১৪]
তমোপদার্থের বণ্টন
সর্পিলাকার ছায়াপথে তমোপদার্থের বণ্টন সম্পর্কে সবচেয়ে বেশি জানা গেছে। এটি যে ছায়াপথের চাকতির অন্তর্ভুক্ত নয় তার পক্ষে বেশ কয়েকটি যুক্তি আছে। প্রথমত, আমাদের ছায়াপথ তথা আকাশগঙ্গাও একটি সর্পিলাকার ছায়াপথ। আকাশগঙ্গার তারাসমূহের উল্লম্ব বণ্টন এবং বিচ্ছুরণ বেগ বিশ্লেষণ করে দেখা গেছে এর চাকতিতে খুব বেশি তমোপদার্থ নেই। দ্বিতীয়ত, তমোপদার্থই মহাকর্ষ বলের দিক দিয়ে সবচেয়ে প্রভাবশালী বস্তু। কিন্তু মহাকর্ষের পুরো ভার একটি সরু চাকতিতে থাকতে পারে না। অন্য কথায় সরু self-gravitating চাকতি অস্থিতিশীল। তৃতীয়ত, হাইড্রোজেন চাকতির উপরে ও নিচে বেশ খানিকটা বিস্তৃত। কিন্তু তমোপদার্থ চাকতিতে থাকলে তার পক্ষে এত বিস্তৃত থাকা সম্ভব হতো না। এই বিস্তৃতিকে অনেক সময় hydrogen flaring বলা হয়।
সুতরাং সর্পিলাকার ছায়াপথের একটি সার্বিক চিত্র দাঁড় করানো যেতে পারে, দৃশ্যমান এবং তমোপদার্থকে মিলিয়ে। বর্তমান গবেষণা অনুযায়ী অপেক্ষাকৃত অনেক ক্ষুত্র বাল্জ ও চাকতি একটি বিশাল বড় তমোপদার্থের হেলোর মধ্যে প্রোথিত আছে। এই হেলোকে গোলকাকার হতে হবে এমন কোন কথা নেই। এটি কমলালেবুর মত উপর নিচে চ্যাপ্টা বা এমনকি triaxial ও হতে পারে। ভিরিয়াল উপপাদ্য ব্যবহার করে জানা গেছে দৃশ্যমান ছায়াপথের তুলনায় তমোপদার্থের হেলোর ব্যাসার্ধ্য ৫০ থেকে ১০০ গুণ বেশি এবং ভর প্রায় ১০ থেকে ২০ গুণ বেশি। এ কারণে বর্তমানে তমোপদার্থে বিশ্বাসীরা মনে করেন, প্রাচীন মহাবিশ্বে প্রথমে তমোপদার্থের “আভা” গঠিত হয়েছিল এবং পরে সেই “আভা”র মধ্যে দৃশ্যমান পদার্থ জড়ো হয়েছে।
বিকল্প ব্যাখ্যা
তমোপদার্থ দিয়ে ছায়াপথ এবং ছায়াপথ স্তবকের বিভিন্ন পর্যবেক্ষণের অসামঞ্জস্যতাকে ব্যাখ্যা করাটা বর্তমানে খুব জনপ্রিয় হলেও তমোপদার্থের প্রকৃতি সম্পর্কে কিছু জানা যায়নি এবং এই পদার্থ সরাসরি পর্যবেক্ষণ বা শনাক্ত করার সকল প্রচেষ্টাই এ পর্যন্ত ব্যর্থ হয়েছে। এ কারণে পর্যবেক্ষণের অসামঞ্জস্যতাগুলো ব্যাখ্যার জন্য কিছু বিকল্প অনুকল্প প্রস্তাব করা হয়েছে। বিকল্প অনুকল্পগুলোকে দুটি বড় শ্রেণীতে ভাগ করা যায়: সংশোধিত মহাকর্ষ সূত্র এবং কোয়ান্টাম মহাকর্ষ সূত্র। এই দুই ধরনের অনুকল্পের মধ্যে পার্থক্য হচ্ছে, সংশোধিত মহাকর্ষ সূত্রগুলো কেবল জ্যোতির্বৈজ্ঞানিক বা বিশ্বতাত্ত্বিক স্কেলে মহাকর্ষ বলের ভিন্ন ধরনের আচরণের কথা বলে কিন্তু কোয়ান্টাম স্কেল সম্পর্কে কিছু বলে না। তবে শেষ পর্যন্ত দুটো অনুকল্পই আলাদা আলাদা স্কেলে আইজাক নিউটন ও আলবার্ট আইনস্টাইনের প্রতিষ্ঠিত মহাকর্ষ সূত্রের সীমাবদ্ধতার কথা বলে।
সংশোধিত মহাকর্ষ তত্ত্ব
এ ধরনের সূত্র বলে, মহাবিশ্বের একটি বিশাল অংশ গুপ্ত নেই বরং যে মহাকর্ষ সূত্র ব্যবহারের কারণে এমন পদার্থের প্রয়োজন পড়ছে সেই সূত্রকেই কিছু বিশেষ ক্ষেত্রে সংশোধন করতে হবে। এ ধরনের প্রথম অনুকল্প দিয়েছিলেন ইসরাইলী বিজ্ঞানী মর্ডেহাই মিলগ্রম, ১৯৮৩ সালে। তার অনুকল্পের নাম সংশোধিত নিউটনীয় গতিবিদ্যা, ইংরেজিতে Modified Newtonian Dynamics আর সংক্ষেপে MOND বা মন্ড। এই অনুকল্প বলে, মহাকর্ষীয় ত্বরণের মান যখন অনেক কমে যায় তখন নিউটনের সূত্রকে এমনভাবে সংশোধন করতে হবে যাতে অপেক্ষাকৃত শক্তিশালী মহাকর্ষীয় ক্ষেত্র সৃষ্টি হয়। নিউটনের সূত্র অনুসারে একটি বস্তু থেকে আরেকটি বস্তুর দূরত্ব যত বাড়বে মহাকর্ষীয় বল তত কমতে থাকবে। সূতরাং ছায়াপথের কেন্দ্র থেকে তারার দূরত্ব যত বেশি তার উপর মহাকর্ষীয় বল তত কম এবং তথাপি তারাটির ঘূর্ণন বেগ তত কম হওয়ার কথা। ভেরা রুবিন ও অন্যদের পর্যবেক্ষণে দেখা গিয়েছিল বেগ কমছে না বরং অনেক দূর পর্যন্ত ধ্রুব থাকছে। তাই মন্ড বলল, অনেক দূরে গেলে মহাকর্ষীয় ক্ষেত্র যতোটা দুর্বল হয়ে যায় বলে ভাবা হয়েছিল ততোটা হয় না।[৭]
উপবৃত্তীয় এবং বামন উপবৃত্তীয় ছায়াপথের ঘূর্ণন লেখ ব্যাখ্যায় মন্ড সফল হয়েছে। কিন্তু ছায়াপথ স্তবকের মহাকর্ষীয় লেন্সিং ব্যাখ্যায় এটি সফল হয়নি। উপরন্তু মন্ড কোন আপেক্ষিকতাভিত্তিক তত্ত্ব নয়। কারণ কেবল নিউটনের মহাকর্ষ সূত্রকে সংশোধনের মাধ্যমে এর জন্ম হয়েছিল কিন্তু মহাকর্ষের সর্বাধুনিক তত্ত্ব সাধারণ আপেক্ষিকতার সাথে এর সম্পর্ক ছিল না। ১৯৮৩ সালের পরপরই মন্ডকে আপেক্ষিকতার সাথে মেলানোর প্রচেষ্টা শুরু হয়। এখনও চেষ্টা চলছে এবং বেশ কয়েকটি গাণিতিক অনুকল্প উঠে এসেছে। যেমন, টেভেস, স্কেলার-টেন্সর-ভেক্টর মহাকর্ষ, ফেনোমেনোলজিক্যাল কোভ্যারিয়েন্ট প্রচেষ্টা ইত্যাদি।[২৭]
২০০৭ সালে কানাডীয় পদার্থবিজ্ঞানী জন মফেট অপ্রতিসম মহাকর্ষ তত্ত্বের উপর ভিত্তি করে একটি সংশোধিত মহাকর্ষ সূত্র দিয়েছেন যার সংঘর্ষরত ছায়াপথের আচরণ ব্যাখ্যা করতে পারার কথা।[২৮] এটি সত্য হতে হলে অনাপেক্ষিক নিউট্রিনো বা অন্যান্য শীতল তমোপদার্থের অস্তিত্ব থাকতে হবে।
আরেকটি প্রস্তাবে বলা হয়েছে, হয়ত মহাকর্ষ একটি ক্রিয়া-প্রতিক্রিয়ার ব্যবস্থা বা অবিরাম ফিডব্যাক বা পুনর্নিবেশের মাধ্যমে কাজ করে। অর্থাৎ একটি বস্তু প্রথমে অন্যটির উপর ক্রিয়া করে, তারপর অন্যটি প্রতিক্রিয়া দেখায় এবং এরপর প্রথম বস্তুটি পুনঃপ্রতিক্রিয়া জানায়। মোটকথা, ক বস্তু খ বস্তুকে প্রভাবান্বিত করে, খ আবার ক এর উপর প্রভাব ফেলে, এরপর ক আবার খ এর উপর এবং এভাবে চলতেই থাকে। এই পুনর্নিবেশ প্রক্রিয়ায় মহাকর্ষ বলের শক্তি বৃদ্ধি পায়।[২৯]
সম্প্রতি আরেকটি দল তমোতরল বা ডার্ক ফ্লুয়িড নামক আরেকটি অনুকল্প প্রস্তাব করেছে যা বৃহৎ-স্কেলে মহাকর্ষ সূত্র সংশোধনের কথা বলে। এই অনুকল্প বলে আকর্ষণধর্মী অতিরিক্ত যে মহাকর্ষীয় শক্তিটি তমোপদার্থের কারণে উদ্ভূত হয় বলা হচ্ছে তা আসলে তমোশক্তির একটি পার্শ্ব-প্রতিক্রিয়া। এটি অনুসারে তমোপদার্থ ও তমোশক্তি একসাথে একটি শক্তির ক্ষেত্র গঠন করে যা বিভিন্ন স্কেলে বিভিন্ন ধরনের প্রতিক্রিয়া দেখায়। এটি আসলে পূর্ববর্তী একটি তরল-অনুকল্পের অপেক্ষাকৃত সহজ সংস্করণ। সাধারণীকৃত চ্যাপলুগিন গ্যাস নামে পরিচিত সেই তরল-অনুকল্পে বলা হয়েছিল সমগ্র স্থানকালই এক ধরনের সংনম্য গ্যাস। তমোতরলকে বায়ুমণ্ডলের সাথে তুলনা করা যেতে পারে। বায়ুমণ্ডল প্রসারণশীল কিন্তু স্থানে স্থানে সেই বায়ু জমাট বেঁধে মেঘ তৈরি করতে পারে। তেমনিভাবে তমোতরল প্রসারণশীল কিন্তু ক্ষেত্রবিশেষে বিভিন্ন ছায়াপথের চারদিকে জড়ো হয়ে সে ছায়াপথের পদার্থগুলোকে আবদ্ধ রাখতে সাহায্য করতে পারে।[৩০]
আরেকটি সম্ভাব্যতা হচ্ছে স্থানকালের জন্য দুটি মেট্রিক টেন্সর ব্যবহার। গাণিতিকভাবে দেখা গেছে সময়কে বিপরীত করে দিয়ে সাধারণ আপেক্ষিকতার গ্রহণযোগ্য সমাধান পেতে হলে এমন দ্বৈত মেট্রিক টেন্সরের প্রয়োজন পড়ে।[৩১] তমোপদার্থ ও তমোশক্তি দুটোকেই সাধারণ আপেক্ষিকতার সময় বিপরীত করে দেয়া সমাধান হিসেবে ব্যাখ্যা করা যায়।[৩২]
কোয়ান্টাম মহাকর্ষ
কোয়ান্টাম মহাকর্ষ আধুনিক পদার্থবিজ্ঞানের খুব সক্রিয় একটি গবেষণা ক্ষেত্র। এর অধীনে একাধিক তত্ত্ব আছে যার একটি আবার অন্যটির সাথে প্রতিযোগিতায় মত্ত। অনেক সময় একে সবকিছুর তত্ত্ব বা থিওরি অফ এভরিথিং বলা হয়। মূলত এটি হচ্ছে বেশ কিছু তত্ত্বের একটি সাধারণ শ্রেণী যা পদার্থবিজ্ঞানের দুটি বৃহৎ ক্ষেত্রকে একত্রিত করার চেষ্টা করে। ক্ষেত্র দুটি হচ্ছে মহাকর্ষ এবং কোয়ান্টাম বলবিদ্যা। কোয়ান্টাম মহাকর্ষ তত্ত্বের উদাহরণ হিসেবে সুপারস্ট্রিং তত্ত্ব, এর উত্তরসূরী এম-তত্ত্ব এবং এদের প্রতিযোগী লুপ কোয়ান্টাম মহাকর্ষ তত্ত্বের নাম করা যায়।
অনেকেই মনে করেন, তমোপদার্থ গবেষণার চেয়ে কোয়ান্টাম মহাকর্ষ নিয়ে কাজ করাটা অনেক মৌলিক এবং আকর্ষণীয় একটি বিষয়। কারণ কোয়ান্টাম মহাকর্ষ প্রকৃতির সকল মৌলিক বলকে একটি সূত্রের মাধ্যমে ব্যাখ্যার চেষ্টা চালিয়ে যাচ্ছে। এই অতি মৌলিক তত্ত্বটি প্রতিষ্ঠিত হয়ে গেলে তা দিয়ে তমোপদার্থের মত সকল সমস্যার সমাধান করা যাবে বলে মনে করেন অনেকে। কারণ তমোপদার্থ একটি চিরায়ত সমস্যা সমাধানের জন্য প্রস্তাবকৃত একটি চিরায়ত পদার্থবিজ্ঞানের সমাধান।
সুপারস্ট্রিং বা এম-তত্ত্ব গবেষকরা বলেন, আমাদের দৃশ্যমান মহাবিশ্বের বাইরে অবস্থিত বহুমাত্রিক জগৎ আমাদের জগৎকে প্রভাবিত করে। তাই মহাকর্ষ বলে অসামঞ্জস্য ব্যাখ্যার জন্য আর তমোপদার্থের প্রয়োজন পড়বে না, বিশ্বতত্ত্বের একীভূত তত্ত্ব দিয়েই তা করা যাবে। এম-তত্ত্ব বলে আমাদের অতি পরিচিত স্থানের তিনটি মাত্রা ও কালের একটি মাত্রাই শেষ কথা নয়, মহাবিশ্বে মোট ১১টি মাত্রা রয়েছে। বাকি ৭টি মাত্রা আমাদের থেকে লুকিয়ে আছে এবং কেবল কোয়ান্টাম স্কেলেই তারা প্রভাব রাখতে পারে। যদি এই অতিরিক্ত মাত্রাগুলোতে কণা বা শক্তি থাকে তাহলে সেগুলোই হয়ে উঠতে পারে তমোপদার্থের বিকল্প।
লুপ কোয়ান্টাম মহাকর্ষ (বা এর উপসেট লুপ কোয়ান্টাম বিশ্বতত্ত্ব) বলে, মহাবিশ্ব তথা স্থানকাল নিজেই মৌলিক কণা বা কোয়ান্টা দিয়ে গঠিত। এটি আমাদের সাধারণ চিন্তার বিপরীতে যায়। আমরা মনে করি শূন্য স্থান একেবারেই শূন্য, কিন্তু লুপ কোয়ান্টাম তত্ত্বগুলো বলে শূন্যস্থানও কিছু একটা দিয়ে গঠিত। স্থানকালের প্রতিটি কণা অন্য প্রতিবেশী কণার সাথে মিলে এক ধরনের লুপ তৈরি করে যার মাধ্যমে সৃষ্টি হয় মহাবিশ্বের সকল পদার্থ ও শক্তির। শূন্যস্থানে কোন লুপ বা মোচড় বা ভাজ থাকে না, কিন্তু পদার্থ বা শক্তির নিকটে অবস্থিত লুপহীন শূন্যস্থান পদার্থ বা শক্তি থেকে অনেক দূরে অবস্থিত লুপহীন শূন্যস্থানের তুলনায় বেশি টান অনুভব করে। একটি সুদীর্ঘ শিকল কল্পনা করা যাক যার মাঝখানটাতে গুঁট দেয়া আছে। গিঁটের কাছাকাছি থাকা শিকলের অংশটুকু দূরের চেয়ে বেশি টান অনুভব করবে, এটা হতে পারে তমোপদার্থের ব্যাখ্যা। আর গিঁট থেকে অনেক দূরে থাকা শিকলের অংশটুকু তেমন কোন টান অনুভব করবে না, বেশ শিথিল থাকবে, এটা হতে পারে তমোশক্তির ব্যাখ্যা।
২০০৪ সালে জার্মানির ইউনিভার্সিটি অফ মাইনৎস থেকে প্রকাশিত একটি গবেষণায় বলা হয়েছে, কেউ যদি নিউটনের মহাকর্ষীয় ধ্রুবকের উপর বিভিন্ন স্কেলে একেবারে সাধারণ কোয়ান্টাম বলবিদ্যা প্রয়োগ করে তাহলে দেখা যায়, মহাকর্ষীয় ধ্রুবকটি আর অতোটা ধ্রুব থাকে না। অর্থাৎ সৌর জগৎ থেকে শুরু করে ছায়াপথ পর্যন্ত একেক স্কেলে ধ্রুবকটির মান একেক রকম, আসলে স্কেল যত বাড়ে ধ্রুবকের মানও তত বাড়ে। এটি সত্যি হলে দূরের তারাগুলো কেন বেশি বল অনুভব করে তা বোঝা যাবে। সেক্ষেত্রে তমোপদার্থের আর কোন প্রয়োজন পড়বে না।[৩৩]
তথ্যসূত্র
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.












