২-এর বর্গমূল

গণিতে ২ এর বর্গমূল, লিখিত ${\displaystyle {\sqrt {2}}}$ ও ${\displaystyle 2^{1/2}}$, হলো একটি ধণাত্মক অমূলদ সংখ্যা যাকে নিজের সাথে গুণ করার ফলাফল ২। যেহেতু ${\displaystyle -{\sqrt {2}}}$ কে নিজের সাথে গুণ করলেও একই ফলাফল পাওয়া যায়, সেহেতু ${\displaystyle {\sqrt {2}}}$ থেকে এর ঋণাত্মক প্রতিপক্ষ আলাদা করতে একে অধিক সঠিকভাবে দুই এর প্রধাণ বর্গমূল বলা যায়। ^[1]
জ্যামিতির ভাষায়, পিথাগোরাসের উপপাদ্য অনুসারে ২ এর বর্গমূল হল এক একক দৈর্ঘ্য সম্পন্ন বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য। ${\displaystyle {\sqrt {2}}}$ সংখ্যাটিকে সর্বপ্রথম আবিষ্কৃত অমূলদ সংখ্যা হিসেবে ধরা হয়। ^[2]

ডেডেকাইন্ড দুটি ধনাত্মক যুক্তিযুক্ত সংখ্যা ব্যবহার করে একটি অযৌক্তিক সংখ্যা √২ নির্ধারণ করে কাটা

২ এর বর্গমূলের মূলদ সন্নিকট,${\displaystyle \left[{\frac {665857}{470832}}\right]}$,যাহা ,পাওয়া যায় ব্যাবিলনীয় অ্যালগরিদমের চতুর্থ ধাপ থেকে, যা শুরু হয় a_০=১ থেকে এবং ইহা আপাতভাবে খুব বড় ১.৬×১০^−১২ : ইহার বর্গ হল ২.০০০০০০০০০০৪৫...
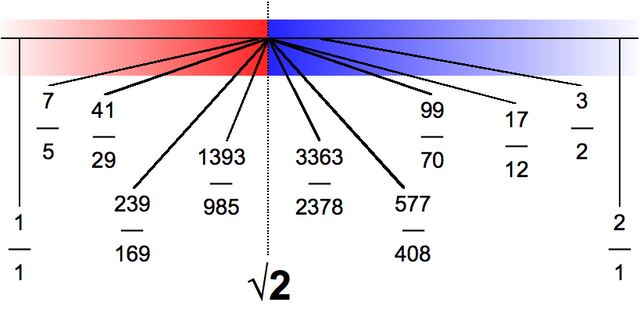
সাধারণত মূলদ সন্নিকট ${\displaystyle {\frac {99}{70}}}$(≈১.৪১৪২৯) ব্যবহৃত হয়. ইহার হর ৭০, তা ছাড়াও ইহা সঠিক মানের চেয়ে ${\displaystyle {\frac {1}{10,000}}}$(প্রায় +০.৭৪×১০^−৪) কম. যেহেতু ইহা ২ এর বর্গমূলের অবিরত ভগ্নাংশের খুব নিকটে তাই যে কোন মূলদ সন্নিকট যাহার হর ১৬৯ এর থেকে ছোট তাকে উন্নততর বলা যেতে পারে যেহেতু ${\displaystyle {\frac {239}{169}}}$এর পরবর্তী সন্নিকটের ত্রূটি প্রায় -০.১২×১০^−৪.
${\displaystyle {\sqrt {2}}}$ এর সাংখিক মান (সংক্ষিপ্ত) দশমিকের পর ৬৫ ঘর পর্যন্তপর্যন্ত হল:
১.৪১৪২১ ৩৫৬২৩ ৭৩০৯৫ ০৪৮৮০ ১৬৮৮৭ ২৪২০৯ ৬৯৮০৭ ৮৫৬৯৬ ৭১৮৭৫ ৩৭৬৯৪ ৮০৭৩১ ৭৬৬৭৯ ৭৩৭৯৯...(ওইআইস (OEIS) এর অনুক্রম A০০২১৯৩ অনুযায়ী)

ইতিহাস

ব্যাবিলনের একটি মাটির বাড়ি YBC ৭২৮৯(১৮০০-১৬০০ খ্রীষ্ট্পূর্বাব্দে) তে চারটি ষড়ভূজাকৃতি গঠন ১ ২৪ ৫১ ১০ লক্ষ্য করা গেছে যাহা ${\displaystyle {\sqrt {2}}}$ এর সঠিক নিকটস্থ মান উল্লেখ করে^[১] যেহেতু ইহাতেও ছয় দশমিক অঙ্ক উপস্থিত রয়েছে এবং ইহাই ${\displaystyle {\sqrt {2}}}$ এর সবচেয়ে সঠিক তিন ঘর ষড়ভূজাকৃতি উপস্থাপনা, যা হল:

1${\displaystyle +{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}}$=${\displaystyle {\frac {30547}{21600}}}$=${\displaystyle 1.41421296...}$

তথ্যসূত্র

1. Weisstein, Eric W.। "Principal Square Root"। mathworld.wolfram.com (ইংরেজি ভাষায়)। সংগ্রহের তারিখ ২০২৩-০৭-১৩।
2. "Oldest irrational numbers - Guinness World Records"। Guinness World Records।