লগারিদম

গণিতশাস্ত্রে লগারিদম হলো সূচকের বিপরীত প্রক্রিয়া। এর অর্থ কোনো সংখ্যার লগারিদম হলো সেই সূচক যেটাকে একটি নির্ধারিত মানের (ভিত্তি) ঘাত হিসাবে উন্নীত করলে প্রথমোক্ত সংখ্যাটি পাওয়া যায়। সহজভাবে, একটি সংখ্যাকে বার বার গুণ করলে, লগারিদম সংখ্যাটিকে যতবার গুণ করা হয়েছিল তা গণনা করে। যেমন: যেহেতু 1000 = 10 × 10 × 10 = 10³ তাই 1000 এর দশ ভিত্তিক লগারিদম হলো 3, অথবা log₁₀ (1000) = 3। x এর b ভিত্তিক লগারিদম কে লেখা হয় log_bx

২ভিত্তিক লগারিদমের লেখচিত্র x অক্ষের (আনুভূমিক অক্ষ) ১ বিন্দুতে ছেদ করে এবং (২, ১), (৪, ২), এবং (৮, ৩) বিন্দু দিয়ে অতিক্রম করে।. উদাহরণস্বরূপ, log₂(8) = 3, কারণ 2³ = 8. রেখাটি ক্রমশ y অক্ষের নিকটবর্তী হতে থাকে কিন্তু কখনও yঅক্ষের সাথে মিলিত হয় না বা ছেদ করে না।.

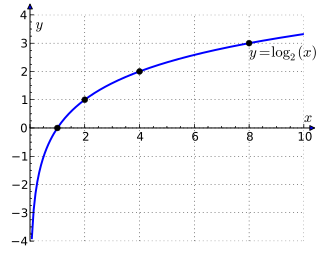
10 ভিত্তিবিশিষ্ট লগকে (অর্থাৎ b=10) সাধারণ লগারিদম বলা হয় এবং এটিকে বিজ্ঞানী ও প্রকৌশলীরা সাধারণত ব্যবহার করে থাকে। স্বাভাবিক লগারিদমে ভিত্তি হিসেবে গাণিতিক ধ্রুবক e(অর্থাৎ b≈2.718) কে ব্যবহার করা হয়। গণিতবিদ ও পদার্থবিদ গণ স্বাভাবিক লগারিদম ব্যবহার করে থাকে। বাইনারি লগে 2 কে ভিত্তি হিসেবে ব্যবহার করা হয় এবং কম্পিউটার বিজ্ঞানে ব্যবহৃত হয়।

১৬১৪ সালে সর্বপ্রথম জন নেপিয়ার লগারিদম এর ধারণা দেন। লগারিদম টেবিল ব্যবহার করে সহজেই দুইটি সংখ্যার গুণ করা যায়। কারণ ${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y,}$

নামের উৎপত্তি

Logos এবং Arithmas নামক দুটি গ্রিক শব্দ হতে Logarithm শব্দটির উৎপত্তি। Logos অর্থ "আলোচনা" এবং Arithmas অর্থ "সংখ্যা"। অর্থাৎ, Logarithm শব্দটির অর্থ "সংখ্যা বিষয়ক আলোচনা" বা "সংখ্যা-সম্পর্কিত আলোচনা"।^[১]

আলোচনার বিষয়

একটি পূর্ণাঙ্গ 3-ary ট্রি ব্যবহার করে 3 এর সূচকগুলো প্রত্যক্ষ করা যায় এবং লগারিদমের সাথে সেগুলো কীভাবে সম্পর্কিত তা বোঝা যায়।

সাধারণ ক্ষেত্রে লগারিদম একটি সংখ্যা (ভিত্তি) কতবার গুণ করা হলো সেটা গণনা করে। উদাহরণস্বরূপ, ১০০০ এর ১০ ভিত্তিক লগের মান ৩, এর অর্থ হলো ১০ এর ঘাত ৩ এ উন্নীত করলে ১০০০ পাওয়া যায় (১০০০ = ১০ × ১০ × ১০ = ১০^৩)। এখানে ১০ সংখ্যাটি ৩ বার গুণ করলে ১০০০ পাওয়া যায়। আরও সাধারণভাবে বলা যায়, কোনো ধনাত্মক প্রকৃত সংখ্যাকে যেকোনো প্রকৃত ঘাতে উন্নীত করলে সবসময় ধনাত্মক ফল পাওয়া যায়, সুতরাং যে কোনো দুটি ধনাত্মক প্রকৃত সংখ্যা b এবং x এর লগারিদম নির্ণয় করা যায় যেখানে b সংখ্যাটি ১ এর সমান নয়। x এর b ভিত্তিক লগকে প্রকাশ কর হয় এভাবে log_b(x), এবং এর মান একটি অনন্য প্রকৃত সংখ্যা y এমন যে,

b^y = x.

উদাহরণস্বরূপ, যেহেতু ৬৪ = ২^৬, তাহলে আমরা পাই

log_২(৬৪) = ৬

১০ ভিত্তিক লগারিদমকে (অর্থাৎ b = ১০) বলা হয় সাধারণ লগারিদম, বিজ্ঞান ও প্রকৌশল বিদ্যায় এর বহুবিধ ব্যবহার রয়েছে। স্বাভাবিক লগারিদম এর ভিত্তি হলো একটি গাণিতিক ধ্রুবক E (≈ ২.৭১৮); সহজ ডেরিভেটিভ (derivative) এর কারণে গণিত ও পদার্থবিদ্যায় এর বিস্তৃত ব্যবহার রয়েছে। দ্বিমিক লগারিদম এ ভিত্তি হিসাবে ব্যবহৃত হয় ২ (অর্থাৎ b = ২) এবং এটা সাধারণভাবে কম্পিউটার বিজ্ঞান ব্যবহৃত হয়।

সাধারণ লগারিদম

মূল নিবন্ধ: সাধারণ লগারিদম

Canon logarithmorum

যেহেতু দশ এর সাধারণ লগারিদমের ফলাফল এক, একশ এর সাধারণ লগারিদমের ফলাফল দুই এবং একহাজার এর সাধারণ লগারিদমের ফলাফল তিন সেক্ষেত্রে সাধারণ লগারিদমের ধারণা অনেকটাই দশমিক-অবস্থানগত সংখ্যা পদ্ধতির কাছাকাছি । ধরা হয় সাধারণ লগ এর বেস ১০ টি , তবে পূর্ব এশিয়ায় এখনও বেস ১০,০০০ প্রচলিত যা বেশ পুরাতন । আর্কিমিডিস তার দ্য স্যান্ড রেকনার বইটিতে একটি পরিকল্পিত সংখ্যা পদ্ধতি স্বরূপ দশসহস্র বেস ব্যবহার করেন যা পৃথিবীতে উৎপাদিত শস্য গণনায় তাকে সহায়তা করে ।^[২]

প্রাচীনকালে আর্কিমিডিস সংখ্যায় জ্যামিতিক ধারা ব্যবহার করে এবং একটি গাণিতিক ধারার সাথে সম্পর্কিত করে গুণ হ্রাস করার জন্য একটি প্রণালী অনুসরণ করেন ।

১৬১৬ সালে হেনরি ব্রিগস নেপিয়ার লগারিদম এর প্রস্তাবিত পরিবর্তন এর জন্য নেপিয়ার এর সাথে এদিনবরাতে সাক্ষাত করেন। পরের বছর তিনি আবার একই উদ্দেশ্যে সেখানে যান। এই আলোচনার সময় তার প্রস্তাবিত পরিবর্তনটিতে নেপিয়ার রাজি হয়েছিল এবং ১৬১৭ সালে এডিনবার্গের দ্বিতীয় সফর থেকে ফিরে আসার পর তিনি তার লগারিদমগুলির প্রথম সহস্র প্রকাশ করেন।

১৬২৪ সালে ব্রিগস তার এরিথমেটিকা লগারিথমিকা প্রকাশ করেছিলেন, একটি কাগজে তিনি ত্রিশ হাজার স্বাভাবিক সংখ্যার ( ১-২০,০০০ এবং ৯০,০০০-১০০,০০০) চৌদ্দ দশমিক স্থান পর্যন্ত লগারিদম প্রকাশ করে। এই টেবিল পরবর্তীতে ১৯৫২ সালে Adriaan Vlacq দশ স্থান পর্যন্ত এবং আলেকজান্ডার জন থম্পসন বিশ স্থান পর্যন্ত বৃদ্ধি করেন।

ব্রিগস ছিলেন প্রথম বাক্তিদের একজন যিনি ফাংশন টেবিল গণনা সীমাবদ্ধ-পার্থক্য পদ্ধতি ব্যবহার করেন। তিনি প্রতিটি ডিগ্রির শতভাগ অংশে চৌদ্দ দশমিক স্থান পর্যন্ত প্রাকৃতিক সাইনের পনেরটি স্থান এবং দশটি স্থানে একইরকম টাঙ্গেন্ট এবং সেকেন্ডের সাথে লগারিদমিক সাইন এবং ট্যানজেন্টগুলির একটি টেবিলও সম্পন্ন করেন, যা গৌড়ায় ছাপা হয়। ১৬৩১ সালে এবং ট্রাইগোনোম্রিয়া ব্রিটানিকা শিরোনামের অধীনে ১৬৩৩ সালে এটি প্রকাশিত হয়; এই কাজ সম্ভবত তার ১৬১৭ "লগারিদমাম চিলিয়াস প্রিমা" ("প্রথম থাউসন্ড লগারিদমস") এর উত্তরাধিকারী, যা লগারিদমগুলির একটি সংক্ষিপ্ত হিসাব এবং ১৪ তম দশমিক স্থান থেকে গণনা করা প্রথম ১০০০ পূর্ণসংখ্যার একটি দীর্ঘতর টেবিল দেয়।

স্বাভাবিক লগারিদম

মূল নিবন্ধ: স্বাভাবিক লগারিদম

Opus geometricum posthumum, 1668

১৬৪২ সালে গ্রেগোয়োর ডি সেন্ট-ভিনসেন্টের প্রাক্তন ছাত্র আলফসন অ্যান্টোনিও দে সারাসা,^[৩] হাইপারবোলার চতুর্থাংশের সাথে সম্পর্কিত লগারিদমগুলি নির্দেশ করেছিলেন যে অধিবৃত্তের ক্ষেত্রফল A(t), x = 1 থেকে x=t পর্যন্ত সন্তুষ্ট ^[৪]

${\displaystyle A(tu)=A(t)+A(u).}$

স্বাভাবিক লগারিদম সর্বপ্রথম নিকোলাস মারকেটর দ্বারা ১৬৬৮ সালে তার কাজ লগারিথোমোটেকিয়া তে প্রকাশিত হয়েছিল,^[৫] যদিও গণিতের শিক্ষক জন স্পিডেল ১৬৯২ সালে নেপিয়রের কাজের উপর ভিত্তি করে কার্যকরভাবে প্রাকৃতিক লগারিদমগুলির একটি টেবিল সংকলন করেছিলেন। ^[৬]

ইতিহাস

মূল নিবন্ধ: লগারিদমের ইতিহাস

গণনা সহজ করার জন্য সপ্তদশ শতাব্দীর শুরুর দিকে জন নেপিয়ার লগারিদম এর সূচনা করেন।^[৭] স্লাইড রুল এবং লগ সারণি ব্যবহার করে সহজে গণনার জন্য নাবিক, বৈজ্ঞানিক, প্রকৌশলী এবং অন্যান্যরা খুব দ্রুতই এগুলো গ্রহণ করেন। বিরক্তিকর বহুসাংখ্যিক গুণনের ধাপসমূহ লগারিদমের নিয়মে একটি সরল যোগে পরিণত হয়। লগারিদমের নিয়মানুযায়ী সংখ্যাসমূহের গুণফলের লগারিদম এর মান সংখ্যাগুলোর একক লগারিদমের মানের যোগফল। অর্থাৎ

${\displaystyle \log _{b}(xy)=\log _{b}(x)+\log _{b}(y),\,}$

এখানে b, x and y সকলে ধনাত্মক এবং b ≠ 1. বর্তমানের লগারিদমের ধারণা এসেছে লেওনার্ড অয়লার নিকট থেকে, যিনি অষ্টাদশ শতাব্দীতে লগারিদমকে সূচক অপেক্ষকের সূচক ফাংশন সাথে সম্পর্কযুক্ত করেন। যেকোন জটিল সংখ্যাকে A.e^iø, A≥0, আকারে প্রকাশ করা যায়। এই ধারণা থেকেই ঋণাত্মক সংখ্যা ও জটিল সংখ্যার লগারিদম সংজ্ঞায়িত করা যায়। তাহলে z একটি জটিল সংখ্যা হলে যদি এর মডুলাস |z|, আর্গুমেন্ট ø হয় তবে ln(z)=ln|z| +iø, এখন একটি জটিল সংখ্যার অসংখ্য আর্গুমেন্ট থাকে। কাজেই বলা যায় কোন সংখ্যার লগারিদমের অসংখ্য মান থাকতে পারে। তবে তার মুখ্য মান কেবল একটি। যেমন, z যদি ধনাত্মক সংখ্যা হয়, তবে |z|=z, মুখ্য আর্গুমেন্ট ø=0, কাজেই এর স্বাভাবিক লগারিদমের মুখ্য মান ln(z)।

২০০০-১৬০০ খ্রিস্টপূর্বাব্দে বাবিলীয়রা দুটি সংখ্যা গুণের ফলাফলের জন্য শুধু যোগ ,বিয়োগ এবং চতুর্থাংশের চতুর্থাংশের একটি টেবিল ব্যবহার করে চতুর্থাংশ বর্গ গুণগত অ্যালগরিদম আবিষ্কার করতে পারে। সুতরাং, যেমন একটি টেবিল অনুরূপ উদ্দেশ্য লগারিদম টেবিলের পরিসেবা দেয়, যা সংযোজন এবং টেবিল সন্ধানগুলি ব্যবহার করে গণনাকে গণনা করার অনুমতি দেয়। যাইহোক, চতুর্থাংশ-বর্গক্ষেত্র পদ্ধতি পারস্পরিক পরিসরের অতিরিক্ত টেবিলের (অথবা পারস্পরিক উৎপাদনের জন্য পর্যাপ্ত সহজ অ্যালগরিদমের জ্ঞান) ছাড়াই ব্যবহার করতে পারে না। চতুর্থাংশ স্কোয়ারের বড় টেবিলগুলি কম্পিউটারের ব্যবহার দ্বারা ১৮৭২ সাল পর্যন্ত বৃহত্তর সংখ্যার সঠিক গুণমান সরল করার জন্য ব্যবহার করা হয়েছিল।

সূত্রাবলী

লগারিদম এর কয়েকটি গুরুত্বপূর্ণ সূত্র রয়েছে।

গুণ, ভাগ, ঘাত ও মূল

দুইটি সংখ্যার গুণফলের লগ সংখ্যা দুইটির লগ এর যোগফল। দুইটি সংখ্যার ভাগফলের লগ সংখ্যা দুইটির লগের বিয়োগ ফলের সমান। নিচে লগারিদম এর সূত্রাবলীর তালিকা দেওয়া হলো।

	সূত্র	উদাহরণ
গুণ	${\displaystyle \log _{b}(xy)=\log _{b}(x)+\log _{b}(y)}$	${\displaystyle \log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5}$
ভাগ	${\displaystyle \log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)}$	${\displaystyle \log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4}$
ঘাত	${\displaystyle \log _{b}(x^{p})=p\log _{b}(x)}$	${\displaystyle \log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6}$
মূল	${\displaystyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}}$	${\displaystyle \log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

তথ্যসূত্র

1. উচ্চতর গণিত, নবম-দশম শ্রেণি, জাতীয় শিক্ষাক্রম ও পাঠ্যপুস্তক বোর্ড, ঢাকা, বাংলাদেশ। শিক্ষাবর্ষ ২০২১।
2. Ian Bruce (2000) "Napier’s Logarithms", American Journal of Physics 68(2):148
3. In 1647, Gregoire de Saint-Vincent published his book, Opus geometricum quadraturae circuli et sectionum coni (Geometric work of squaring the circle and conic sections), vol. 2 (Antwerp, (Belgium): Johannes and Jakob Meursius, 1647). On page 586, Proposition CIX, he proves that if the abscissas of points are in geometric proportion, then the areas between a hyperbola and the abscissas are in arithmetic proportion. This finding allowed Saint-Vincent's former student, Alphonse Antonio de Sarasa, to prove that the area between a hyperbola and the abscissa of a point is proportional to the abscissa's logarithm, thus uniting the algebra of logarithms with the geometry of hyperbolas. See: Alphonse Antonio de Sarasa, Solutio problematis a R.P. Marino Mersenne Minimo propositi ... [Solution to a problem proposed by the reverend father Marin Mersenne, member of the Minim order ... ], (Antwerp, (Belgium): Johannes and Jakob Meursius, 1649). Sarasa's critical finding occurs on page 16 (near the bottom of the page), where he states: "Unde hae superficies supplere possunt locum logarithmorum datorum ... " (Whence these areas can fill the place of the given logarithms ... ). [In other words, the areas are proportional to the logarithms.] See also: Enrique A. González-Velasco, Journey through Mathematics: Creative Episodes in Its History (New York, New York: Springer, 2011), page 118.
4. Alphonse Antonio de Sarasa, Solutio problematis a R.P. Marino Mersenne Minimo propositi ... [Solution to a problem proposed by the reverend father Marin Mersenne, member of the Minim order ... ], (Antwerp, (Belgium): Johannes and Jakob Meursius, 1649).
   Sarasa realized that given a hyperbola and a pair of points along the abscissa which were related by a geometric progression, then if the abscissas of the points were multiplied together, the abscissa of their product had an area under the hyperbola which equaled the sum of the points' areas under the hyperbola. That is, the logarithm of an abscissa was proportional to the area, under a hyperbola, corresponding to that abscissa. This finding united the algebra of logarithms with the geometry of hyperbolic curves.

   • Sarasa's critical finding occurs on page 16 (near the bottom of the page), where he states: "Unde hae superficies supplere possunt locum logarithmorum datorum ... " (Whence these areas can fill the place of the given logarithms ... ). [In other words, the areas are proportional to the logarithms.]
   • See also: Enrique A. González-Velasco, Journey through Mathematics: Creative Episodes in Its History (New York, New York: Springer, 2011), pp. 119–120.
5. J. J. O'Connor; E. F. Robertson (সেপ্টেম্বর ২০০১), The number e, The MacTutor History of Mathematics archive, সংগ্রহের তারিখ ২০০৯-০২-০২উদ্ধৃতি টেমপ্লেট ইংরেজি প্যারামিটার ব্যবহার করেছে (link)
6. Cajori, Florian (১৯৯১), A History of Mathematics (5th সংস্করণ), Providence, RI: AMS Bookstore, আইএসবিএন 978-0-8218-2102-2উদ্ধৃতি টেমপ্লেট ইংরেজি প্যারামিটার ব্যবহার করেছে (link) , p. 152
7. Hobson, Ernest William (১৯১৪)। John Napier and the invention of logarithms, 1614; a lecture। University of California Libraries। Cambridge : University Press।