دالة تكعيبية

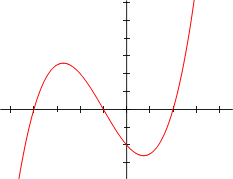
في الرياضيات وبالتحديد في الجبر، الدالة التكعيبية (بالإنجليزية: Cubic function) هي دالة رياضية لها الشكل التالي:

${\displaystyle f(x)=ax^{3}+bx^{2}+cx+d\,}$

دالة تكعيبية

معلومات عامة

صنف فرعي من	دالة كثيرة الحدود
الاستعمال	track transition curve [الإنجليزية]
تعريف الصيغة	${\displaystyle f(x)=ax^{3}+bx^{2}+cx+d,\quad x\in \mathbb {R} }$
له ميزة	درجة متعددة حدود

دالة تربيعية

دالة رباعية

تعديل - تعديل مصدري - تعديل ويكي بيانات

  ميّز عن معادلة تكعيبية.

مخطط الدالة التكعيبية ${\displaystyle f(x)=x^{3}+2x^{2}-5x-6}$، ذات ثلاث جذور حقيقية. جذور الدالة هي عند تقاطع المخطط مع محور السينات x.

حيث a لا يساوي الصفر.^[1] أو هي متعددة حدود من الدرجة الثالثة.

مشتق الدالة التكعيبية هي دالة تربيعية، وتكامل الدالة التكعيبية هي دالة من الدرجة الرابعة.

الصيغة ${\displaystyle f(x)=0\,}$ تسمى معادلة تكعيبية أو معادلة من الدرجة الثالثة :

${\displaystyle ax^{3}+bx^{2}+cx+d=0\,}$

حيث :${\displaystyle a\neq 0\,}$. إذا كانت a = 0, فتصبح معادلة تربيعية. أما إذا كان a و b مساويين للصفر، فإن المعادلة تصير خطية. عادة، تكون${\displaystyle a,b,c,d\,}$ أعدادا صحيحة.

إذا كانت كل معاملات الدالة التكعيبية أعدادا حقيقية، فإن للمعادلة على الأقل حلا حقيقيا (هذه الخاصية صحيحة بالنسبة لجميع متعددات الحدود ذات درجة فردية).

كل جذور المعادلات التكعيبية يمكن أن توجد جبريا. هذه الخاصية صحيحة أيضا بالنسبة إلى المعادلات التربيعية وتبقى صحيحة أيضا بالنسبة إلى المعادلات الرباعية ولكنها تصير خاطئة عندما يتعلق الأمر بمتعددات الحدود ذات الدرجة الخامسة وما فوق، أخذا بعين الاعتبار مبرهنة أبيل-روفيني. يمكن أيضا أن يتم ايجاد الجذور باستعمال الحساب المثلثي. مقابل ذلك يمكن أن يُقترب من الچذور باستعمال خوارزمية إيجاد جذور دالة، طريقة نيوتن مثالا على ذلك.

لا يفترض في معاملات المعادلة من الدرجة الثالثة أن تكون أعدادا مركبة. كل ما يلي يبقى صحيحا عندما تنتمي المعاملات إلى حقل ما محدده يساوي الصفر أي يتجاوز الثلاثة. جذور المعادلات من الدرجة الثالثة لا تنتمي حتما إلى نفس الحقل الذي تنتمي إليه معاملات هذه المعادلة. على سبيل المثال، قد يتم ايجاد معادلة من الدرجة الثالثة معاملاتها أعداد جذرية وجذورها ليست جذرية وليست حتى حقيقية بل هن جذور مركبة.

التاريخ

المقالة الرئيسة: معادلة تكعيبية § تاريخ

النقط الحرجة ونقطة الانعطاف لدالة تكعيبية

النقط الحرجة لدالة هن تلك القيم ل x حيث يكون انحناء الدالة مساويا للصفر. النقط الحرجة لدالة تكعيبية معرفة كما يلي f(x) = ax³ + bx² + cx + d من النقط اللائي يحققن المعادلة التالية:

${\displaystyle 3ax^{2}+2bx+c=0.}$

الحلحلة العامة لدالة تكعيبية معاملاتها أعداد حقيقية

المقالة الرئيسة: معادلة تكعيبية

استيفاء تكعيبي

المقالة الرئيسة: استيفاء شريحة

لتكن دالة قيمتها معروفة عند نقطتين اثنتين مختلفتين كما هو معروف أيضا قيمة اشتقاق هذه الدالة عند هاتين النقطتين. هناك دالة تكعيبية وحيدة تحقق هذه الشروط الأربعة. وتسمى بمنحنى هيرميت التكعيبي، نسبة إلى عالم الرياضيات الفرنسي شارل هيرمت.

انظر أيضا

• معادلة من الدرجة الأولى
• معادلة حدودية
• التكامل الوظيفي