التحليل التوافيقي[1] أو الرياضيات التوافيقية[2] أو التوافيقيات[3][4] (بالإنجليزية: Combinatorics أو Combinatorial analysis) هي أحد فروع الرياضيات التي تدرس البُنى المتقطعة المنتهية والقابلة للعد. تتضمن التركيبات عدّ العناصر في المجموعات، مع تحديد ما إذا كانت تتوافق مع المعايير المطلوبة، وكذلك دراسة بناء وتحليل الكائنات التي تحقق هذه المعايير (كما في التصميم التوافيقي ونظرية الماترويد)، يهتم هذا العلم أيضاً بإيجاد الكائنات الأكبر أو الأصغر أو الأفضل (فيما يعرف بالتوافيقيات الحجمية والتوافيقيات التحسينية). ودراسة الهيكل التركيبي الظاهر في محتوى جبري، أو تطبيق تقنيات الجبر لحل مسائل التوافيقيات (التوافيقيات الجبرية [الإنجليزية]).
| صنف فرعي من | |
|---|---|
| جزء من | |
| سُمِّي باسم | |
| يدرس | |
| نظام تصنيف حوسبة رابطة مكائن الحوسبة (2012) |
10003625  |
التاريخ
ظهرت مفاهيم التوافيقيات الابتدائية منذ القدم. في القرن السادس قبل الميلاد صرح ساسروتا سامهيتا طبيب هندي قديم، أنه بالإمكان صناعة 63 مذاقا مختلفا انطلاقا من ست توابل مختلفة.
انظر أعداد شرودر.
مقاربات التوافيقياتوفروعها
التوافيقيات التعدادية
انظر إلى عدد فيبوناتشي.
نظرية التجزآت
في نظرية الأعداد وفي التوافيقيات، تجزئة عدد طبيعي هي طريقة لكتابة هذا العدد على شكل مجموع أعداد طبيعية. مجموعان يختلفان فقط في ترتيب حدودهما، يعتبران نفس المجموع. على سبيل المثال، يكتب 4 على شكل خمسة مجاميع مختلفة وهي:
- 4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1.
نظرية المخططات
نظرية المخططات هي نظرية في الرياضيات وعلوم الحاسب، تدرس خواص المخططات حيث يتم تمثيل مجموعة كائنات تدعى رؤوسا، ترتبط ببعضها بأضلاع وتدعى أحيانا أقواسا، يمكن أن تكون موجهة أي مزودة باتجاه (تستخدم الاسهم بدل الأضلاع) أو بدون اتجاه (أضلاع فقط). التمثيل لهذا المخطط يكون على الورق بمجموعة نقاط تمثل الرؤوس متصلة بخطوط هي حروف (أضلاع أو أسهم) المخطط.
تُمكن الاستعانة بالمخططات من حلحلة الكثير من المشاكل العملية، فمثلا بنية موسوعة ويكيبيديا يمكن تمثيلها بمخطط رؤوسه هي أسماء المقالات ونقوم برسم خط موجه بين مقالتين من أ إلى ب إذا كانت المقالة أ تحوي رابطا إلى المقالة ب. تطبيقات هذه النظرية واسعة جدا ولحل مشاكلها يستخدم الحاسوب بشكل واسع. لذلك تهتم علوم الحاسوب بتصميم خوارزميات لنظرية المخططات حيث يمكن معالجة أي مخطط لتمييز خصائصه واستخلاص المعلومات منه.
تعتبر المخططات كائنات أساسية في دراسة التوافيقيات.
الهندسة المنتهية
الهندسة المنتهية هي أي نظام هندسي رياضي يحوي عددا منتهيا (محددا) من النقاط. على سبيل المثال، الهندسة الإقليدية هي هندسة غير منتهية، حيث أن المستقيم الإقليدي يحتوي عددا لا نهائيا من النقاط. من الممكن للهندسة المنتهية أن تمتلك عددا منتهيا من الأبعاد.
نظرية الترتيب
نظرية الترتيب هي فرع من الرياضيات يهتم بدراسة الأنواع المختلفة من العلاقات الثنائية التي تعطي انطباعا حسّياً عن فكرة ترتيبها موفرة بنية يمكن القول من خلالها متى يكون الشيء «أقل من» أو «يسبق» الآخر.
تدرس نظرية الترتيب مختلف أنواع العلاقات الثنائية بين العناصر الرياضية المختلفة التي ترمز ترتيب هذه العناصر.
التوافيقيات الاحتمالية
مبادئ العد الأساسية
مبدأ الضرب
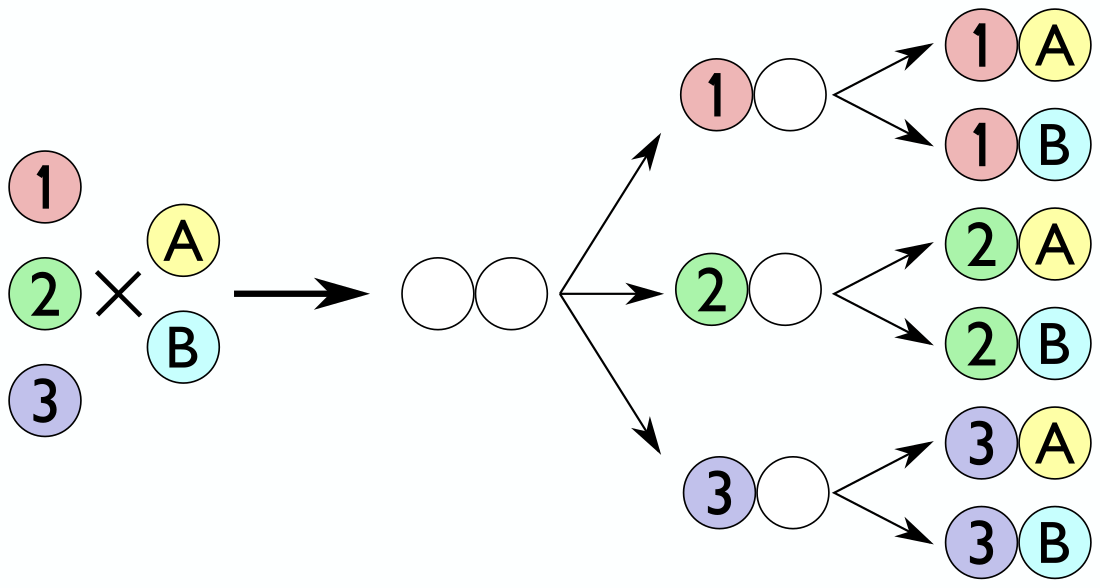
إذا كان لدينا مجموعتان مختلفتان وعدد الإمكانيات للاختيار من المجموعة الأولى هو N وعدد الإمكانيات للاختيار من المجموعة الثانية هو M، فإن عدد الإمكانيات للاختيار من المجموعة الأولى و المجموعة الثانية هو .
مثال: لدى منال 5 تنانير و 7 قمصان. في كل مرة تخرج فيها من البيت ترتدي قميصا وتنورة. كم إمكانية مختلفة توجد لمنال لاختيار قميص و تنورة؟. الإجابة: حسب قانون الضرب إمكانية مختلفة.
مراجع
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
